如何在 sas 中计算偏度和峰度
在统计学中,偏度和峰度是测量分布形状的两种方法。
偏度衡量分布的不对称性。
- 负偏度表示尾部位于分布的左侧。
- 正偏度表示尾部位于分布的右侧。
- 值为零表示分布不存在不对称性,这意味着分布完全对称。
峰度衡量与正态分布相比,分布是重尾还是轻尾。
- 正态分布的峰度为 0。
- 如果给定分布的峰度小于 0,则称其为playkurtic ,这意味着与正态分布相比,它往往会产生越来越少的极端异常值。
- 如果给定分布的峰度大于 0,则称为峰态分布,这意味着它往往会比正态分布产生更多的异常值。
要计算 SAS 中变量的偏度和峰度,可以使用PROC MEANS中的SKEWNESS和KURTOSIS语句。
以下示例展示了如何在实践中使用这些说明。
示例:计算 SAS 中的偏度和峰度
假设我们在 SAS 中有以下数据集,其中包含有关各种篮球运动员的信息:
/*create dataset*/ data my_data; input team $points assists; datalines ; At 10 2 At 17 5 At 17 6 At 18 3 At 15 0 B 10 2 B 14 5 B 13 4 B 29 0 B 25 2 C 12 1 C 30 1 C 34 3 C 12 4 C 11 7 ; run ; /*view dataset*/ proc print data =my_data;
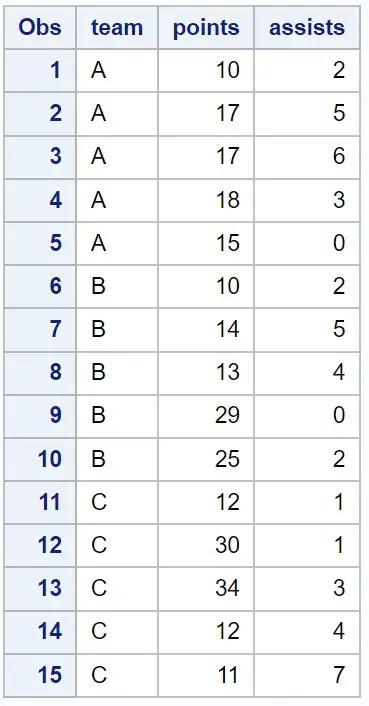
我们可以将PROC MEANS与SKEWNESS和KURTOSIS语句结合使用来计算数据集中每个数值变量的偏度和峰度:
/*calculate skewness and kurtosis for each numeric variable*/ proc means data =my_data SKEWNESS KURTOSIS ; run ;
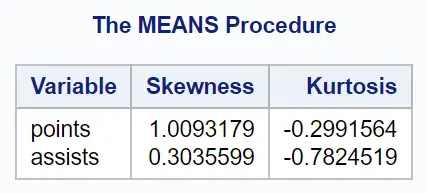
输出表显示数据集中每个数值变量的偏度和峰度值:
(1) 积分
- 点变量的偏度为1.009 。由于该值大于 0,因此意味着尾部位于分布的右侧。
- 点变量的峰度为-0.299 。由于该值小于 0,因此意味着该分布比正态分布的异常值和极值稍少。
(2)帮助
- 助攻变量的偏度为0.304 。由于该值大于 0,因此意味着尾部位于分布的右侧。
- 支持变量的峰度为-0.782 。由于该值小于 0,因此意味着该分布比正态分布具有更少的异常值和更少的极值。
要可视化数据集中每个数值变量的值分布,可以使用PROC UNIVARIATE为点变量和辅助变量创建直方图:
/*create histograms for points and assists variables*/
proc univariate data =my_data;
var points assists;
histogram points assists;
run ;
这会生成以下点变量的直方图:
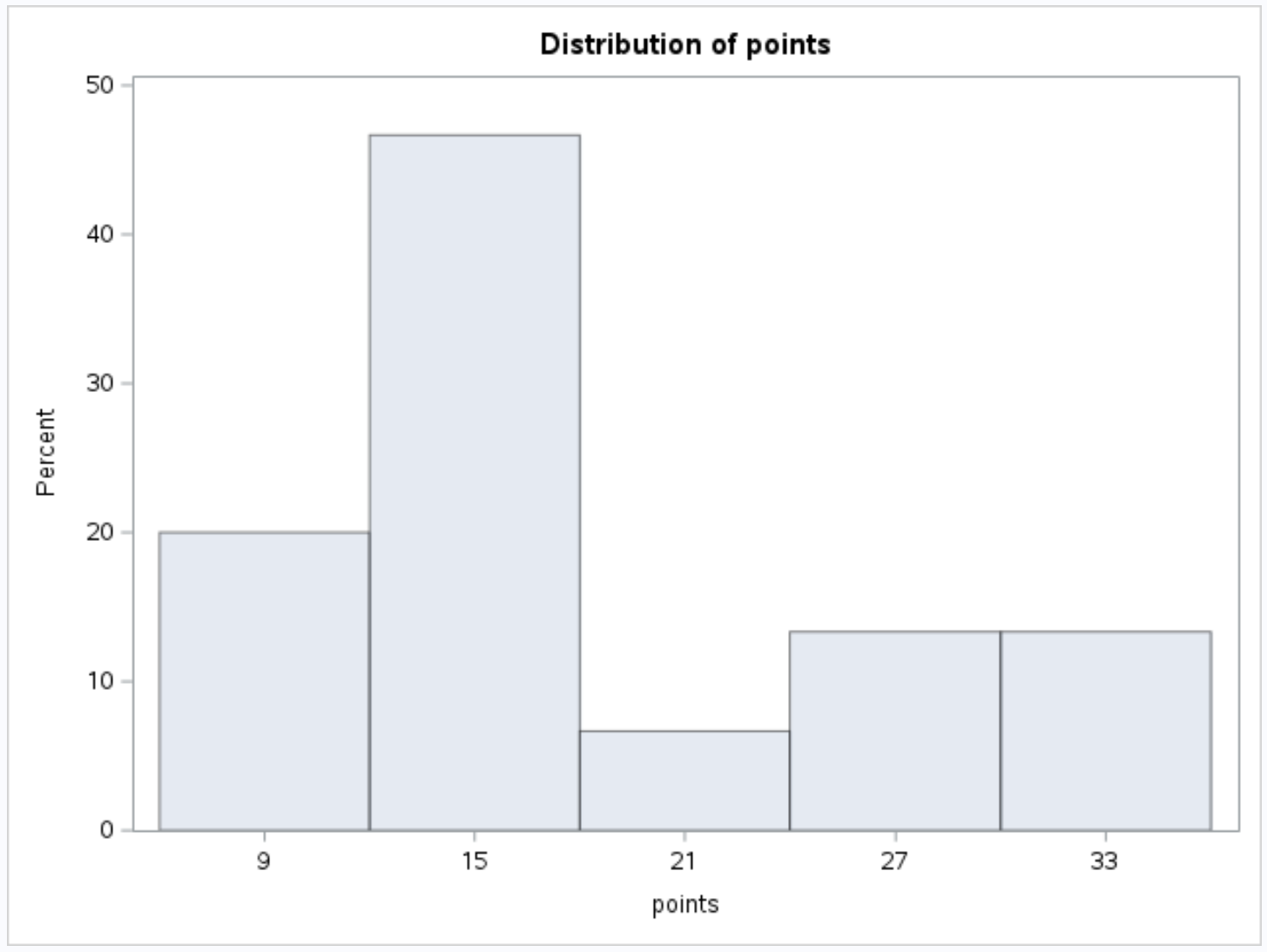
以及辅助变量的以下直方图:
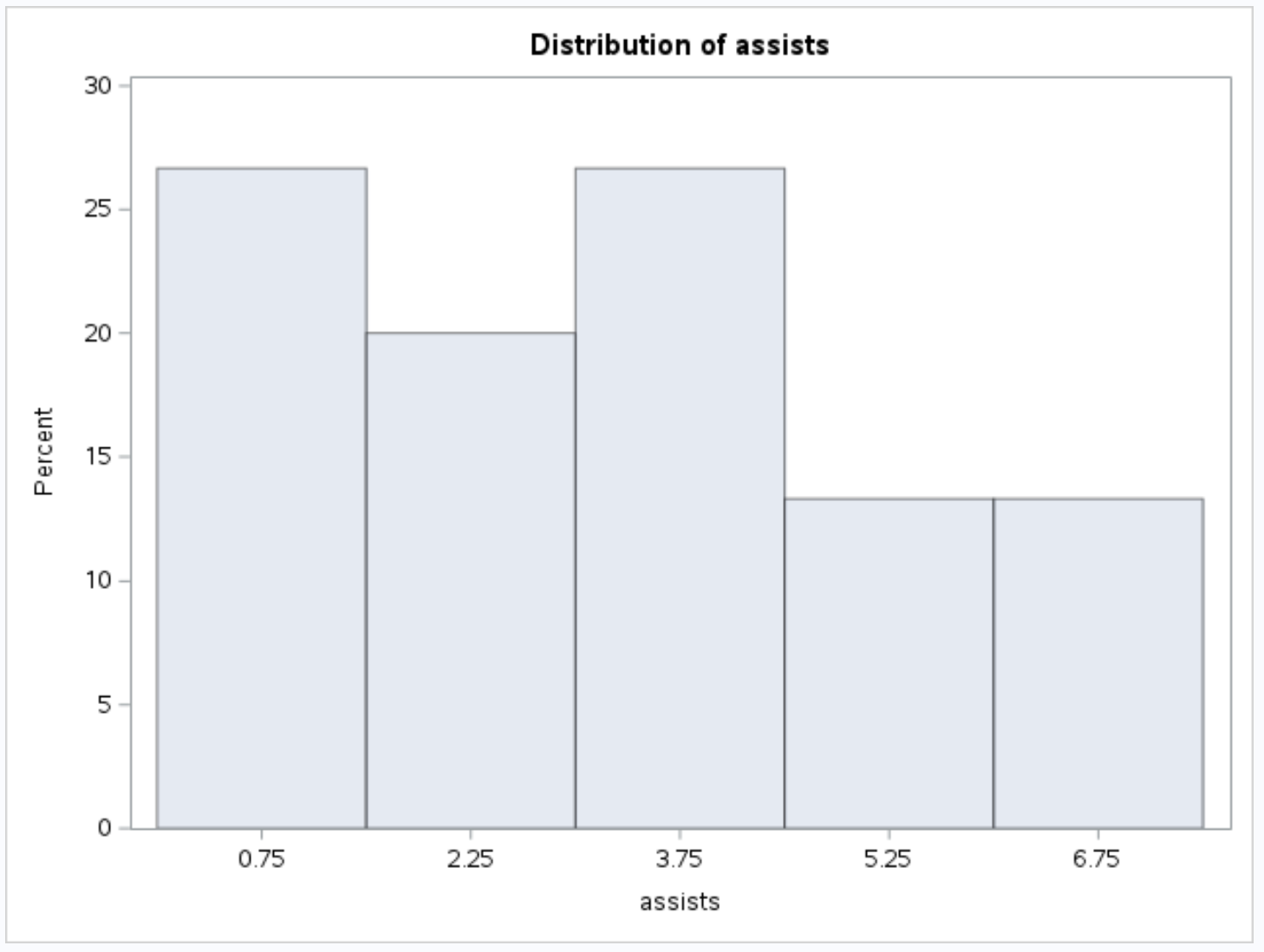
其他资源
以下教程解释了如何在 SAS 中执行其他常见任务: