如何在 excel 中计算 z 分数
在统计学中, z 分数告诉我们某个值与平均值的标准差有多少。我们使用以下公式来计算 z 分数:
z = (X – μ) / σ
金子:
- X 是单个原始数据值
- μ 是数据集的平均值
- σ 是数据集的标准差
本教程介绍如何在 Excel 中计算原始数据值的 z 分数。
如何在 Excel 中计算 Z 分数
假设我们有以下数据集,并且想要找到每个原始数据值的 z 分数:
我们可以执行以下步骤来执行此操作。
步骤 1:计算数据集的平均值和标准差。
首先,我们需要找到数据集的平均值和标准差。以下公式显示了如何执行此操作:
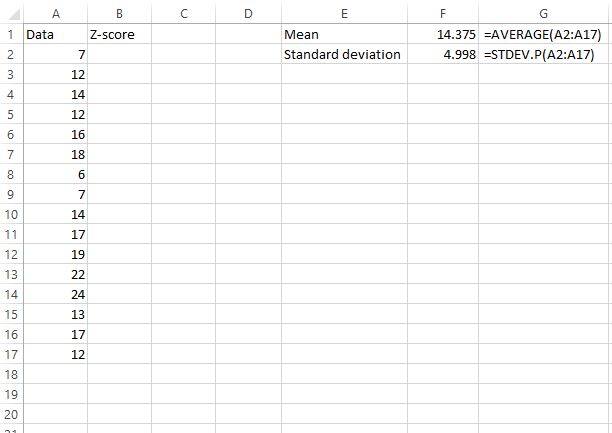
平均值为14.375 ,标准差为4.998 。
步骤 2:查找第一个原始数据值的 z 分数。
接下来,我们将使用公式z = (X – μ) / σ 找到第一个原始数据值的 z 分数。
单元格 C2 显示了我们用于计算单元格 B2 中 z 值的公式。
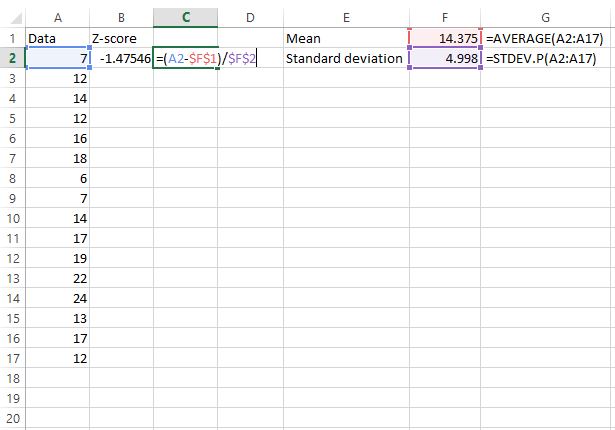
步骤 3:查找所有剩余值的 z 分数。
现在我们已经找到了数据集中第一个值的 z 分数,我们可以简单地将单元格 B2 中使用的公式复制到其余数据值中。我们可以通过突出显示整个 z 分数列来做到这一点,从我们已经计算的第一个 z 分数开始:
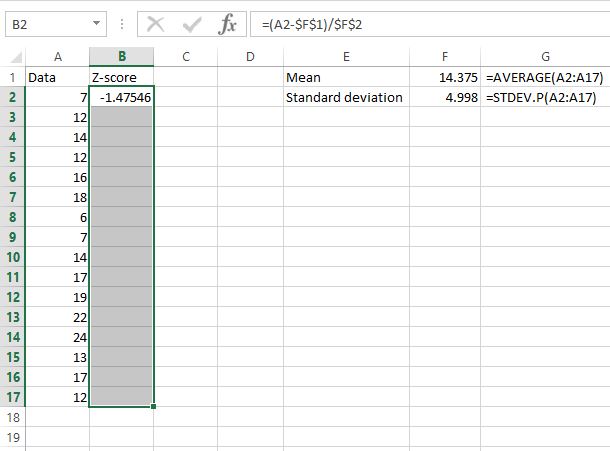
接下来,按Ctrl+D 。这会将公式从第一个单元格复制到其下面的所有单元格。
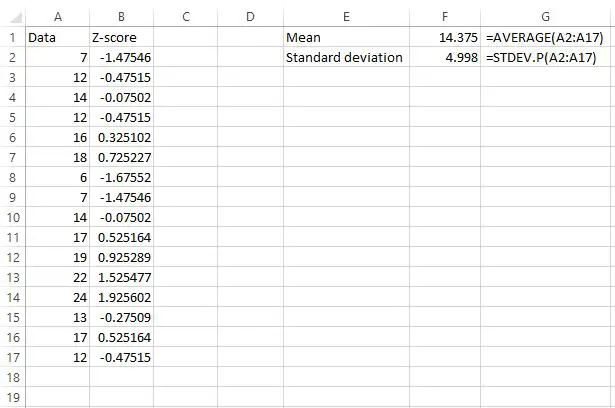
我们现在已经找到了每个原始数据值的 z 分数。
如何在 Excel 中解释 Z 分数
请记住, z 分数只是告诉我们某个值与平均值的标准差有多少。
z 分数可以是正数、负数或零。
正 z 分数表示特定值高于平均值,负 z 分数表示特定值低于平均值,z 分数为零表示特定值等于平均值。
在我们的示例中,我们发现平均值为14.375 ,标准差为4.998 。
因此,我们数据集中的第一个值为 7,其 z 分数为 (7-14.375) / 4.998 = -1.47546 。这意味着值“7”比平均值低-1.47545 个标准差。
我们数据中的下一个值 12 的 z 得分为 (12-14.375) / 4.998 = -0.47515 。这意味着值“12”比平均值低-0.47515 个标准差。

值离平均值越远,该值的 z 分数绝对值就越高。
例如,值 7 比值 12 距离平均值 (14.375) 更远,这解释了为什么 7 的 z 分数的绝对值更大。
其他资源
以下文章提供了有关如何在 Excel 中使用 z 分数的更多信息: