四分位距 (iqr) 是否受异常值影响?
在统计学中,我们经常想知道值在分布中“分散”的范围有多大。
衡量分布的一种流行方法是四分位数间距,它的计算方法是数据集的第一个四分位数和第三个四分位数之间的差。四分位数只是将数据集分为四个相等部分的值。
示例:四分位距的计算
以下示例显示如何计算给定数据集的四分位数范围:
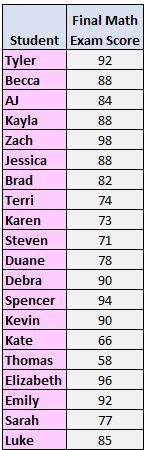
步骤一:将数值从小到大排列。
58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98
2. 求中位数。
58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98
在本例中,中位数介于 85 到 88 之间。
3. 中位数将数据集分为两半。下半部分的中位数是下四分位数,上半部分的中位数是上四分位数:
58, 66, 71 , 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98
4. 计算四分位距。
在这种情况下,第一个四分位数是数据集下半部分中间两个值的平均值(75.5),第三个四分位数是数据集上半部分中间两个值的平均值(91)。
所以四分位数范围是 91 – 75.5 = 15.5
四分位数范围不受异常值的影响
人们在计算数据集的“分布”时更喜欢使用四分位距 (IQR) 的原因之一是它对异常值具有鲁棒性。由于 IQR 只是数据值的中间 50% 范围,因此它不受极端异常值的影响。
为了证明这一点,请考虑以下数据集:
[1, 4, 8, 11, 13, 17, 17, 20]
以下是该数据集的不同传播指标:
- 四分位数间距:11
- 范围:19
- 标准差:6.26
- 差异:39.23
现在考虑相同的数据集,但添加了极端异常值:
[1, 4, 8, 11, 13, 17, 17, 20, 150 ]
以下是该数据集的不同传播指标:
- 四分位数间距:12.5
- 范围:149
- 标准差:43.96
- 点差:1,932.84
请注意四分位数范围仅略有变化,从 11 到 12.5。然而,所有其他分散度指标都发生了巨大变化。
这表明四分位距不像其他离散度度量那样受到异常值的影响。因此,它是衡量任何分布中中间 50% 值的分布的可靠方法。
进一步阅读:
色散测量
四分位距计算器