如何在stata中获取预测值和残差

线性回归是一种我们可以用来理解一个或多个解释变量与响应变量之间关系的方法。

当我们对数据集执行线性回归时，我们最终会得到一个回归方程，在给定解释变量的值的情况下，该方程可用于预测响应变量的值。

然后我们可以测量预测值和实际值之间的差异，以获得每个预测的残差。这有助于我们了解回归模型预测响应值的效果。

本教程介绍如何在 Stata 中获取回归模型的预测值和残差。

示例：如何获取预测值和残差

在本例中，我们将使用名为auto 的内置 Stata 数据集。我们将使用mpg和位移作为解释变量，使用价格作为响应变量。

使用以下步骤执行线性回归，然后获得回归模型的预测值和残差。

步骤1：加载并显示数据。

首先，我们将使用以下命令加载数据：

系统自动使用

接下来，我们将使用以下命令快速汇总数据：

总结一下

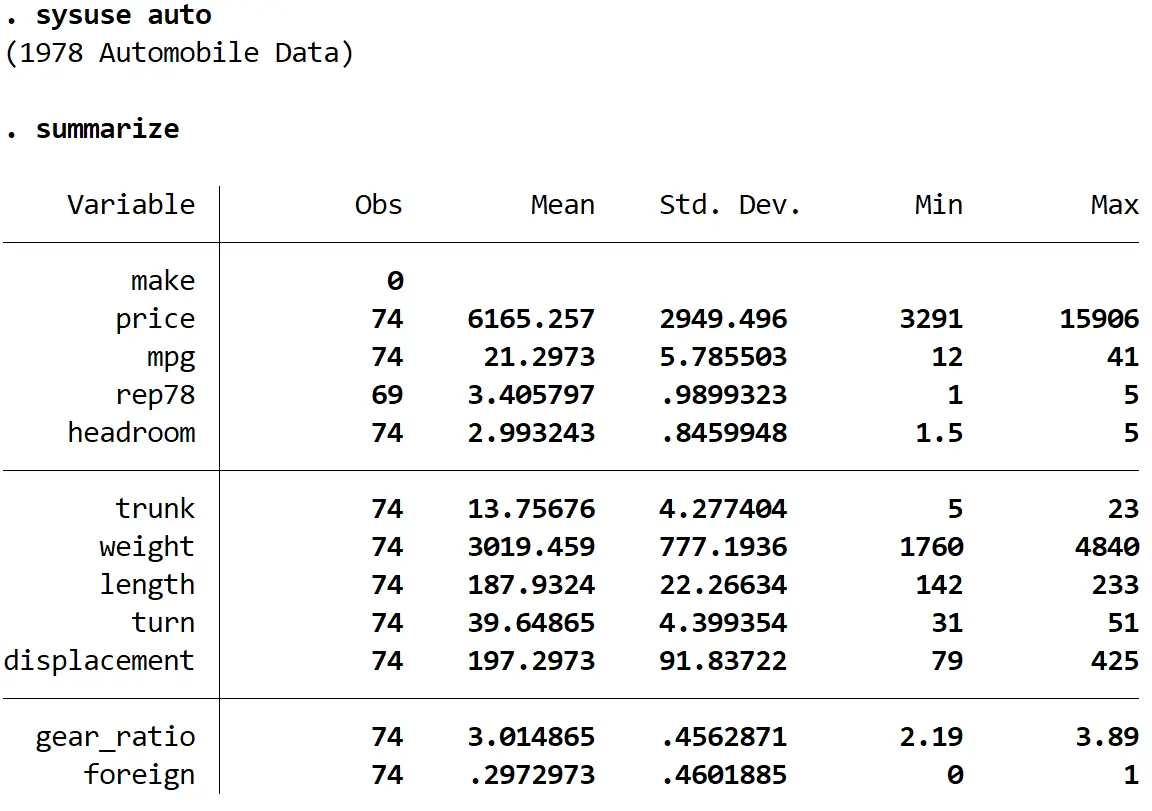
步骤 2：拟合回归模型。

接下来，我们将使用以下命令来拟合回归模型：

回归价格 mpg 排量

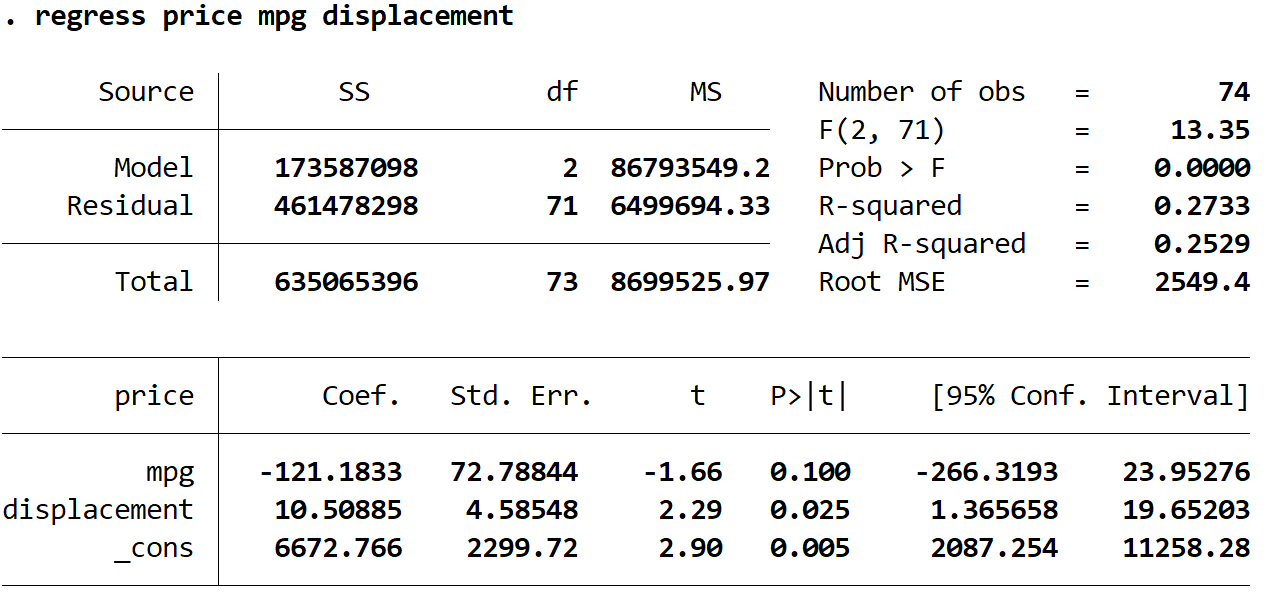
估计回归方程为：

预估价格 = 6672.766 -121.1833*(mpg) + 10.50885*(排量)

步骤3：获取预测值。

我们可以通过使用预测命令来获取预测值，并将这些值存储在我们希望命名的变量中。在本例中，我们将使用名称pred_price ：

预测 pred_price

我们可以使用list命令并排显示实际价格和预测价格。总共有 74 个预测值，但我们只会使用in 1/10命令显示前 10 个：

标价 pred_price 为 1/10

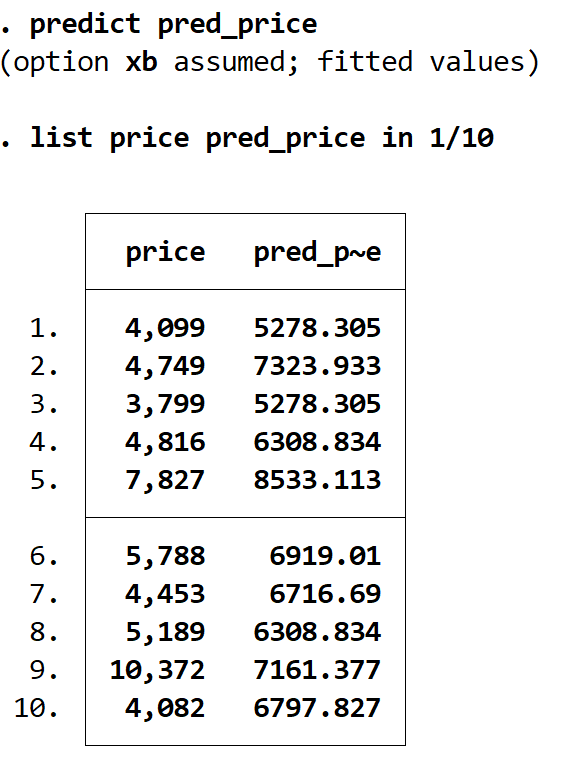
第四步：获取残留物。

我们可以通过使用residuals命令来获得每个预测的残差，并将这些值存储在一个我们想要命名的变量中。在本例中，我们将使用名称resid_price ：

预测 Residence_price、残差

我们可以再次使用list命令并排显示实际价格、预期价格和残差：

标价 pred_price resid_price 为 1/10

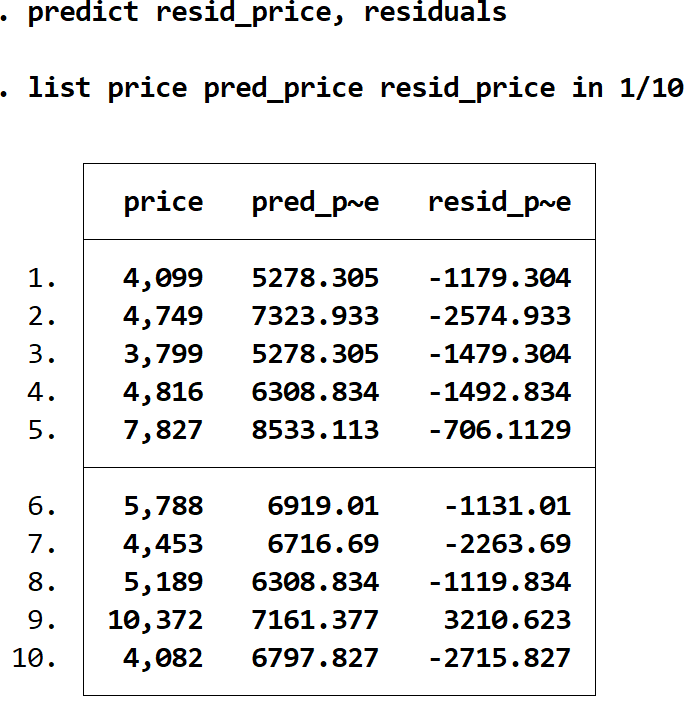
步骤 5：创建预测值与残差的关系图。

最后，我们可以创建一个散点图来可视化预测值和残差之间的关系：

分散 驻留价格 预测价格

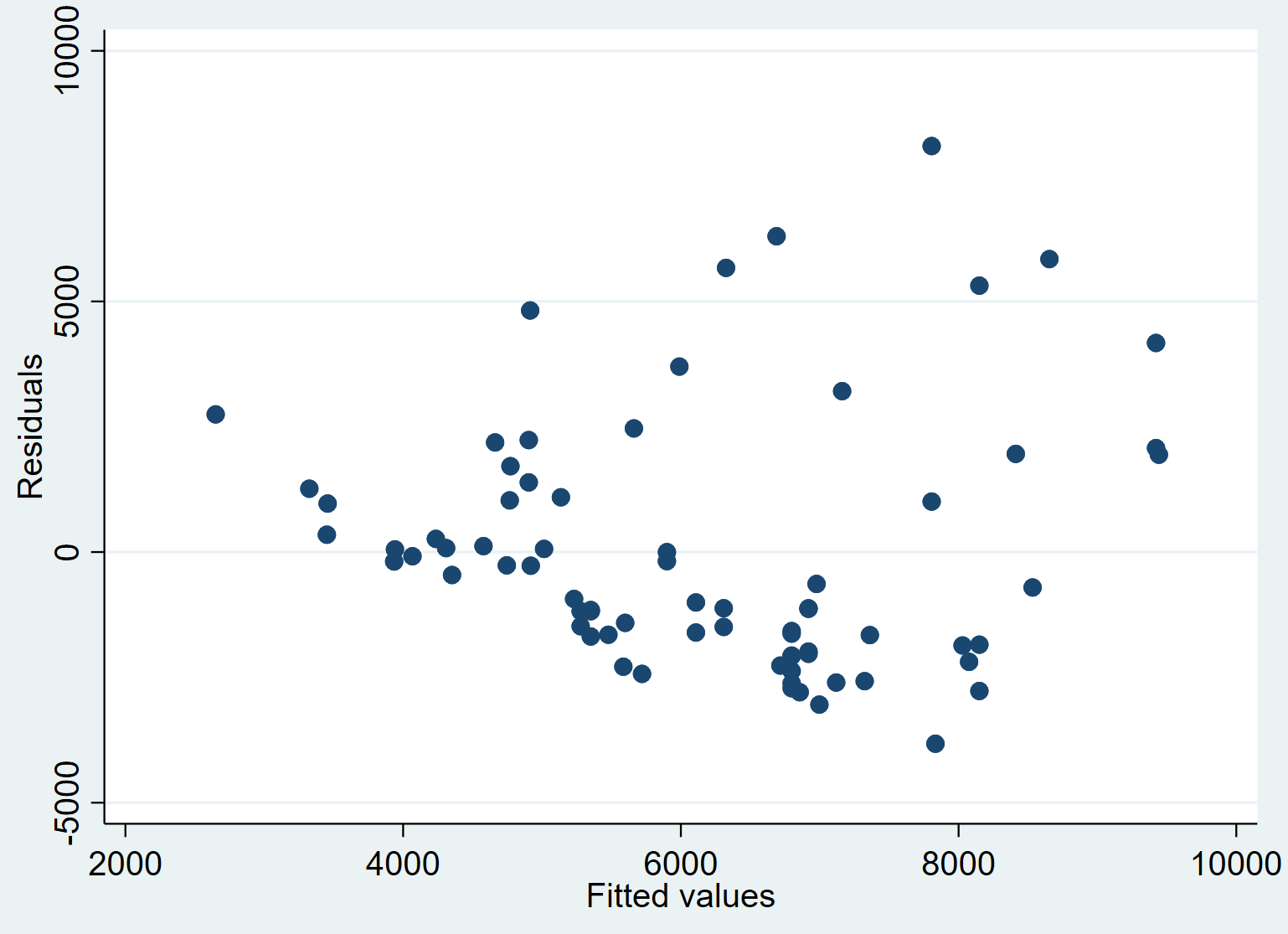
我们可以看到，平均而言，残差随着拟合值的增加而趋于增加。当残差分布在每个响应水平上不恒定时，这可能是异方差的标志。

我们可以使用Breusch-Pagan 检验正式检验异方差性，并使用稳健的标准误差来解决这个问题。