如何在 stata 中进行分位数回归

线性回归是一种我们可以用来理解一个或多个解释变量与响应变量之间关系的方法。

通常，当我们进行线性回归时，我们希望根据解释变量的值来估计响应变量的平均值。但我们可以估计中位数，或 0.25 百分位，或 0.90 百分位，或我们想要的任何其他百分位。

这就是分位数回归的用武之地。与线性普通回归类似，分位数回归创建一个回归方程，该方程根据解释变量的值预测响应变量的某个值（例如中位数、0.25 百分位数、0.90 百分位数等）。

本教程介绍如何在 Stata 中执行分位数回归。

示例：Stata 中的分位数回归

在本例中，我们将使用名为auto 的内置 Stata 数据集。我们首先将使用体重作为预测变量，将英里数作为响应变量来拟合线性回归模型。这将告诉我们基于汽车重量的平均预期英里数。接下来，我们将拟合分位数回归模型，根据汽车的重量来预测汽车的 0.90 mpg 百分位。

步骤1：加载并显示数据。

使用以下命令加载数据：

系统自动使用

使用以下命令获取 mpg 和体重变量的摘要：

总结 mpg 重量

步骤 2：执行简单线性回归。

使用以下命令执行简单的线性回归，使用体重作为解释变量，mpg 作为响应变量：

将体重回归为英里/加仑

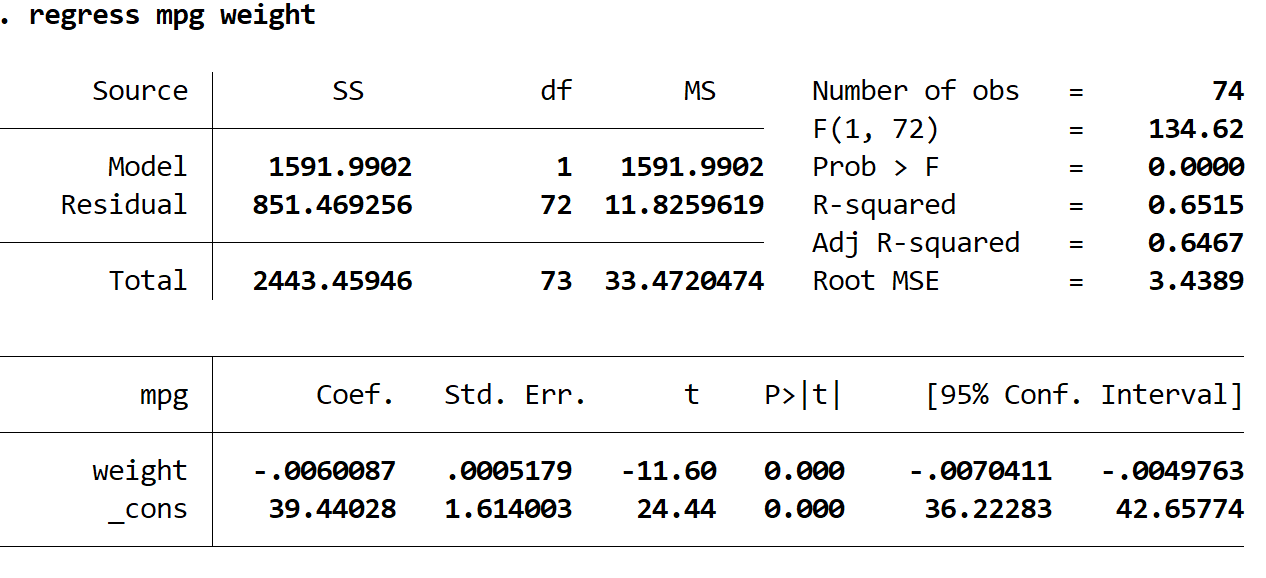
从输出表中我们可以看到估计的回归方程为：

预测英里/加仑 = 39.44028 – 0.0060087*（体重）

我们可以使用这个方程来计算汽车在给定重量的情况下的估计平均英里数。例如，一辆重 4,000 磅的汽车估计其 mpg 为 15,405：

预测英里/加仑 = 39.44028 – 0.0060087*(4000) = 15.405

步骤 3：执行分位数回归。

接下来，我们执行分位数回归，以获得根据汽车重量估计的汽车燃油经济性的^{第 90 个}百分位数。

使用带有quantile(0.90)的qreg命令来执行此分位数回归：

重量 qreg mpg，分位数 (0.90)

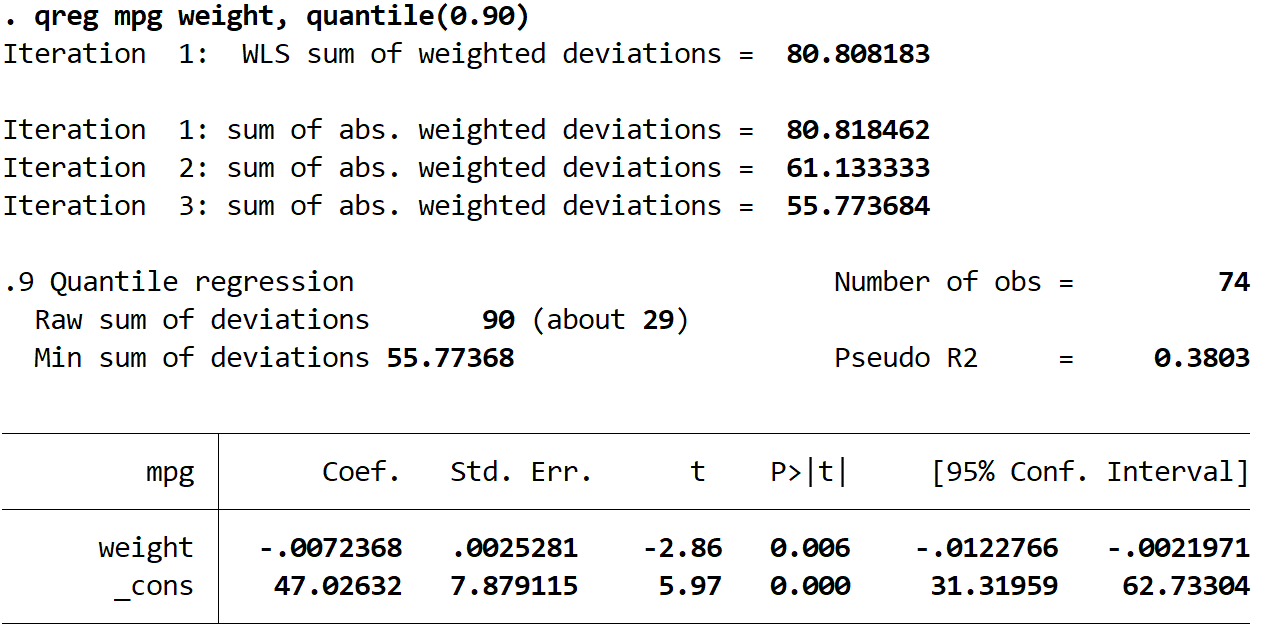
从输出表中我们可以看到估计的回归方程为：

^{第 90 个}百分位预测 mpg = 47.02632 – 0.0072368*（体重）

我们可以使用这个方程来找到估计值 考虑到其重量，汽车的 mpg 处于^{第 90 个}百分位数。例如，一辆重 4,000 磅的汽车的⁹⁰ % mpg 估计为 18,709：

^{第 90 个}百分位预测 mpg = 47.02632 – 0.0072368*(4,000) = 18.079

回想一下，我们之前的线性回归模型告诉我们，一辆重 4,000 磅的汽车的估计平均燃油经济性为 15,405 英里/加仑。因此，这个分位数回归模型告诉我们，一辆重 4,000 磅的汽车需要达到18,079英里/加仑才能进入该特定重量的所有汽车的^{第 90 个}百分位数，这是有道理的。

在 Stata 中同时进行多个分位数回归

还可以在 Stata 中同时执行多个分位数回归。例如，假设我们要同时估计^{第 25 个}百分位数、中位数（例如第^{50 个}百分位数）和第^{90 个}百分位数。

为此，我们可以使用sqreg命令和q()命令来指定要估计的分位数：

重量 mpg sqreg, q (0.25, 0.50, 0.90)

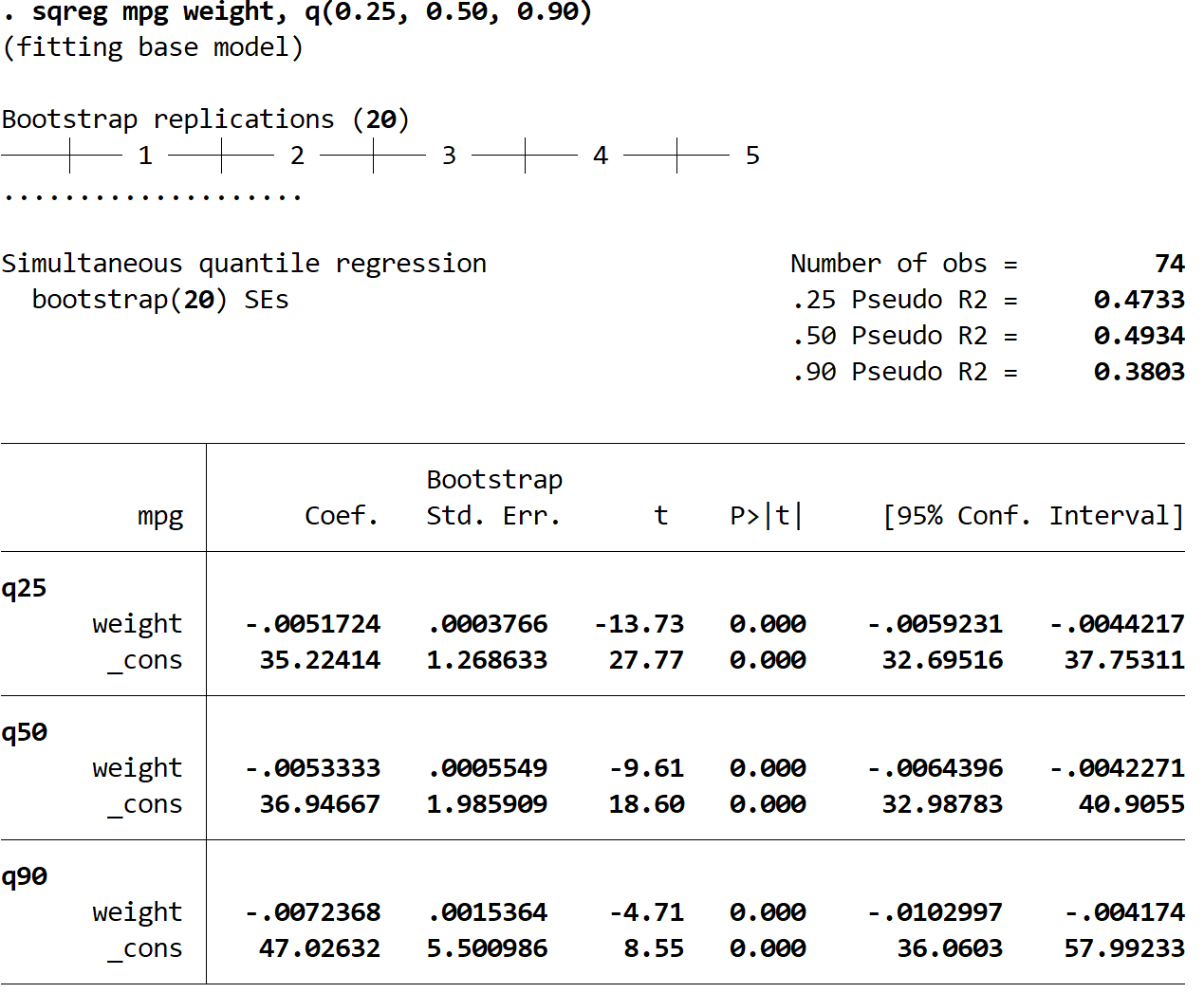
使用这个结果，我们可以构建每个分位数回归的估计回归方程：

(1)^{第 25 个}百分位预测 mpg = 35.22414 – 0.0051724*（体重）

(2)^{第 50 个}百分位预测 mpg = 36.94667 – 0.0053333*（体重）

(3) ⁹⁰ % 预测 mpg = 47.02632 – 0.0072368*（体重）

其他资源

如何在 Stata 中进行简单线性回归
如何在Stata中进行多元线性回归
如何在 Stata 中进行二次回归