如何在 ti-84 计算器上计算二项式概率

二项分布是所有统计中最常用的分布之一。本教程介绍如何在 TI-84 计算器上使用以下函数来计算二项式概率：

binompdf(n, p, x)返回与二项式 pdf 相关的概率。

binomcdf(n, p, x)返回与二项式 cdf 关联的累积概率。

金子：

• n = 试验次数
• p = 给定试验的成功概率
• x = 成功总数

在 TI-84 计算器上，可以通过按2nd然后按vars来访问这两个函数。这将带您进入DISTR屏幕，您可以在其中使用binompdf()和binomcdf() ：

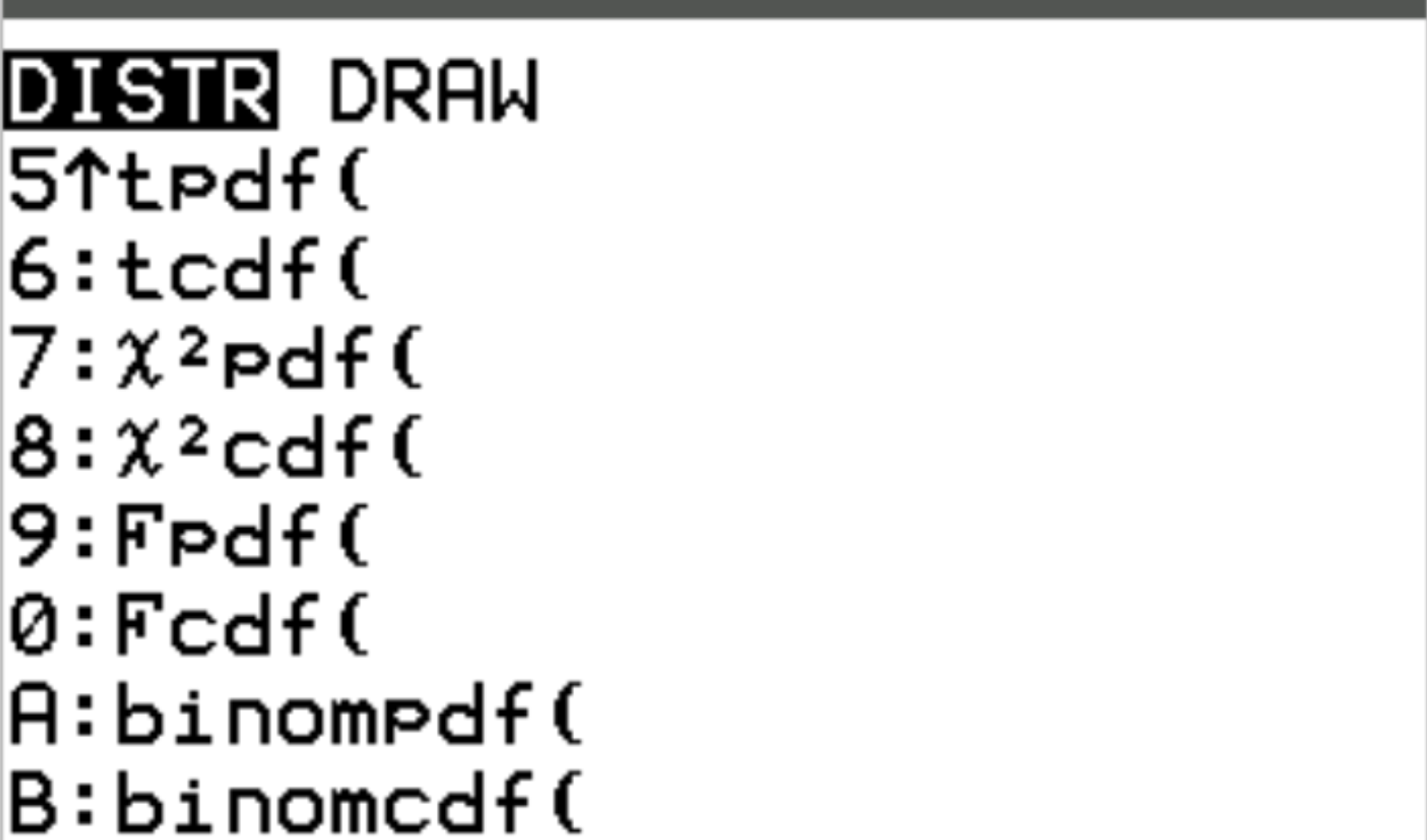
以下示例说明了如何使用这些函数来回答不同的问题。

示例 1：恰好 x 成功的二项式概率

问题：内森的罚球命中率为 60%。如果他罚球 12 次，他罚中 10 次的概率是多少？

答案：使用 binomialpdf(n, p, x) 函数：

二项式pdf(12, .60, 10) = 0.0639

示例 2：小于 x 成功的二项式概率

问题：内森的罚球命中率为 60%。如果他罚球 12 次，那么他罚球少于 10 次的概率是多少？

答案：使用binomialcdf(n, p, x-1)函数：

二项式cdf(12, .60, 9) = 0.9166

示例 3：至多 x 成功的二项式概率

问题：内森的罚球命中率为 60%。如果他罚球 12 次，他最多罚 10 球的概率是多少？

答案：使用binomialcdf(n, p, x)函数：

二项式cdf(12, .60, 10) = 0.9804

示例 4：超过 x 次成功的二项式概率

问题：内森的罚球命中率为 60%。如果他罚球 12 次，那么他罚球超过 10 次的概率是多少？

答案：使用函数1 – binomialcdf(n, p, x) ：

1 – 二项式cdf(12, .60, 10) = 0.0196

示例 5：至少 x 成功的二项式概率

问题：内森的罚球命中率为 60%。如果他罚球 12 次，那么他罚球超过 10 次的概率是多少？

答案：使用函数1 – binomialcdf(n, p, x-1) ：

1 – 二项式cdf(12, .60, 9) = 0.0834