如何在 excel 中应用切比雪夫定理

切比雪夫定理指出，对于任何大于 1 的数字 k，任何训练分布中至少有1 – 1/k ²的数据值位于与平均值的 k 个标准差之内。

例如，对于任何形状的分布，分布中至少 1 – 1/3 ² = 88.89% 的值将落在平均值的 3 个标准差范围内。

本教程演示了在 Excel 中应用切比雪夫定理的几个示例。

示例 1：使用切比雪夫定理确定对于均值为 50、标准差为 10 的数据集，值落在 30 到 70 之间的百分比是多少。

首先，确定k的值。我们可以通过确定平均值在 30 到 70 之间的标准差来做到这一点：

(30 – 平均值) / 标准差 = (30 – 50) / 10 = -20 / 10 = -2

(70 – 平均值) / 标准差 = (70 – 50) / 10 = 20 / 10 = 2

值 30 和 70 分别低于平均值和高于平均值 2 个标准差。所以， k = 2 。

然后，我们可以在 Excel 中使用以下公式来查找该数据集平均值的 2 个标准差范围内的值的最小百分比：

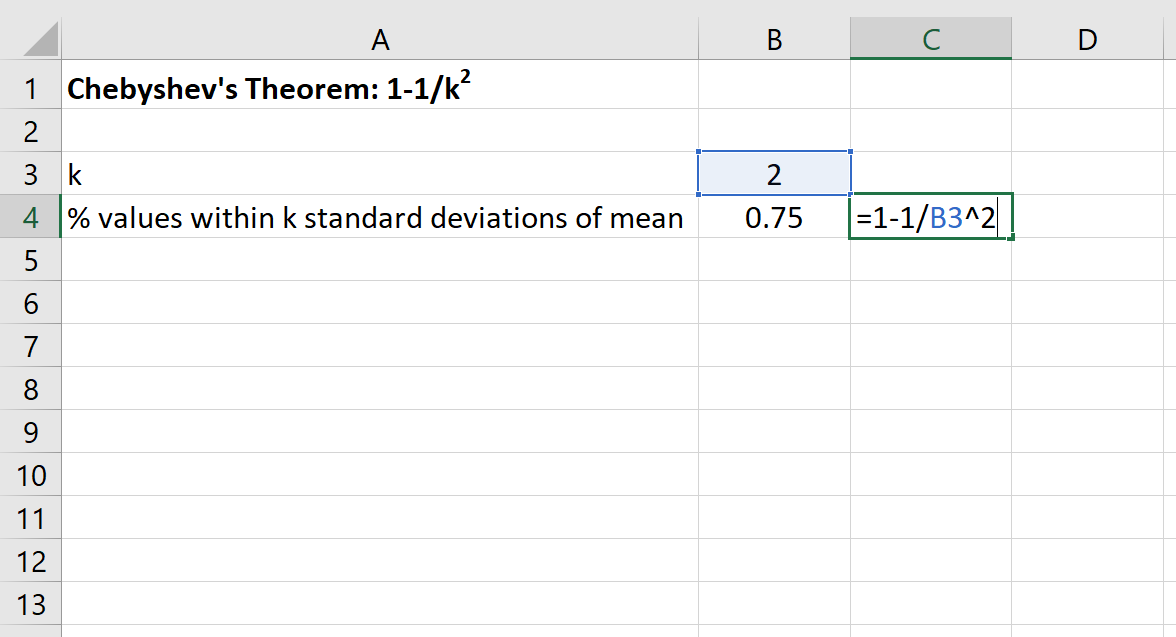
该数据集的 30 到 70 之间的值的百分比至少为 75% 。

示例 2：使用切比雪夫定理确定对于均值为 35、标准差为 5 的数据集，值落在 20 到 50 之间的百分比是多少。

首先，确定k的值。我们可以通过确定平均值在 20 到 50 之间的标准差有多少来做到这一点：

(20 – 平均值) / 标准差 = (20 – 35) / 5 = -15 / 5 = -3

(50 – 平均值) / 标准差 = (50 – 35) / 5 = 15 / 5 = 3

值 20 和 50 分别低于平均值和高于平均值 3 个标准差。所以， k = 3 。

然后，我们可以在 Excel 中使用以下公式来查找该数据集平均值的 3 个标准差范围内的值的最小百分比：

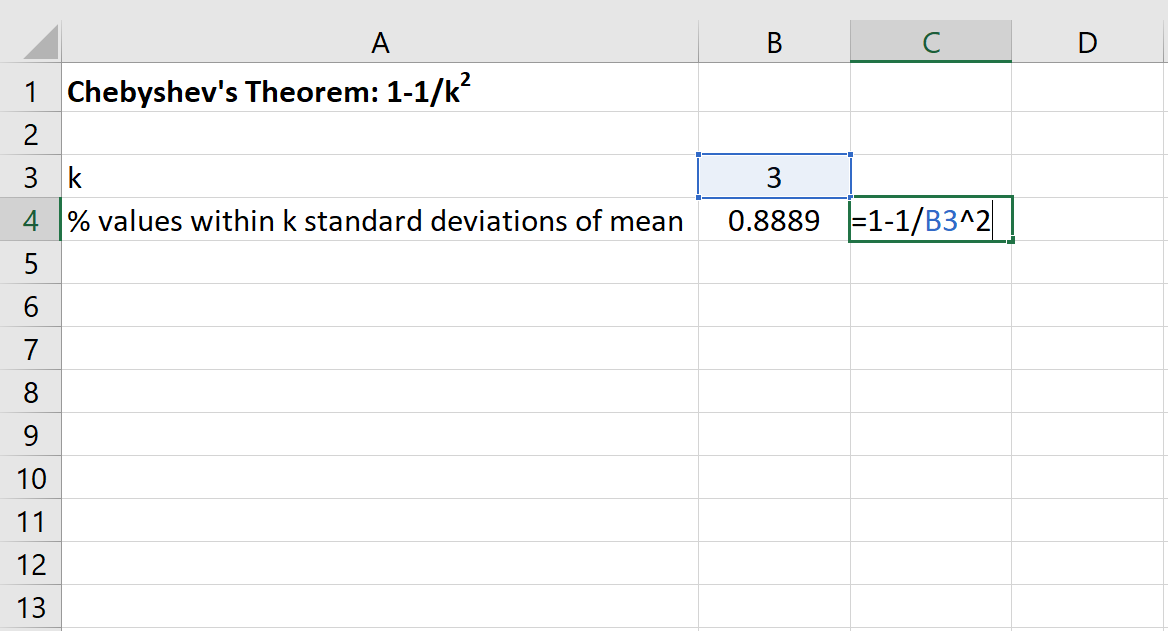
该数据集的 20 到 50 之间的值的百分比至少为 88.89% 。

示例 3：使用切比雪夫定理确定对于均值为 100、标准差为 5 的数据集，值落在 80 到 120 之间的百分比是多少。

首先，确定k的值。我们可以通过确定平均值在 80 到 120 之间的标准差来做到这一点：

(80 – 平均值) / 标准差 = (80 – 100) / 5 = -20 / 5 = -4

(120 – 平均值) / 标准差 = (120 – 100) / 5 = 20 / 5 = 4

值 80 和 120 分别低于平均值和高于平均值 4 个标准差。所以， k = 4 。

然后，我们可以在 Excel 中使用以下公式来查找该数据集平均值的 4 个标准差范围内的值的最小百分比：

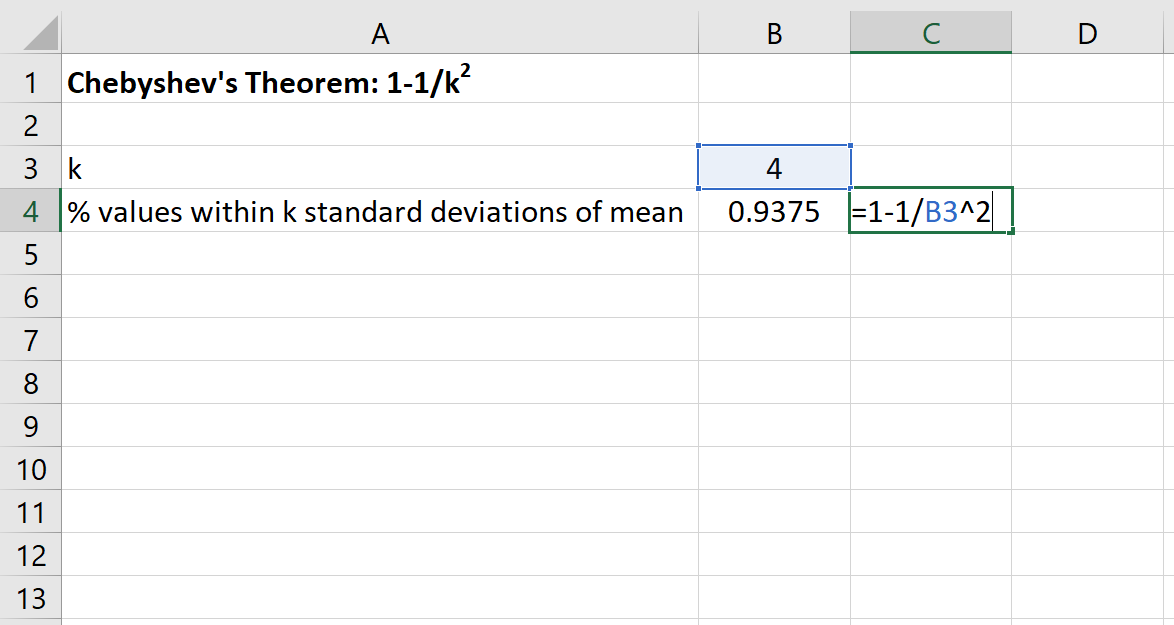
该数据集的 80 到 120 之间的值的百分比将至少为 93.75% 。