如何解读二项式分布表
二项式分布表 是一个显示与二项式分布相关的概率的表。要使用二项分布表,您只需要三个值:
- n:尝试次数
- r: n次尝试中“成功”的次数
- p:给定试验的成功概率
使用这三个数字,您可以使用二项式分布表来查找在n次试验中获得r次成功的概率(当每次试验的成功概率为p时)。
以下示例说明了如何读取二项式分布表。
实施例1
问题:杰西卡的罚球命中率为 60%。如果她罚球 6 次,那么她恰好罚中 4 球的概率是多少?
为了回答这个问题,我们可以在二项式分布表中找到对应于n = 6、 r = 4、 p = 0.60的值:
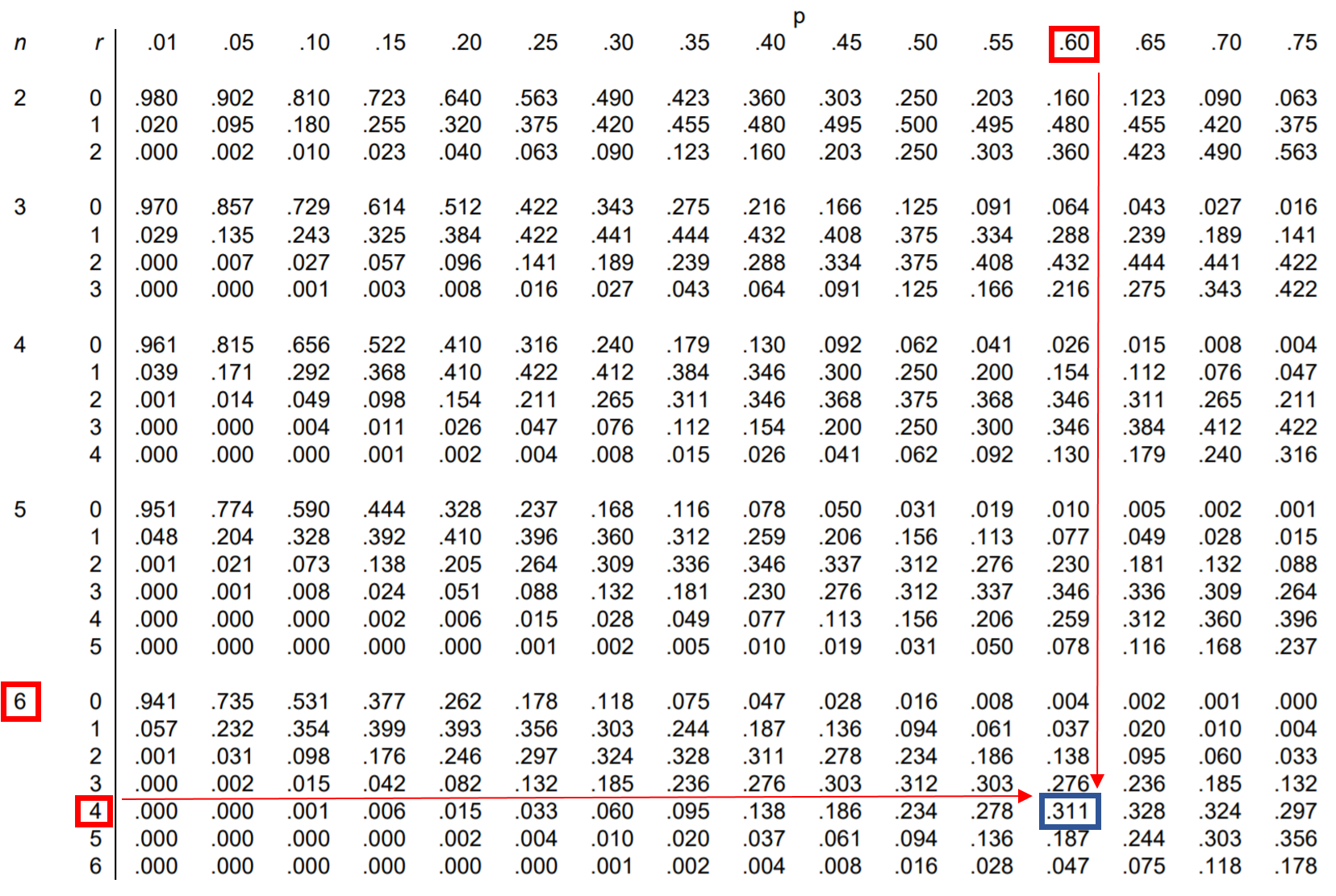
杰西卡 6 次罚球中准确命中 4 次的概率是0.311 。
实施例2
问题:杰西卡的罚球命中率为 60%。如果她罚球 6 次,那么她罚球少于 4 次的概率是多少?
要找到这个概率,您实际上必须添加以下概率:
P(小于 4) = P(制作 0) + P(制作 1) + P(制作 2) + P(制作 3)
因此,我们可以在二项式分布表中查找这四个概率中的每一个并将它们加在一起:
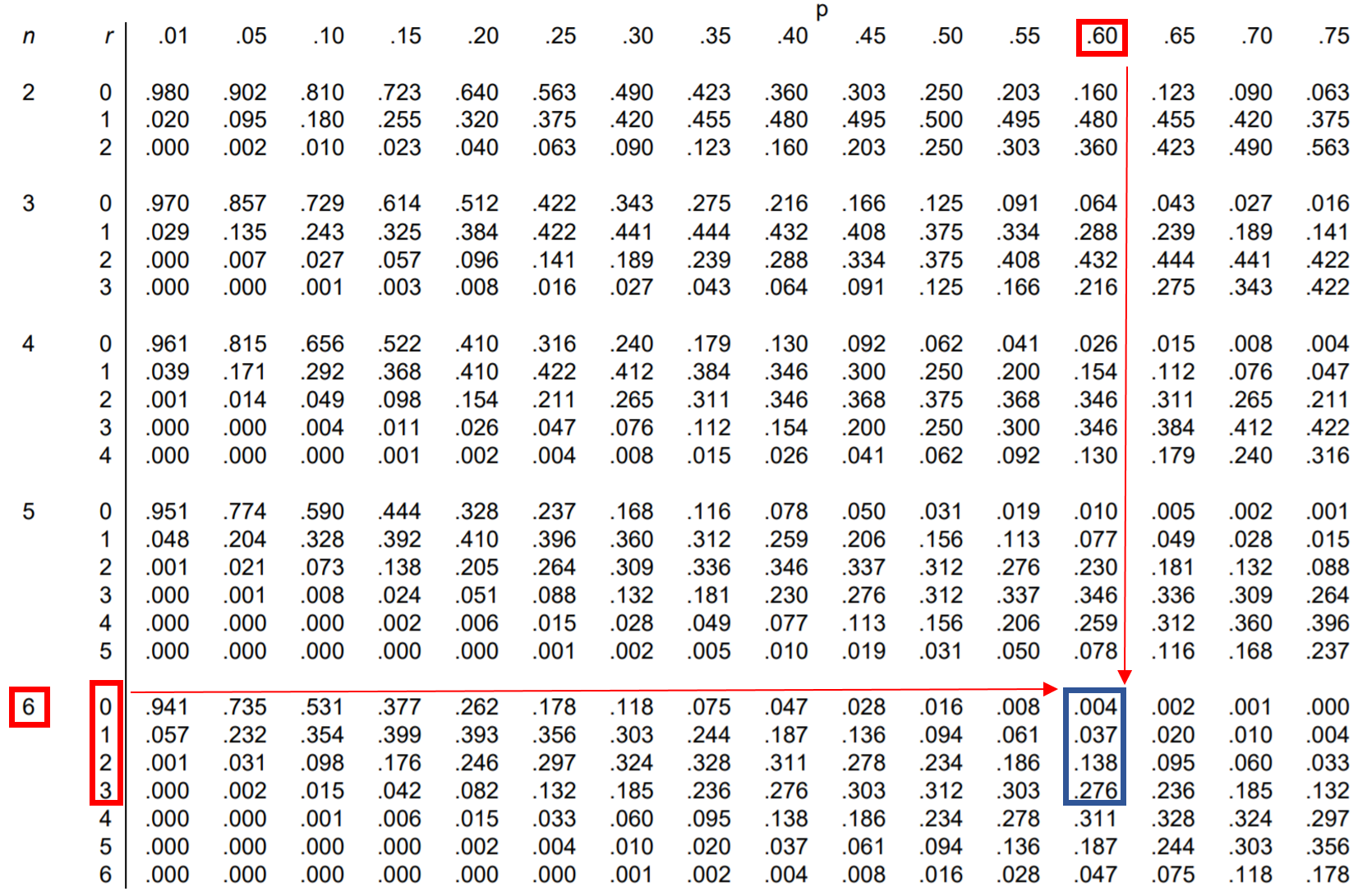
从表中可以看出,P(小于 4) = .004 + .037 + .138 + .276 = 0.455 。
杰西卡罚球少于 4 次的概率是0.455 。
实施例3
问题:杰西卡的罚球命中率为 60%。如果她罚球 6 次,那么她罚中 4 次或更多的概率是多少?
为了找到这个概率,我们必须添加以下概率:
P(制作 4 个或更多) = P(制作 4) + P(制作 5) + P(制作 6)
因此,我们可以在二项式分布表中查找这三个概率并将它们加在一起:
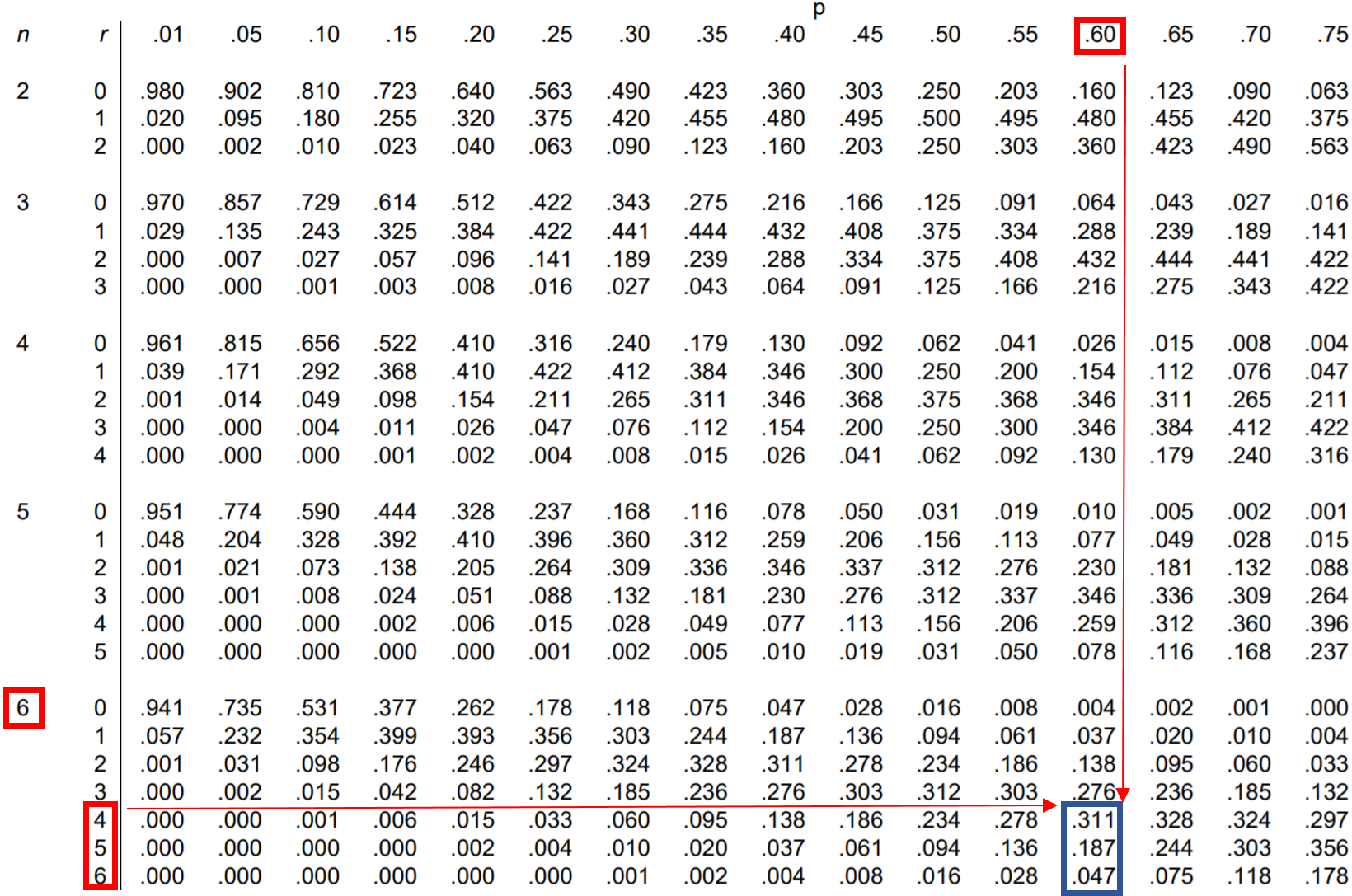
从表中可以看出,P(使 4 个或更多) = .311 + .187 + .047 = 0.545 。
杰西卡罚球 4 次或以上的概率为0.545 。