Fisher 精确检验:定义、公式和示例
Fisher 精确检验用于确定两个 calcategories 变量之间是否存在显着关联。当 2 × 2 表中的一个或多个单元格计数小于 5 时,它通常用作独立性卡方检验的替代方法。
Fisher 精确检验使用以下原假设和备择假设:
- H 0 :(零假设)两个变量是独立的。
- H 1 :(替代假设)两个变量不是独立的。
假设我们有以下 2×2 表:
| 第 1 组 | 第2组 | 总行数 | |
| 第 1 类 | 有 | 乙 | a+b |
| 第2类 | 与 | d | c+d |
| 总栏 | 一个+c | 乙+d | a+b+c+d = n |
Fisher 精确检验的单侧 p 值计算如下:
p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
这会产生与具有以下参数的超几何分布的 CDF 相同的 p 值:
- 人口规模 = n
- 人口的“成功”=a+b
- 样本量 = a + c
- “成功”的例子 = 1
Fisher 精确检验的两侧 p 值计算起来不太简单,并且不能通过简单地将一侧 p 值乘以 2 来找到。要查找双尾 p 值,我们建议使用Fisher 精确检验计算器。
Fisher 精确检验:示例
假设我们想知道性别是否与对政党的偏好相关。我们对 25 名选民进行了简单的随机抽样,并询问他们的政党偏好。下表列出了调查结果:
| 民主党人 | 共和党人 | 全部的 | |
| 男性 | 4 | 9 | 13 |
| 女性 | 8 | 4 | 12 |
| 全部的 | 12 | 13 | 25 |
步骤 1:定义假设。
我们将使用以下假设执行 Fisher 精确检验:
- H 0 :性别和政党偏好是独立的。
- H 1 :性别和政党偏好不是独立的。
步骤 2:计算双尾 p 值。
我们可以使用Fisher 精确检验计算器并输入以下内容:
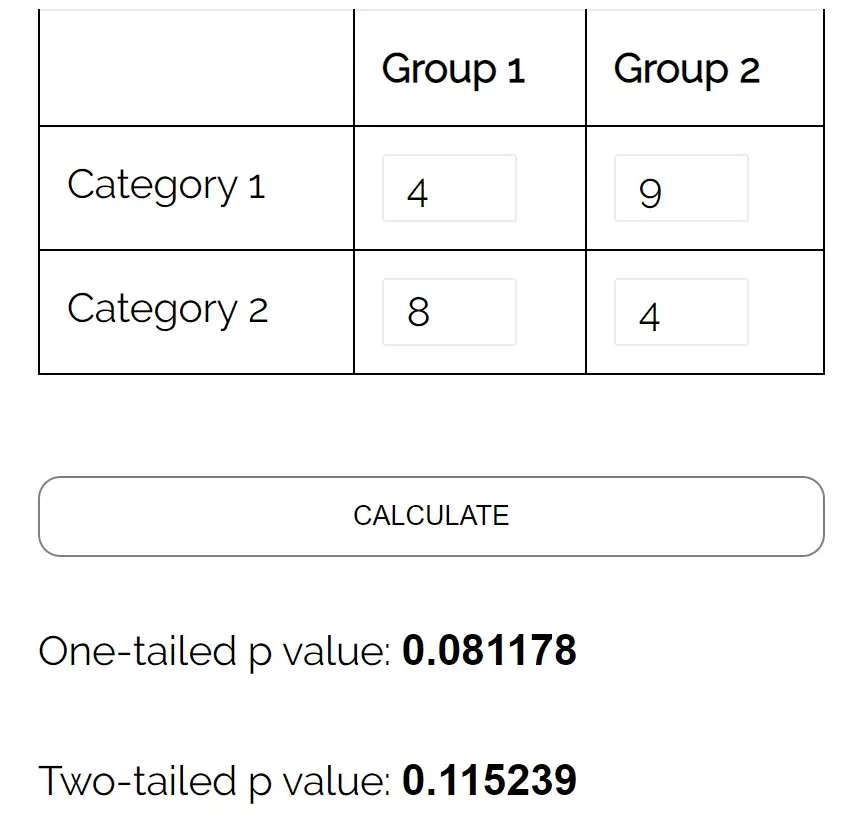
双尾 p 值为0.115239 。该值小于 0.05,我们无法拒绝原假设。我们没有足够的证据表明性别和对政党的偏好之间存在统计学上的显着关联。
其他资源
以下教程解释了如何使用不同的统计程序执行 Fisher 精确检验:
如何在 R 中执行 Fisher 精确检验
如何在 Excel 中执行 Fisher 精确检验
如何在 Stata 中进行 Fisher 精确检验
如何在 SPSS 中执行 Fisher 精确检验
如何在 Python 中执行 Fisher 精确检验
费舍尔精确检验计算器