协方差
本文解释了什么是协方差以及它是如何计算的。您将找到协方差公式以及计算数据集协方差的示例。此外,您还可以使用最后的在线计算器计算任何数据系列的协方差。
什么是协方差?
在统计学中,协方差是表示两个随机变量联合变异程度的值。换句话说,协方差用于分析两个变量之间的相关性。
协方差等于两个变量的数据与其各自均值之差的乘积之和除以数据总数。

👉您可以使用下面的计算器来计算任何数据集的协方差。
协方差值的解释非常简单:
- 如果协方差为正,则表示两个变量之间存在相关性。因此,当一个变量的值增加时,另一个变量也会增加,反之亦然。
- 如果协方差为负,则表示两个变量之间的关系为负。因此,当一个变量的值增加时,另一个变量的值就会减少,反之亦然。
- 如果协方差为零(或其值接近零),则意味着两个变量之间不存在关系。换句话说,两个随机变量是独立的。
如何计算协方差
要计算数据系列的协方差,必须执行以下步骤:
- 分别计算每个变量的平均值。
- 对于每个变量,求其每个值与该变量均值之间的差。
- 将每个数据点在上一步中计算出的差异相乘。
- 将上一步获得的所有结果相加。
- 除以数据总数。获得的值是数据序列的协方差。
综上所述,计算两个变量之间协方差的公式如下:
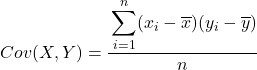
强烈推荐的提取两个变量之间协方差的方法是创建一个包含所有数据对的表,并为上述每个步骤添加一列。这样你的计算就会变得更好,你也会更好地理解你在做什么。
协方差计算示例
考虑到协方差的定义,下面是计算此类统计度量的分步示例。目的是让您更好地理解协方差的概念以及如何分析两个变量之间的相关性。
- 计算以下统计数据集的协方差:

首先,我们需要计算每个变量的算术平均值。为此,我们将每个变量值的总和除以数据总数。
![]()
![]()
一旦我们确定了每个随机变量的均值,我们就可以将以下列添加到数据表中以获得协方差:
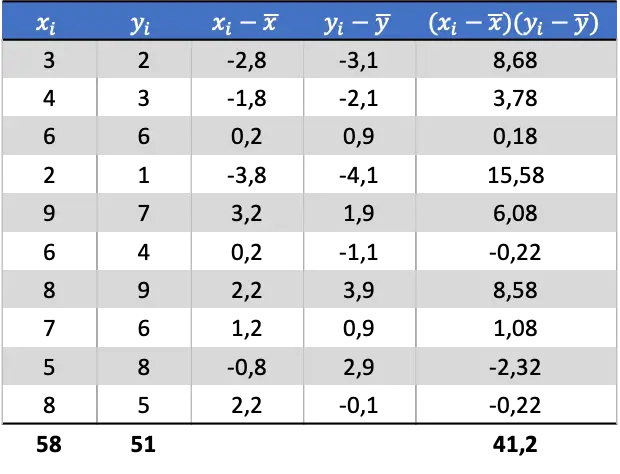
因此,要确定两个变量的协方差,您必须将最后一列的总和除以数据对的数量:
![Rendered by QuickLaTeX.com \begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-49b4992f8443e4d94e38dfa56da38a9a_l3.png)
在这种情况下,协方差值为正,这意味着所研究的两个随机变量之间存在直接依赖性。然而,如果协方差值为负,则意味着两个变量之间的相关性是相反的。最后,如果协方差值为零或非常接近零,则意味着两个变量之间不存在线性关系。
从求解此示例中可以看出,使用 Excel 等计算机程序将列添加到表中并快速执行计算非常有用。否则,通过手动计算运算,找到协方差需要更长的时间。
协方差计算器
在下面的计算器中输入一组统计数据来计算两个变量之间的协方差。您需要分隔数据对,以便第一个框中只有一个变量的值,第二个框中只有第二个变量的值。
数据必须用空格分隔,并使用句点作为小数点分隔符输入。
协方差属性
协方差具有以下性质:
- 随机变量和常数之间的协方差为零。
![]()
- 变量与其自身的协方差等于该变量的方差。
![]()
- 协方差满足对称性,因此变量X和Y的协方差等于变量Y和X的协方差。变量的顺序不影响协方差的结果。
![]()
- 如果变量乘以常数,可以先计算协方差,然后将结果乘以常数。
![]()
- 向变量添加项不会影响协方差结果。
![]()
- 两个随机变量之间的协方差与其数学期望有关。变量X和Y之间的协方差等于X和Y乘积的数学期望减去每个变量的数学期望的乘积。
![]()
- 当使用变量进行操作时,下面的代数表达式是关于协方差的:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5d429b5bb4e4796cc5b8c73ed0845fa2_l3.png)