如何在 spss 中进行逻辑回归
逻辑回归是当响应变量是二元时我们用来拟合回归模型的方法。
本教程介绍如何在 SPSS 中执行逻辑回归。
示例:SPSS 中的逻辑回归
使用以下步骤在 SPSS 中对数据集执行逻辑回归,该数据集指示大学篮球运动员是否根据 GPA 被选入 NBA(选秀:0 = 否,1 = 是)。每场比赛的得分和他们的分区级别。
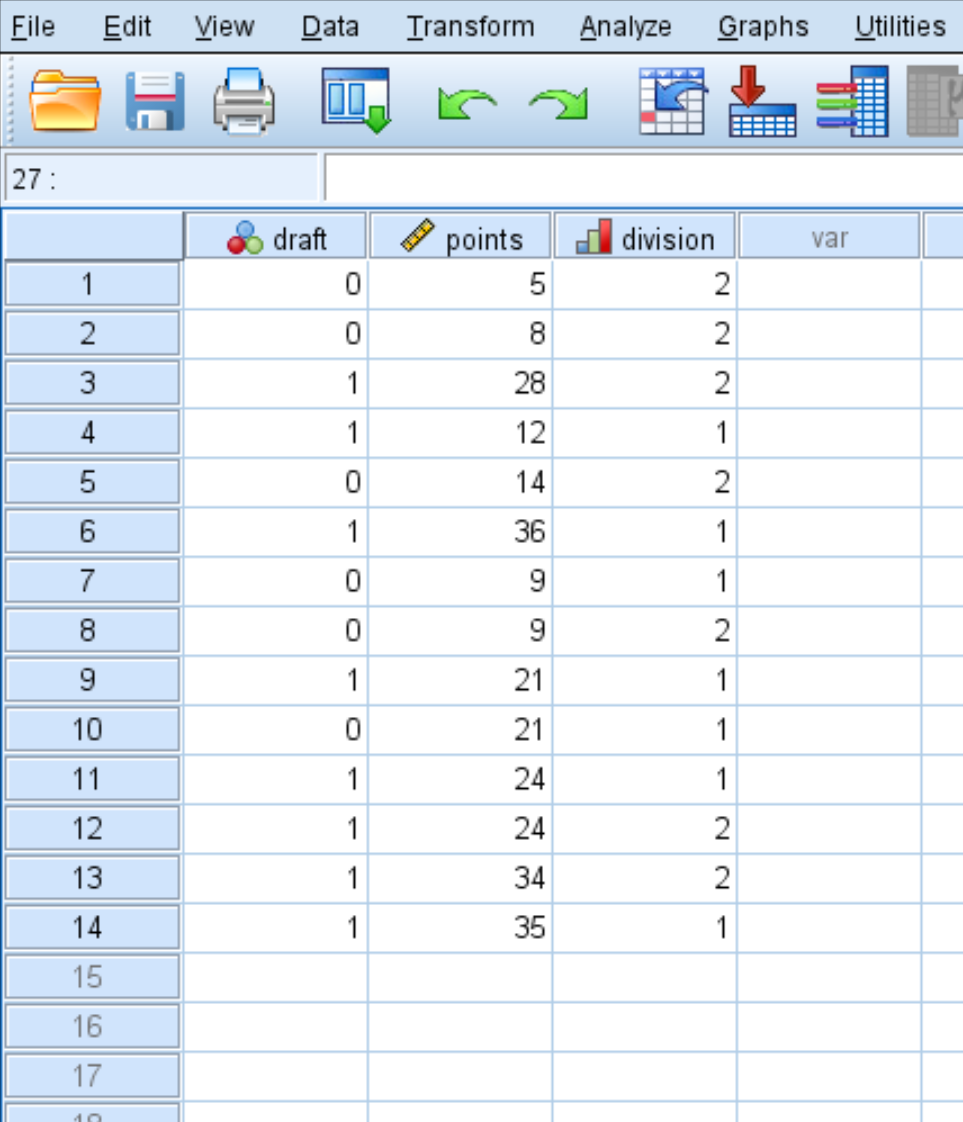
第 1 步:输入数据。
首先,输入以下数据:
步骤 2:执行逻辑回归。
单击“分析”选项卡,然后单击“回归” ,然后单击“二元 Logistic 回归” :
在出现的新窗口中,将二元响应变量项目拖到标记为“Dependent”的区域中。然后将预测变量的冒号和除号拖到标记为 Block 1 of 1 的框中。将方法设置保留为 Enter。然后单击“确定” 。
步骤 3. 解释结果。
单击“确定”后,将出现逻辑回归结果:
以下是如何解释结果:
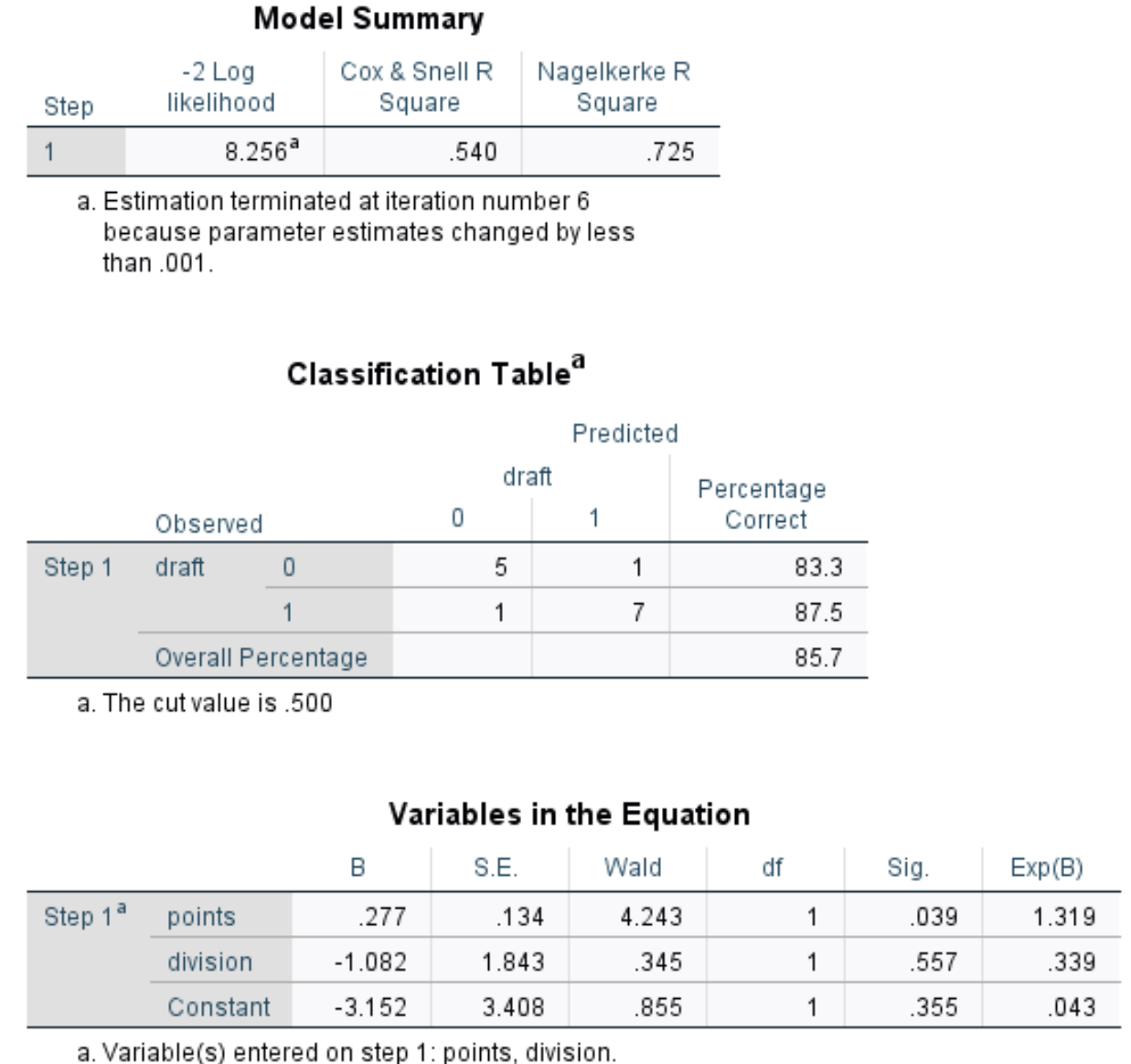
模型摘要:此表中最有用的指标是 Nagelkerke R Square,它告诉我们可以由预测变量解释的响应变量的变化百分比。在这种情况下,分数和划分可以解释72.5%的选秀变异性。
分类表:此表中最有用的指标是总体百分比,它告诉我们模型能够正确分类的观测值的百分比。在这种情况下,逻辑回归模型能够正确预测85.7%球员的选秀结果。
方程中的变量:最后一个表为我们提供了一些有用的测量结果,包括:
- Wald:每个预测变量的Wald检验统计量,用于确定每个预测变量是否具有统计显着性。
- Sig:对应于每个预测变量的 Wald 检验统计量的 p 值。我们看到点的 p 值为 0.039,除法的 p 值为 0.557。
- Exp(B):每个预测变量的优势比。这告诉我们与给定预测变量增加一个单位相关的球员被选秀几率的变化。例如,2级球员被选中的几率仅为1级球员被选中的几率的0.339。同样,每场比赛得分每增加一个单位,球员被选中的几率就会增加 1,319 倍。
然后,我们可以使用系数(标记为 B 的列中的值)来预测给定球员被选中的概率,使用以下公式:
概率 = e -3.152 + 0.277(点)– 1.082(除法) /(1+e -3.152 + 0.277(点)– 1.082(除法) )
例如,一名场均得分为 20 分并且在第 1 组比赛的球员被选中的概率可以计算如下:
概率 = e -3.152 + 0.277(20) – 1.082(1) / (1+e -3.152 + 0.277(20) – 1.082(1) ) = 0.787 。
由于该概率大于 0.5,因此我们预测该球员将被选中。
步骤 4. 报告结果。
最后,我们想报告逻辑回归的结果。以下是如何执行此操作的示例:
进行逻辑回归以确定每场比赛的得分和分区级别如何影响篮球运动员被选中的概率。分析中总共使用了 14 名球员。
该模型解释了项目结果中 72.5% 的差异,并正确分类了 85.7% 的案例。
2级球员被选中的几率仅为1级球员被选中的几率的0.339。
每场比赛得分每增加一个单位,球员被选中的几率就会增加 1,319 倍。