如何在 spss 中计算 z 分数
z 分数告诉我们给定值与平均值的标准差有多少。
给定值的 z 分数计算如下：
z 分数= (x – μ) / σ
金子：
- x：个体值
- μ：总体平均值
- σ：总体标准差
本教程介绍如何在 SPSS 中计算 z 分数。
相关：如何解释 Z 分数
如何在 SPSS 中计算 Z 分数
假设我们有以下数据集，显示 15 人的年收入（以千为单位）：
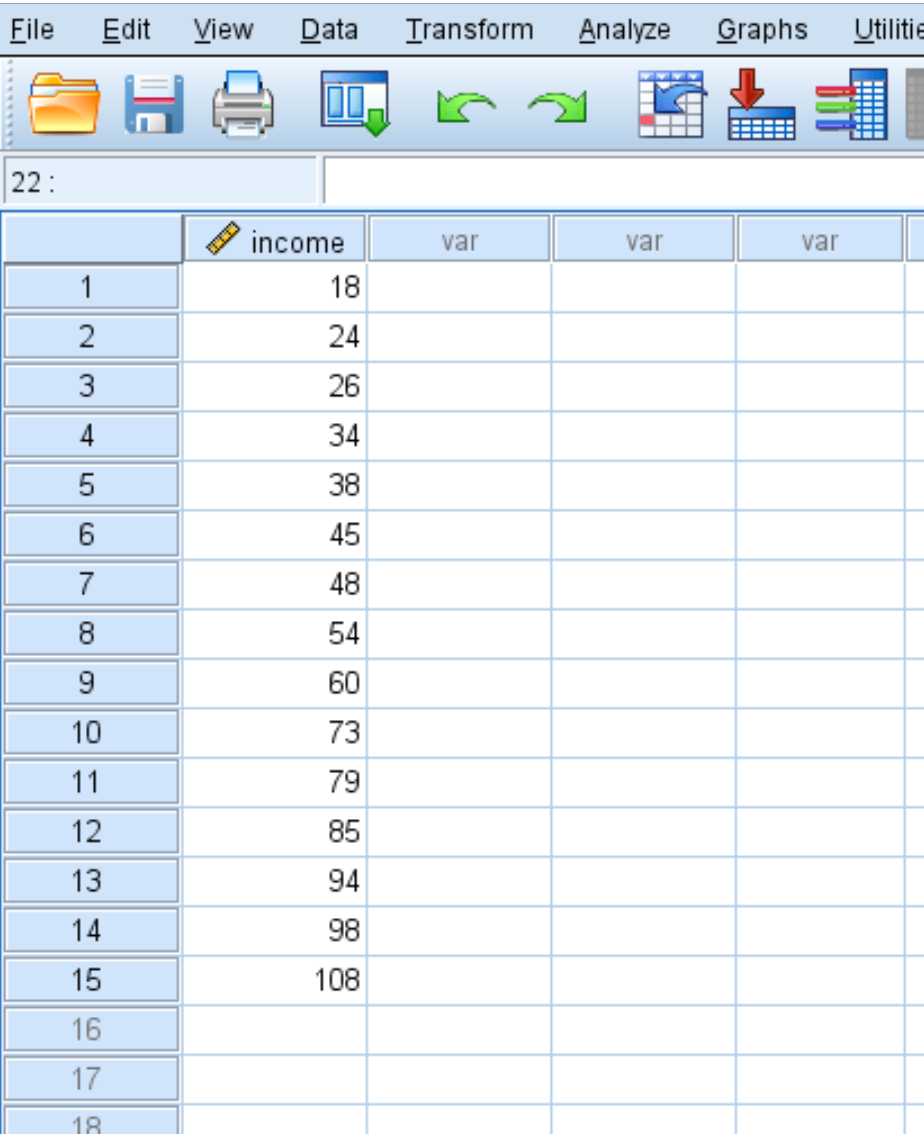
要计算数据集中每个值的 z 分数，请依次单击“分析”选项卡、 “描述性统计”和“描述性” ：
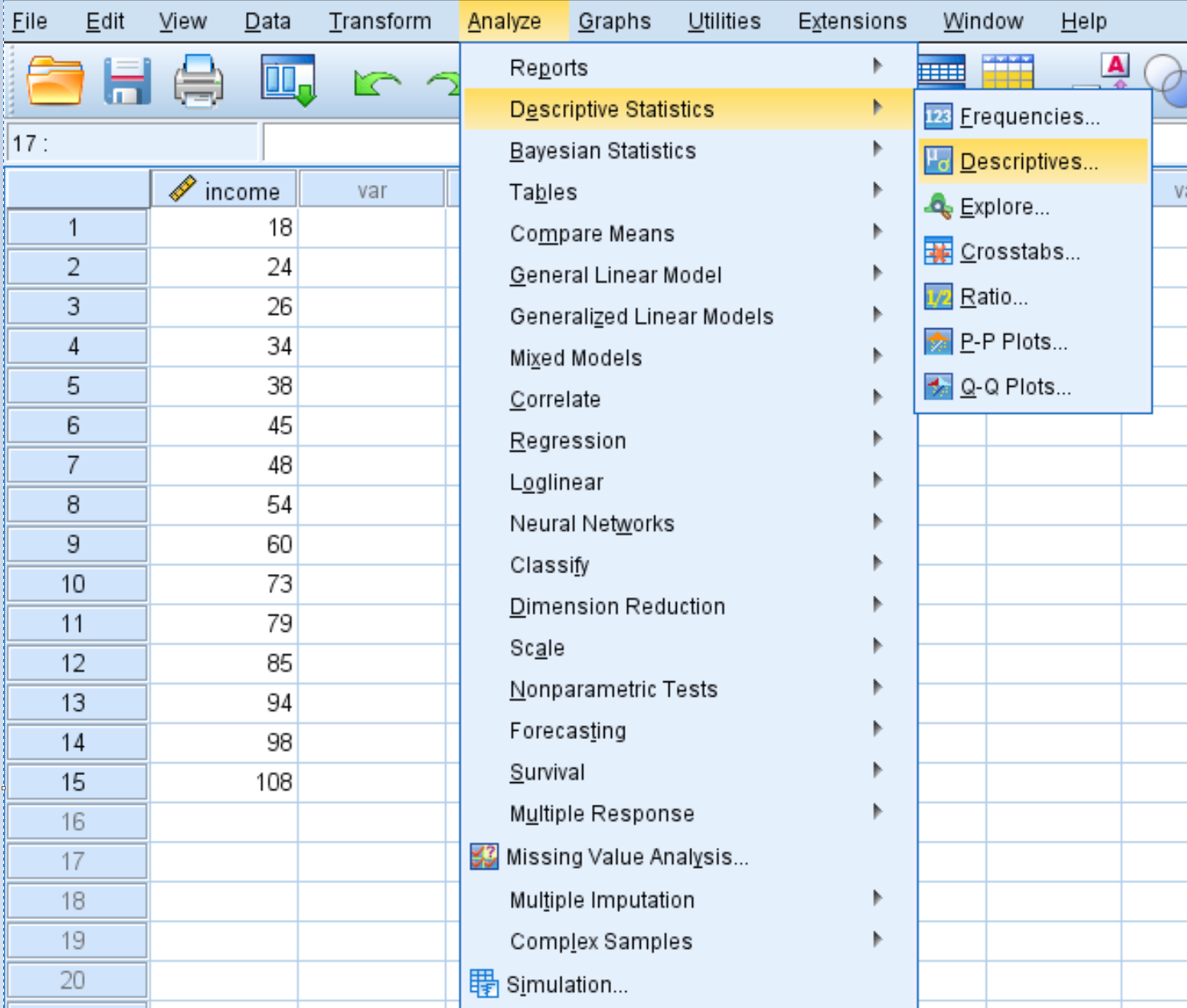
在出现的新窗口中，将收入变量拖到标记为“变量”的框中。
确保选中“将标准化值另存为变量”旁边的框，然后单击“确定” 。
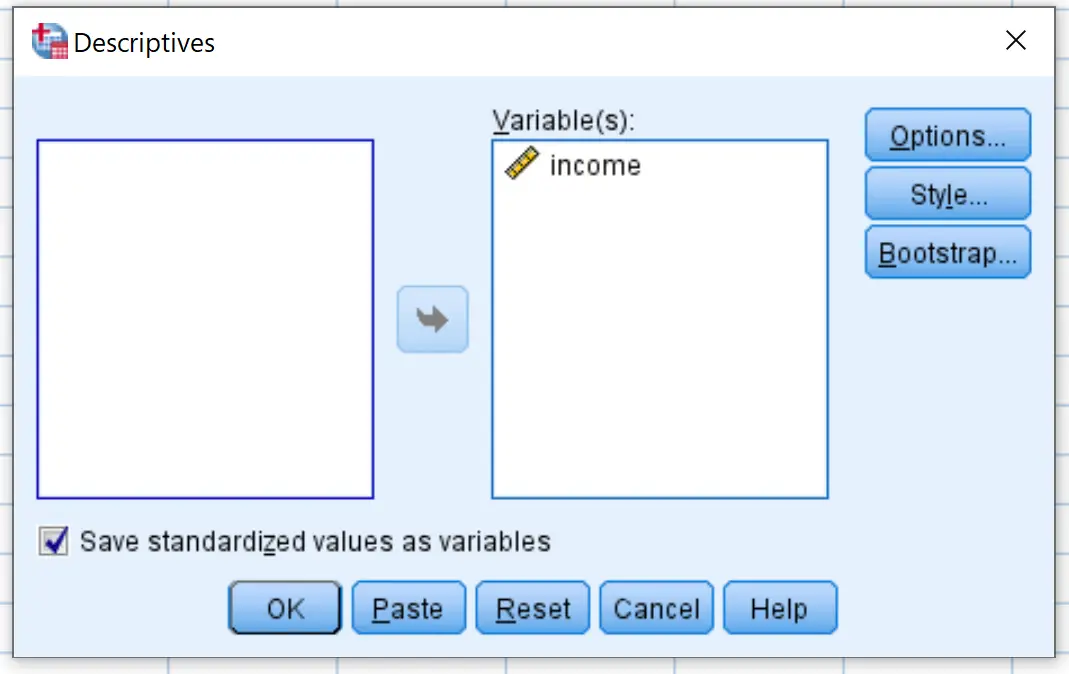
单击“确定”后，SPSS 将为您的数据集生成一个描述性统计表：
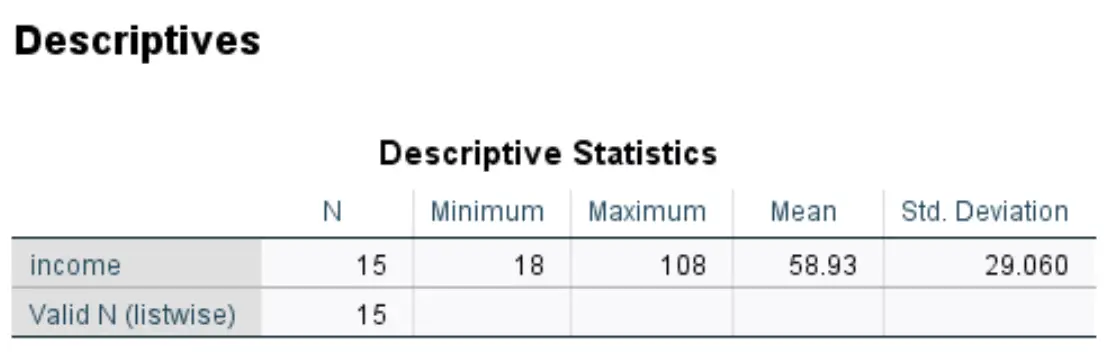
SPSS 还将生成一个新的值列，显示数据集中每个原始值的 z 分数：
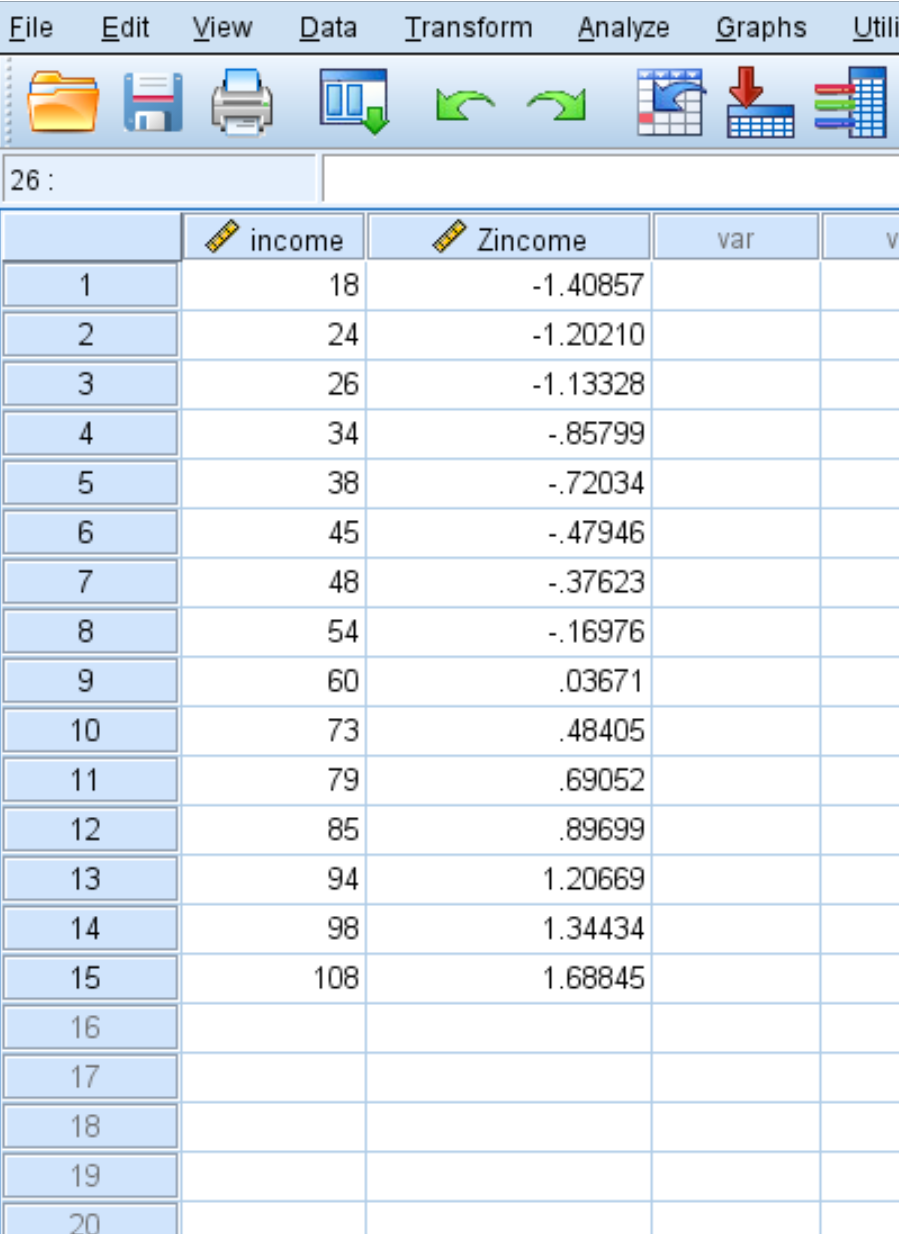
每个 z 分数均使用公式 z = (x – μ) / σ 计算
例如，收入值 18 的 z 分数为：
z = (18 – 58.93) / 29.060 = -1.40857 。
所有其他数据值的 Z 分数均以相同的方式计算。
如何解释 Z 分数
请记住，z 分数只是告诉我们某个值与平均值的标准差有多少。
z 分数可以是正数、负数或等于 0：
- 正 z 分数表示特定值高于平均水平。
- 负 z 分数表示特定值低于平均水平。
- z 分数为零表示特定值等于平均值。
在我们的示例中，我们发现平均值为 58.93，标准差为 29.060。
因此，我们数据集中的第一个值是 18，其 z 分数为 (18 – 58.93) / 29.060 = -1.40857 。
这意味着值“18”比平均值低1.40857 个标准差。
相反，我们数据中的最后一个值为 108，对应的 z 分数为 (108 – 58.93) / 29.060 = 1.68845 。
这意味着值“108”比平均值高1.68845 个标准差。
其他资源
以下教程说明如何在 SPSS 中执行其他常见任务：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多