Binompdf 与 binomcdf：区别（以及示例）

二项分布是所有统计中最常用的分布之一。

在 TI-84 计算器上，您可以使用两个函数来查找与二项式分布相关的概率：

• binompdf(n, p, x) ：查找在n次试验过程中恰好发生x 次成功的概率，其中给定试验的成功概率等于p 。
• binomcdf(n, p, x) ：查找在n次试验中发生x或更少成功的概率，其中给定试验的成功概率等于p 。

您可以通过按2nd然后按VARS来访问 TI-84 计算器上的每个功能。这将带您进入DISTR屏幕，您可以在其中使用binompdf()和binomcdf() ：

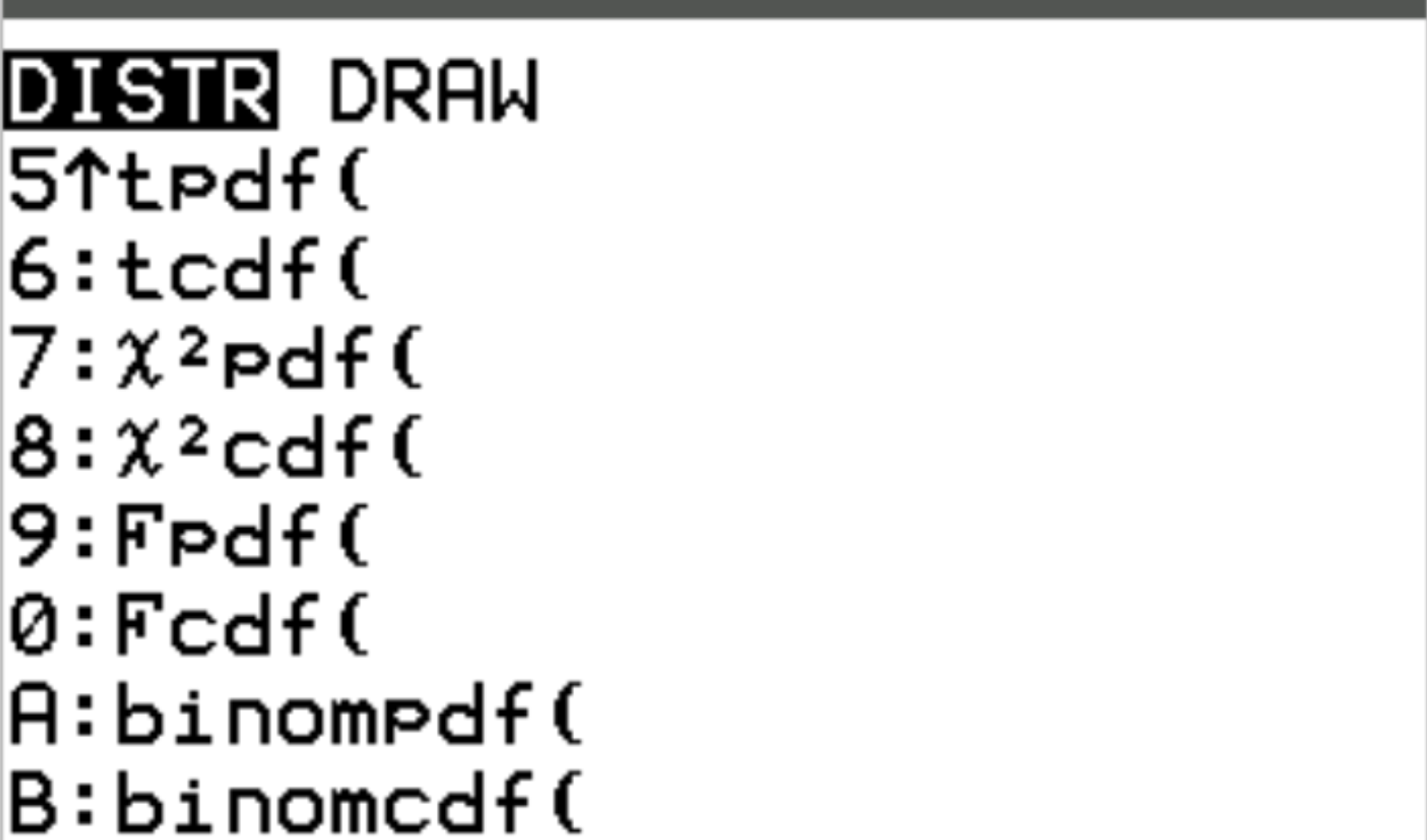
以下示例展示了如何在实践中使用每个函数。

示例：如何使用 Binompdf()

以下示例显示如何使用binompdf()函数。

示例 1：罚球尝试

杰西卡的罚球命中率为 80%。如果她罚球 10 次，那么她恰好罚中 7 球的概率是多少？

为了回答这个问题，我们可以输入以下公式：

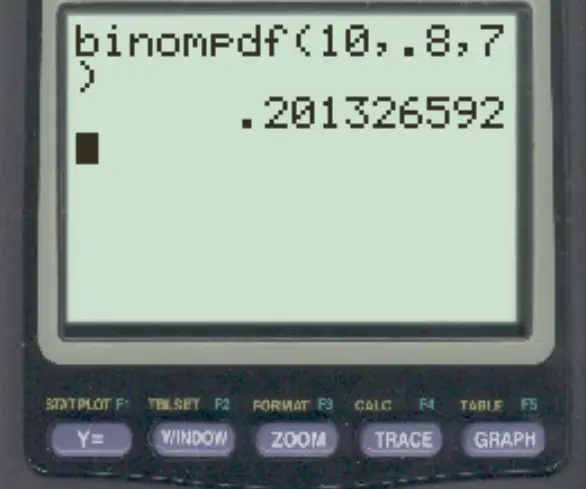
她恰好得到 7 的概率是0.2013 。

示例2：欺诈交易

银行知道所有交易中有 3% 是欺诈性的。如果某一天发生 20 笔交易，那么恰好有 2 笔交易是欺诈的概率是多少？

为了回答这个问题，我们可以输入以下公式：

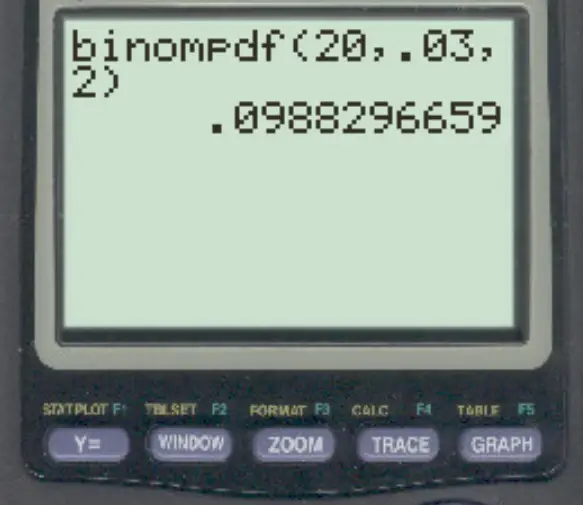
正好有 2 笔交易是欺诈的概率是0.0988 。

示例：如何使用 Binomcdf()

以下示例显示如何使用binomcdf()函数。

示例 1：罚球尝试

杰西卡的罚球命中率为 50%。如果她罚球 10 次，那么她罚球 7 次或更少的概率是多少？

为了回答这个问题，我们可以输入以下公式：

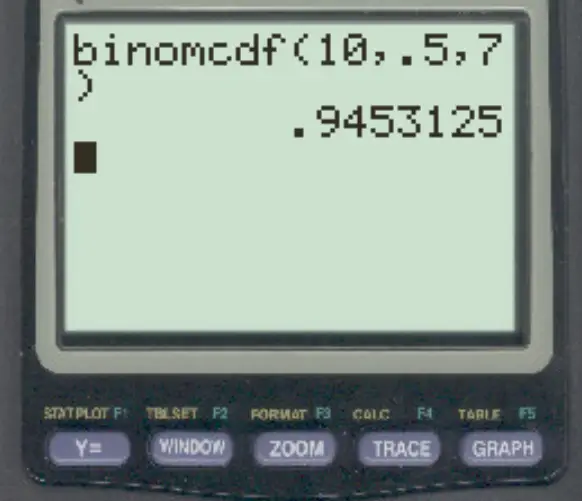
她罚球 7 次或更少的概率是0.9453 。

示例2：欺诈交易

银行知道所有交易中有 3% 是欺诈性的。如果某一天发生 20 笔交易，那么超过 2 笔交易是欺诈的概率是多少？

为了回答这个问题，我们可以输入以下公式：

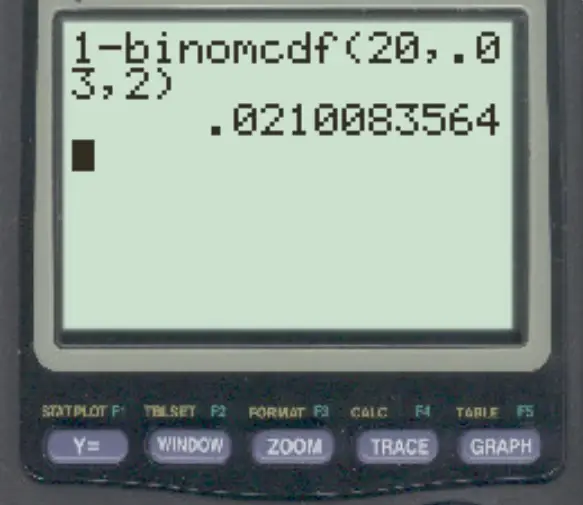
超过 2 笔交易属于欺诈的概率为0.021 。

其他资源

二项式分布计算器
如何在 Excel 中执行二项式检验