如何在 excel 中执行 bonferroni 校正

Bonferroni 校正是指调整一系列统计检验的 alpha (α) 水平以控制出现 I 类错误的概率的过程。

Bonferroni 校正的公式如下：

α_新= α_原始/ n

金子：

• _原始α：原始α水平
• n：执行的比较或测试的总数

例如，如果我们同时运行三个统计测试并希望每次测试都使用 α = 0.05，则 Bonferroni 校正告诉我们应该使用 α _new = 0.01667 。

_新α =_原始α / n = 0.05 / 3 = 0.01667

因此，如果检验的 p 值小于 0.01667，我们只应拒绝每个单独检验的原假设。

当我们希望同时比较多个组均值时，通常在方差分析后的事后检验中进行这种类型的校正。

以下分步示例演示了如何在 Excel 中进行单向方差分析后执行 Bonferroni 校正。

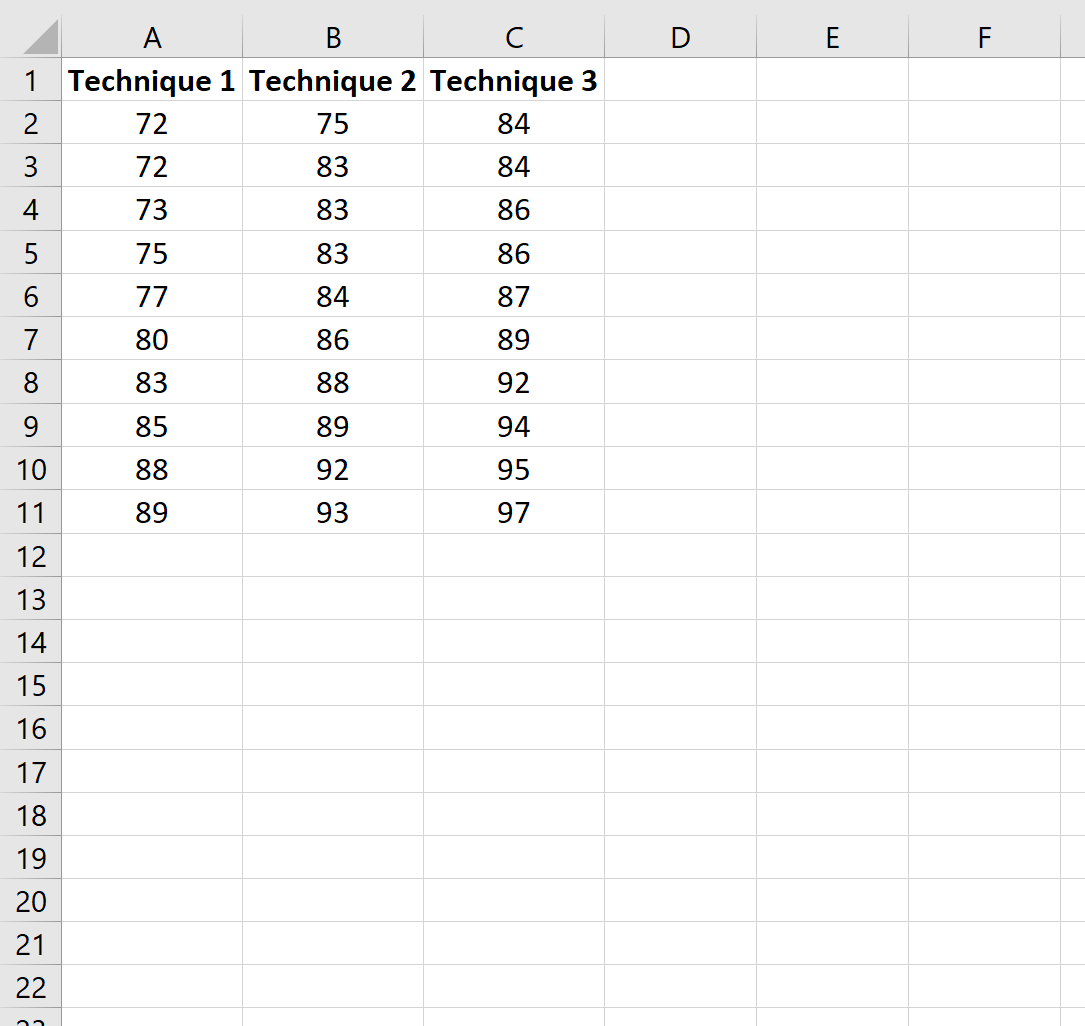
第 1 步：创建数据

首先，让我们创建一个假数据集，显示使用三种不同学习技巧之一来准备考试的学生的结果：

第 2 步：执行单向方差分析

接下来，让我们执行单向方差分析来确定三组的平均考试成绩是否相等。

首先，突出显示所有数据，包括列标题：

接下来，单击顶部功能区的“数据”选项卡，然后单击“数据分析” ：

如果此选项不可用，您必须首先加载分析工具库。

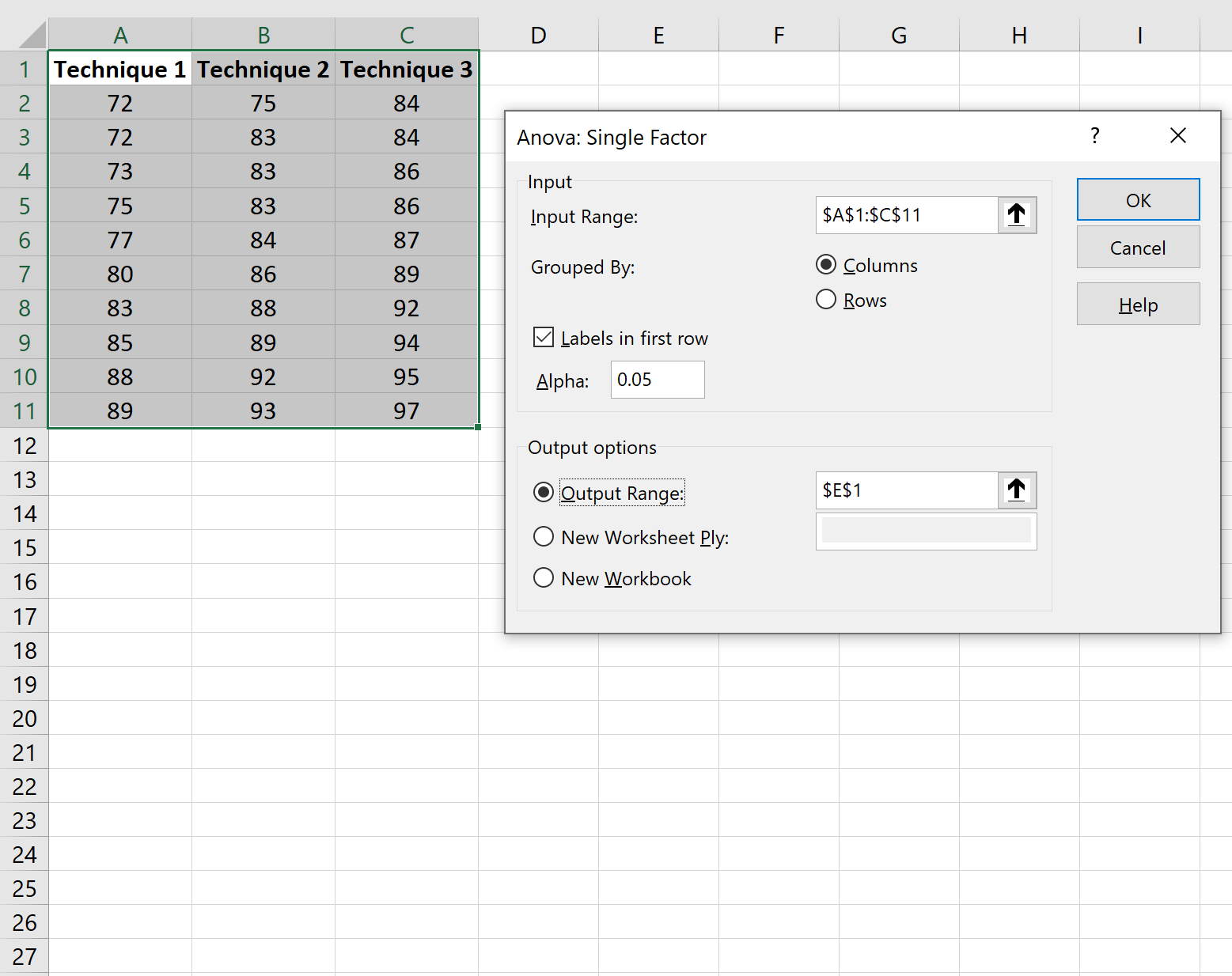
在出现的窗口中，单击方差分析：单因素，然后单击确定。

填写以下信息，然后单击“确定” ：

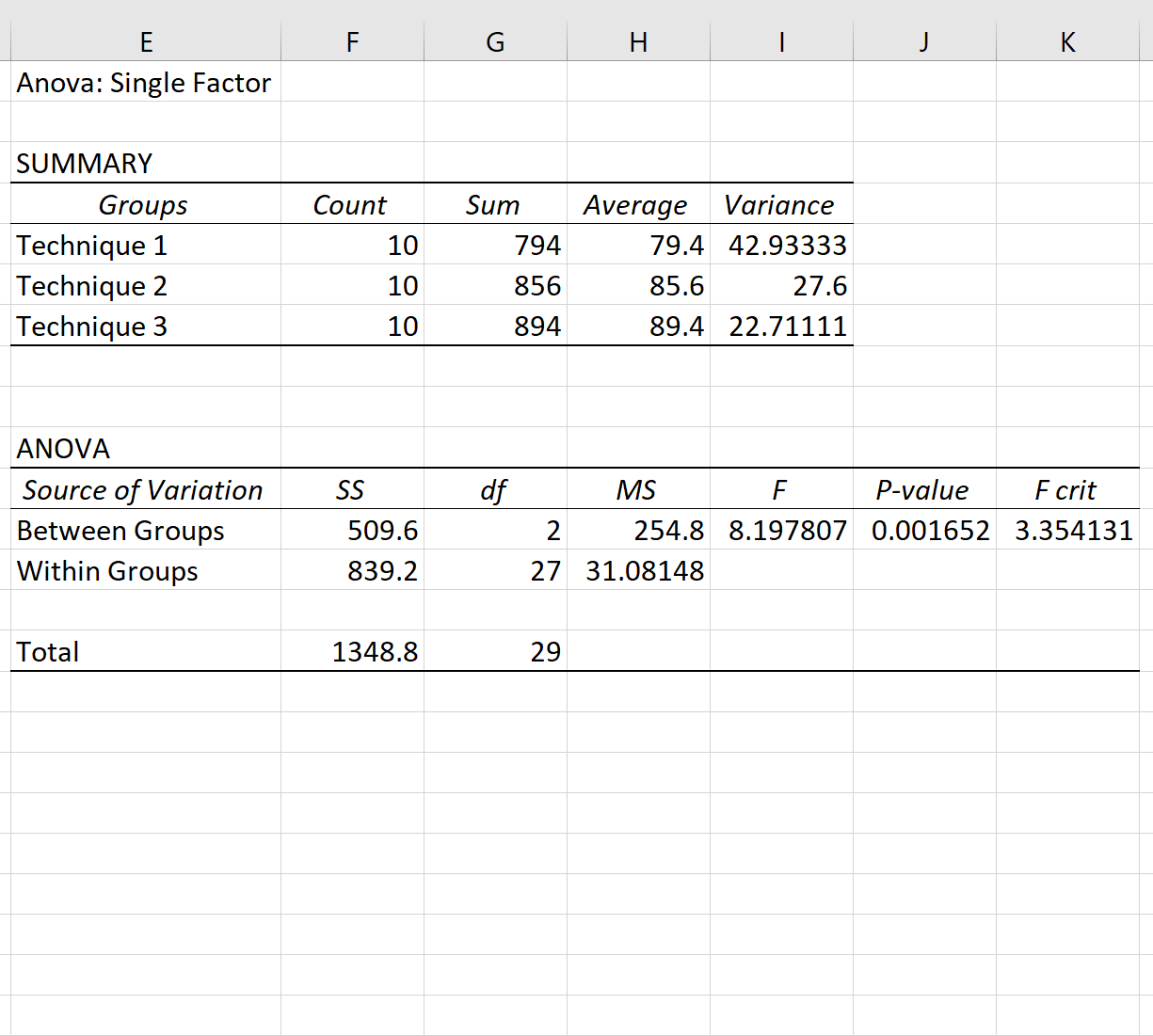
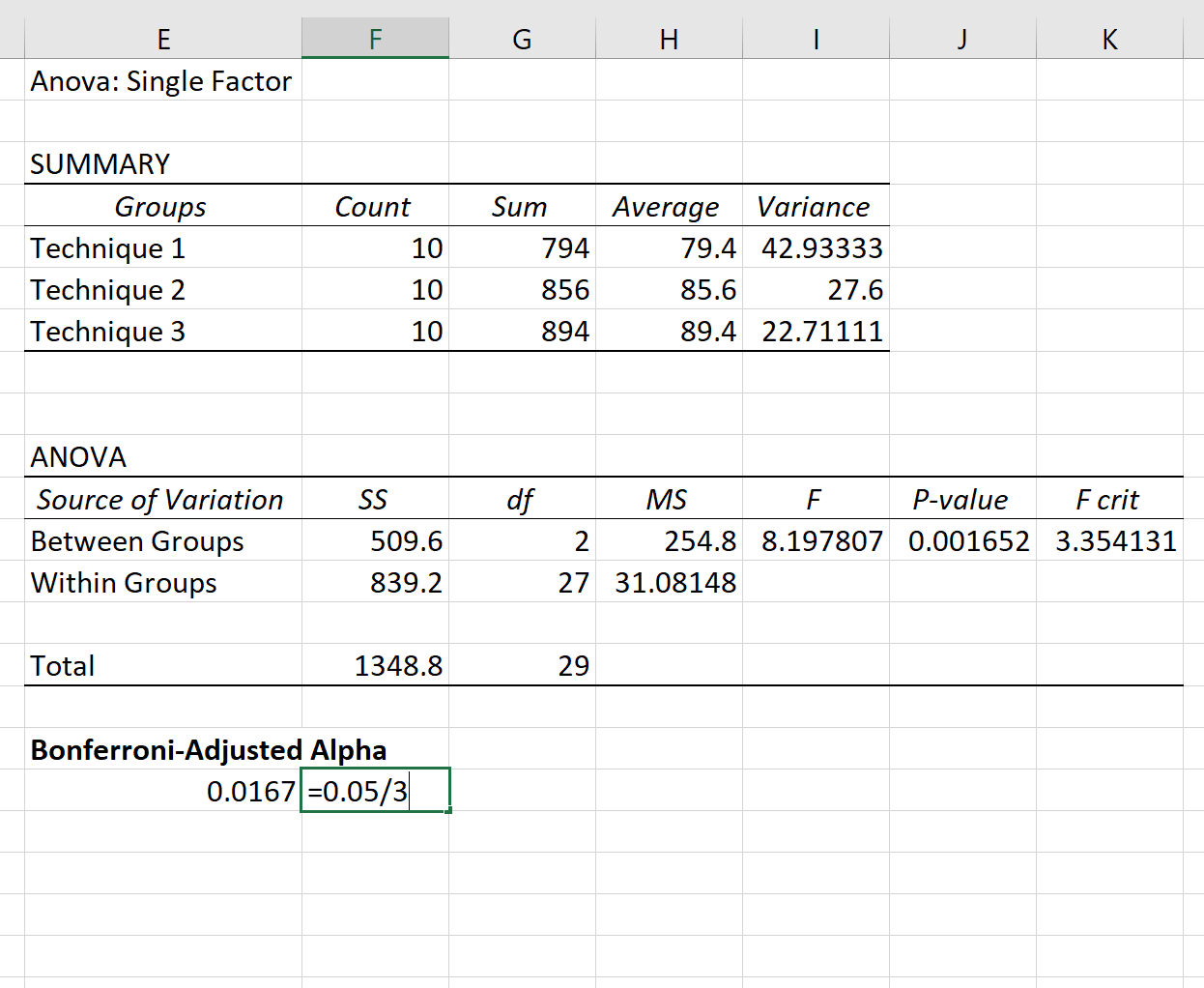
单向方差分析结果将自动出现：

回想一下，单向方差分析具有以下原假设和备择假设：

• H ₀ （零假设）：所有组均值相等。
• H _A （替代假设）：至少有一组平均值不同 休息。

由于方差分析表中的 p 值 (0.001652) 小于 0.05，因此我们有足够的证据来拒绝原假设。换句话说，三组之间的平均考试成绩并不相等。

然后我们可以使用三组之间的 Bonferroni 校正进行多次比较，以准确查看哪组均值不同。

步骤 3：使用 Bonferroni 校正执行多重比较

使用 Bonferroni 校正，我们可以计算调整后的 alpha 水平，如下所示：

α_新= α_原始/ n

在我们的示例中，我们将执行以下三个比较：

• 技术 1 与技术 2
• 技术 1 与技术 3
• 技术 2 与技术 3

由于我们希望对每个测试使用 α = .05 ，因此 Bonferroni 校正告诉我们应该使用 α _new = .0167 。

接下来，我们将使用 t 检验来比较每组之间的平均值。在 Excel 中，您可以使用以下语法：

=TTEST(表1、表2、队列=2、类型=2)

金子：

• Array1：第一个数据数组
• Array2：第二个数据数组
• tails：测试中的尾部数量。我们将使用“2”来表示双尾检验。
• type：要执行的 t 检验的类型。我们将使用“2”表示具有相等方差的 t 检验。

以下屏幕截图显示了如何执行每个 t 检验：

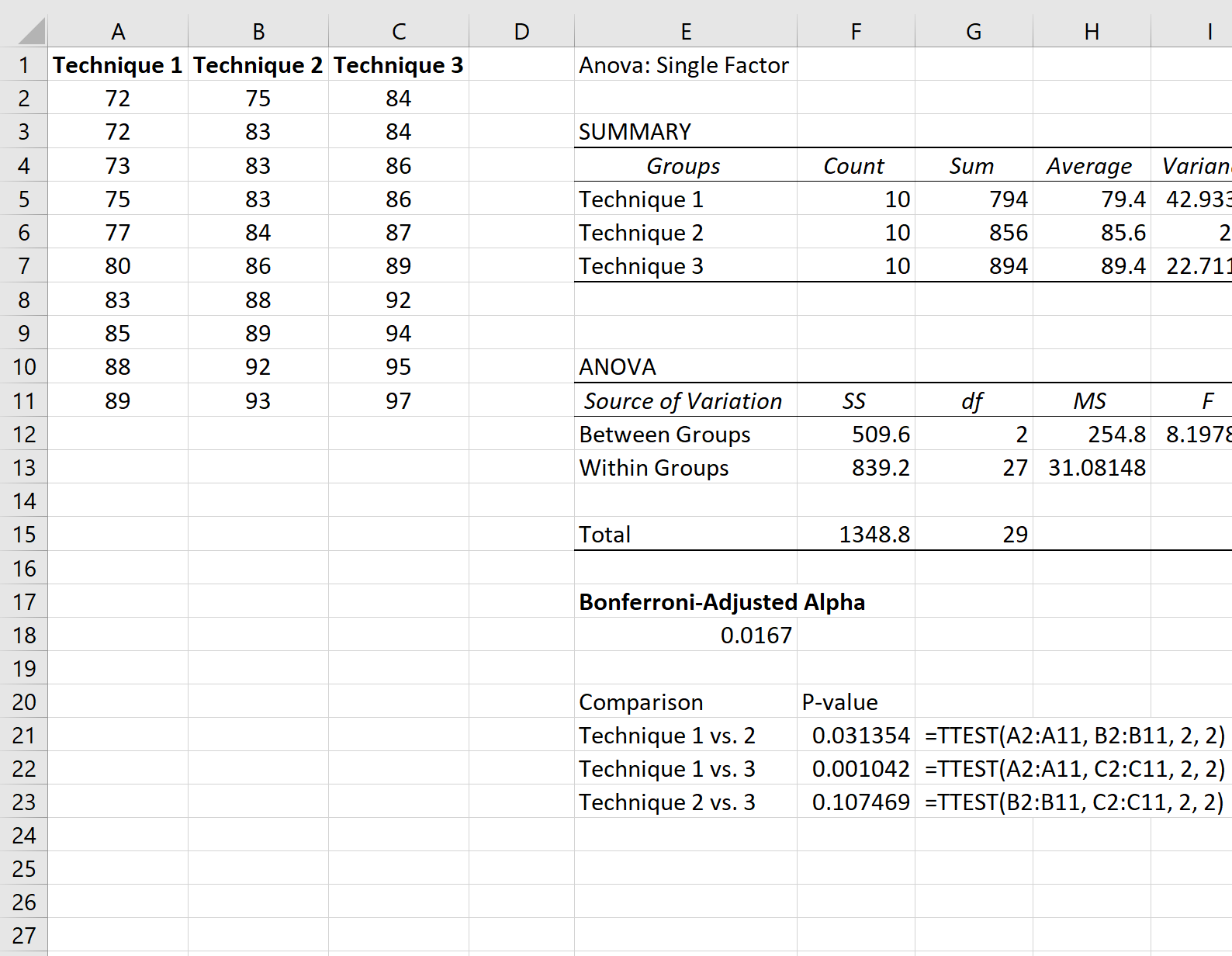
唯一低于 Bonferroni 调整 alpha 水平的 p 值来自技术 1 和技术 2 之间的比较，其 p 值为0.001042 。

因此，我们可以得出结论，技术 1 和技术 2 之间只有平均考试成绩存在统计学上的显着差异。

其他资源

每个家庭的错误率是多少？
Bonferroni 校正：定义和示例
Bonferroni 校正计算器