如何在 r 中执行 box-cox 变换(附示例)
Box-Cox 变换是将非正态分布的数据集变换为更正态分布的数据集的常用方法。
此方法背后的基本思想是使用以下公式找到 λ 值,使变换后的数据尽可能接近正态分布:
- y(λ) = (y λ – 1) / λ 如果 y ≠ 0
- y(λ) = log(y) 如果 y = 0
我们可以使用MASS()库中的boxcox()函数在 R 中执行 box-cox 转换。下面的例子展示了如何在实际中使用这个功能。
请参阅康涅狄格大学的这篇文章,了解 Box-Cox 变换发展的精彩总结。
示例:R 中的 Box-Cox 变换
以下代码演示如何将线性回归模型拟合到数据集,然后使用boxcox()函数查找最佳 lambda 来转换响应变量并拟合新模型。
library (MASS) #create data y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8) x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8) #fit linear regression model model <- lm(y~x) #find optimal lambda for Box-Cox transformation bc <- boxcox(y ~ x) (lambda <- bc$x[which.max(bc$y)]) [1] -0.4242424 #fit new linear regression model using the Box-Cox transformation new_model <- lm(((y^lambda-1)/lambda) ~ x)
最佳 lambda 为-0.4242424 。因此,新的回归模型将原始响应变量 y 替换为变量 y = (y -0.4242424 – 1) / -0.4242424。
以下代码展示了如何在 R 中创建两个QQ 图来可视化两个回归模型之间残差的差异:
#define plotting area op <- par(pty = "s", mfrow = c(1, 2)) #QQ plot for original model qqnorm(model$residuals) qqline(model$residuals) #QQ plot for Box-Cox transformed model qqnorm(new_model$residuals) qqline(new_model$residuals) #display both QQ plots by(op)
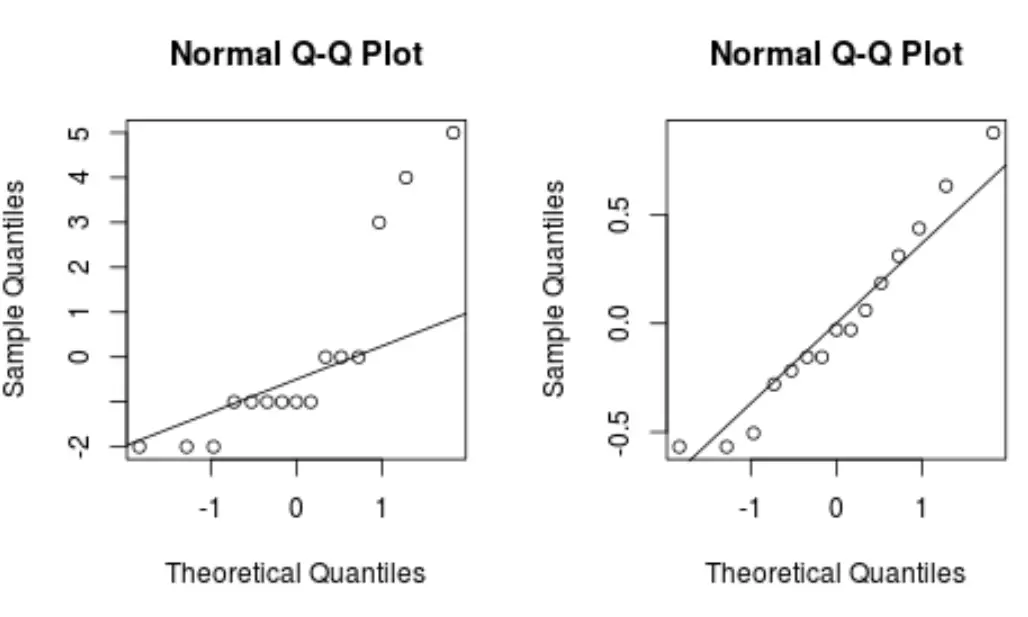
一般来说,如果数据点位于 QQ 图中的直线对角线上,则数据集可能服从正态分布。
请注意 box-cox 变换模型如何生成比原始回归模型更直的 QQ 图。
这表明 box-cox 变换模型的残差更加正态分布,满足 线性回归的假设之一。
其他资源
如何在 R 中转换数据(对数、平方根、立方根)
如何在 R 中创建和解释 QQ 图
如何在 R 中执行 Shapiro-Wilk 正态性检验