如何在 excel 中计算平均值的标准误差

平均值的标准误差是衡量数据集中值分布的一种方法。计算方法如下：

标准误差 = s / √n

金子：

• s ：样本标准差
• n ：样本量

您可以使用以下公式计算 Excel 中任何数据集平均值的标准误差：

= STDEV （值范围）/ SQRT （ COUNT （值范围））

以下示例展示了如何使用该公式。

示例：Excel 中的标准错误

假设我们有以下数据集：

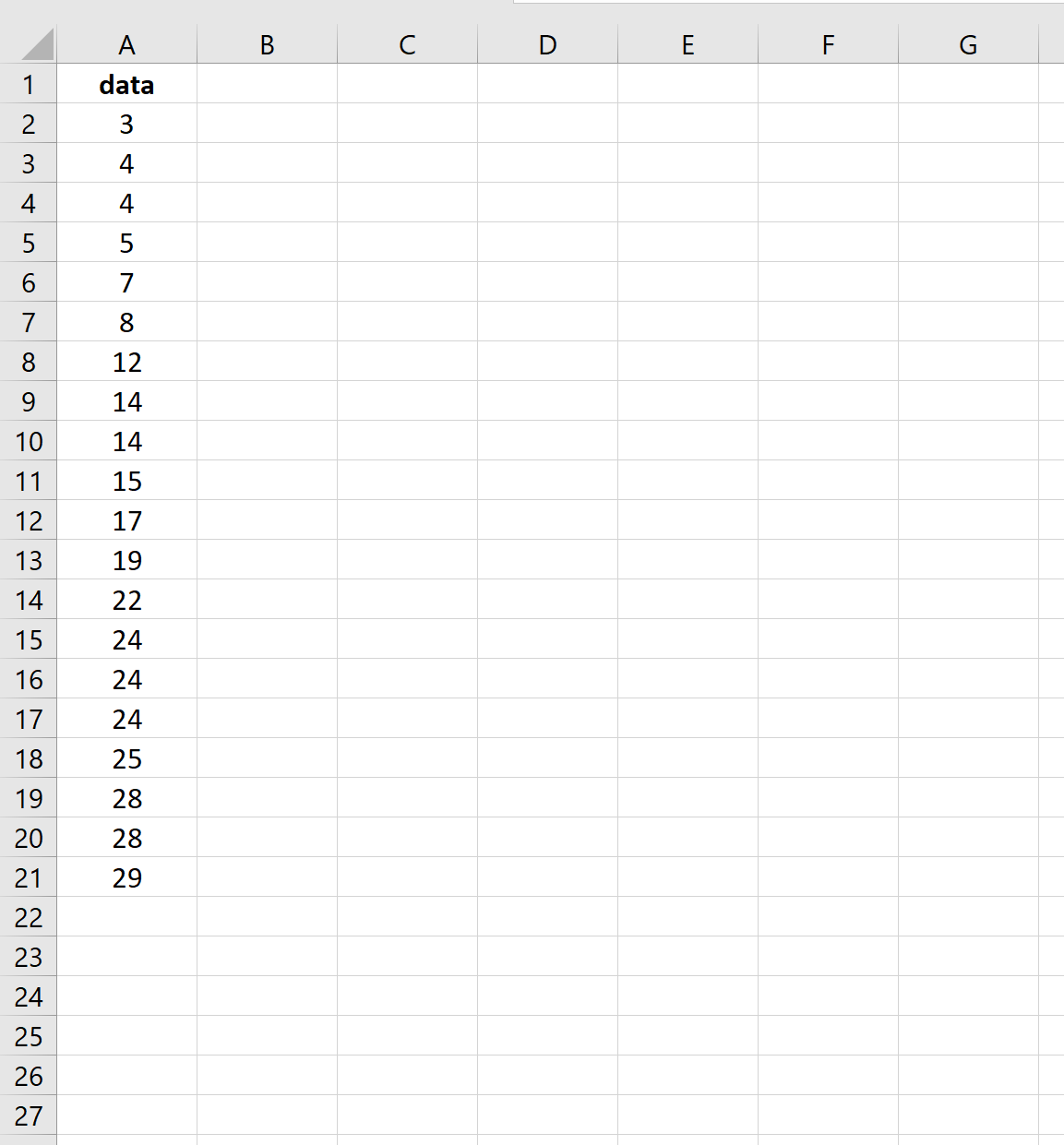
以下屏幕截图显示了如何计算该数据集平均值的标准误差：

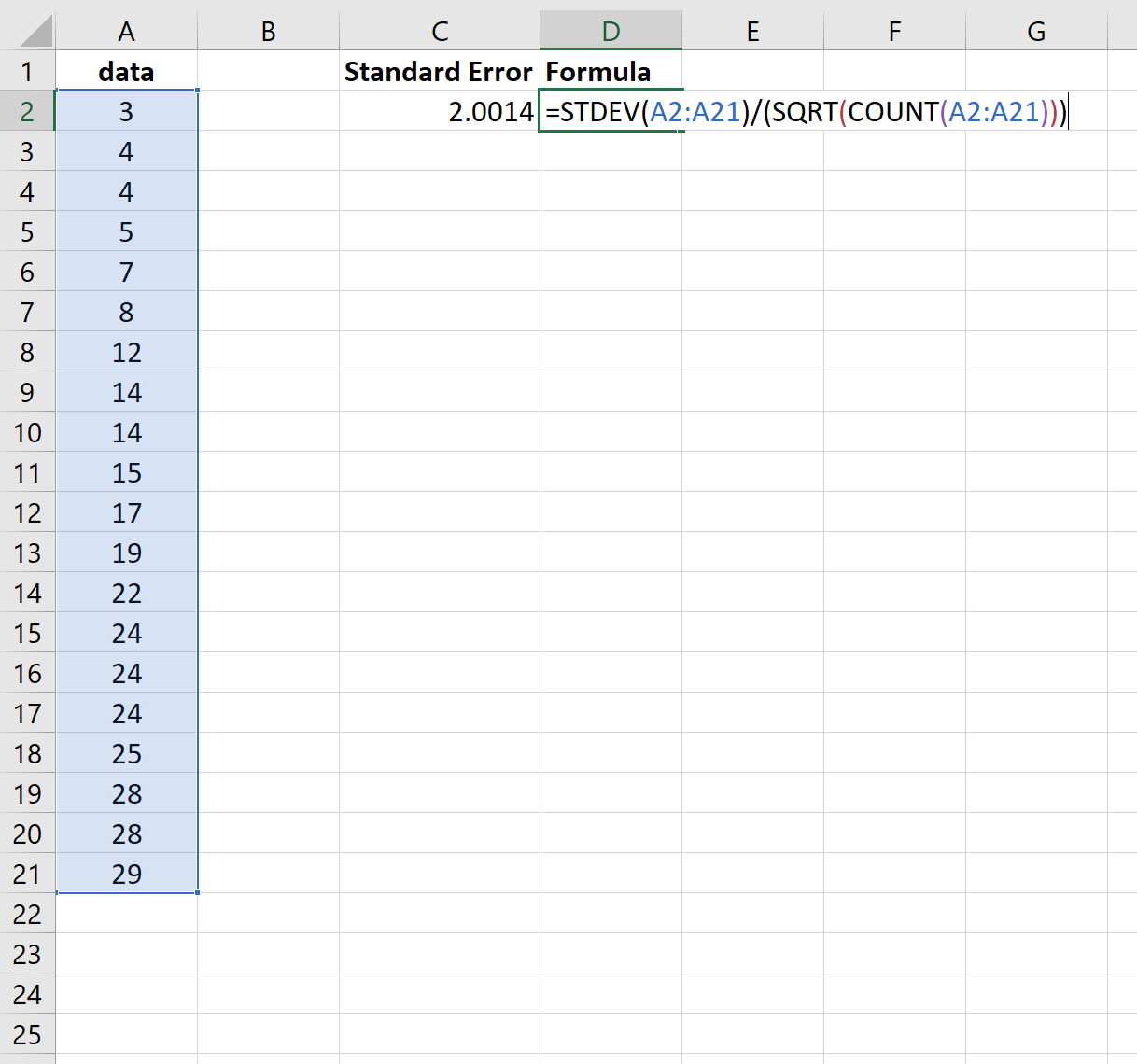
标准错误结果为2.0014 。

请注意， =STDEV()函数计算样本均值，这相当于 Excel 中的=STDEV.S()函数。

因此，我们可以使用以下公式来获得相同的结果：

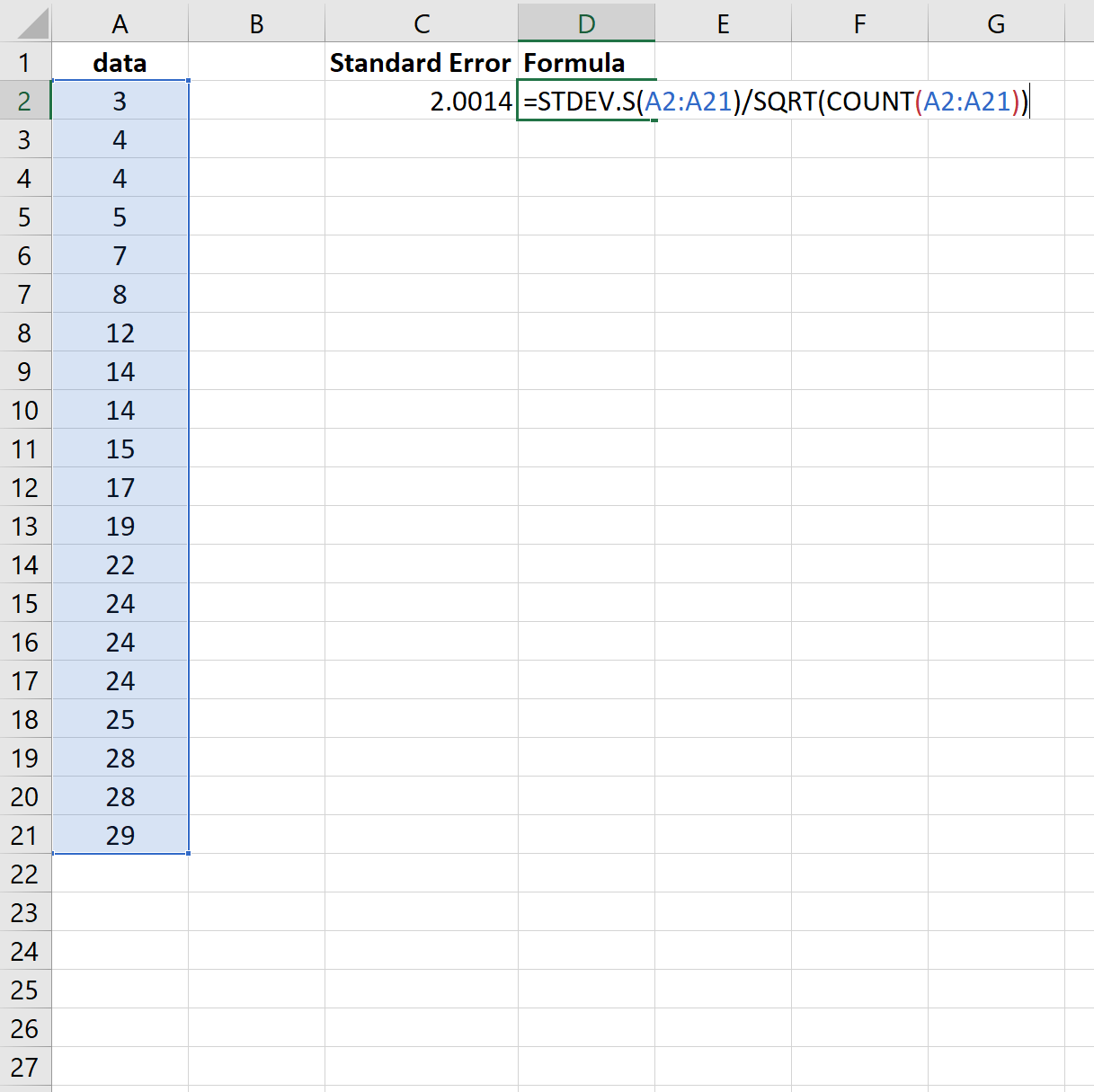
标准误差再次变为2.0014 。

如何解释平均值的标准误

均值的标准误差只是对均值周围值的分布的度量。解释平均值的标准误差时需要记住两件事：

1.均值的标准误差越大，数据集中的值在均值周围越分散。

为了说明这一点，考虑一下我们是否将前一个数据集的最后一个值更改了一个更大的数字：

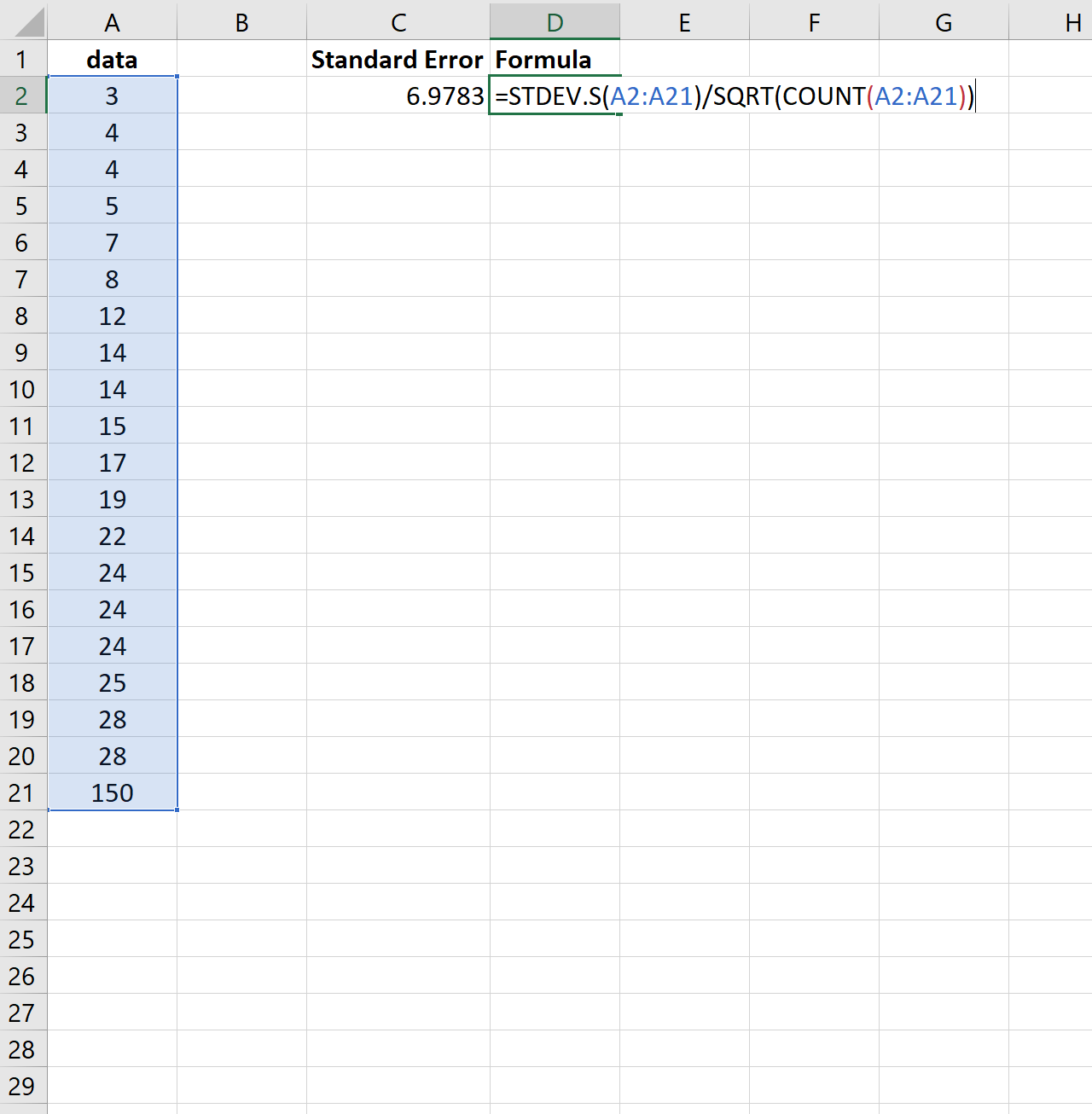
请注意标准误差如何从2.0014增加到6.9783 。这表明与之前的数据集相比，该数据集中的值更分布在平均值附近。

2.随着样本量的增加，平均值的标准误差趋于减小。

为了说明这一点，请考虑以下两组数据的平均值的标准误差：

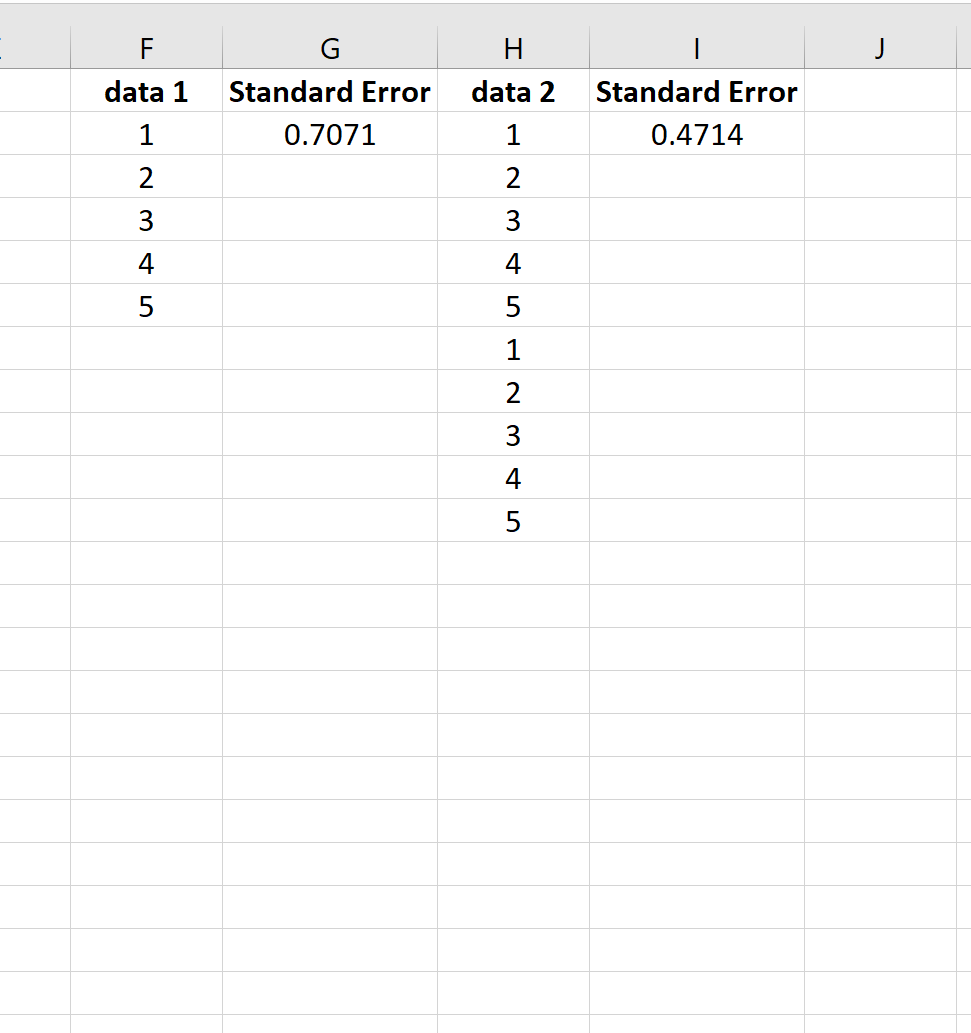
第二个数据集只是第一个数据集重复两次。因此，两个数据集具有相同的均值，但第二个数据集的样本量较大，因此标准误差较小。