如何在 excel 中创建和解释相关矩阵
量化两个变量之间关系的一种方法是使用Pearson 相关系数,它是两个变量之间线性关联的度量。
它的值介于 -1 和 1 之间,其中:
- -1 表示两个变量之间完全负线性相关
- 0 表示两个变量之间不存在线性相关
- 1 表示两个变量之间存在完全正线性相关
相关系数离零越远,两个变量之间的相关性越强。
但在某些情况下,我们想要了解多对变量之间的相关性。
在这些情况下,我们可以创建一个相关矩阵,它是一个方表,显示变量的多个成对组合之间的相关系数。
本教程介绍如何在 Excel 中创建和解释相关矩阵。
如何在 Excel 中创建相关矩阵
假设我们有以下数据集,显示 10 名篮球运动员的平均得分、篮板和助攻数:
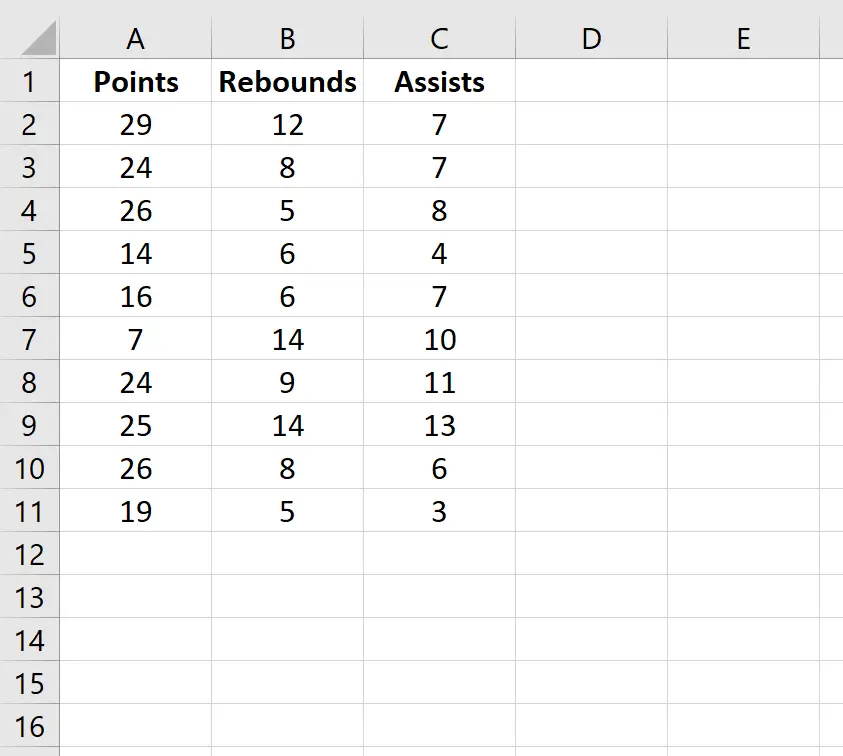
要为此数据集创建相关矩阵,请转到 Excel 顶部功能区中的“数据”选项卡,然后单击“数据分析” 。

如果您没有看到此选项,则必须首先在 Excel 中加载免费的数据分析工具库。
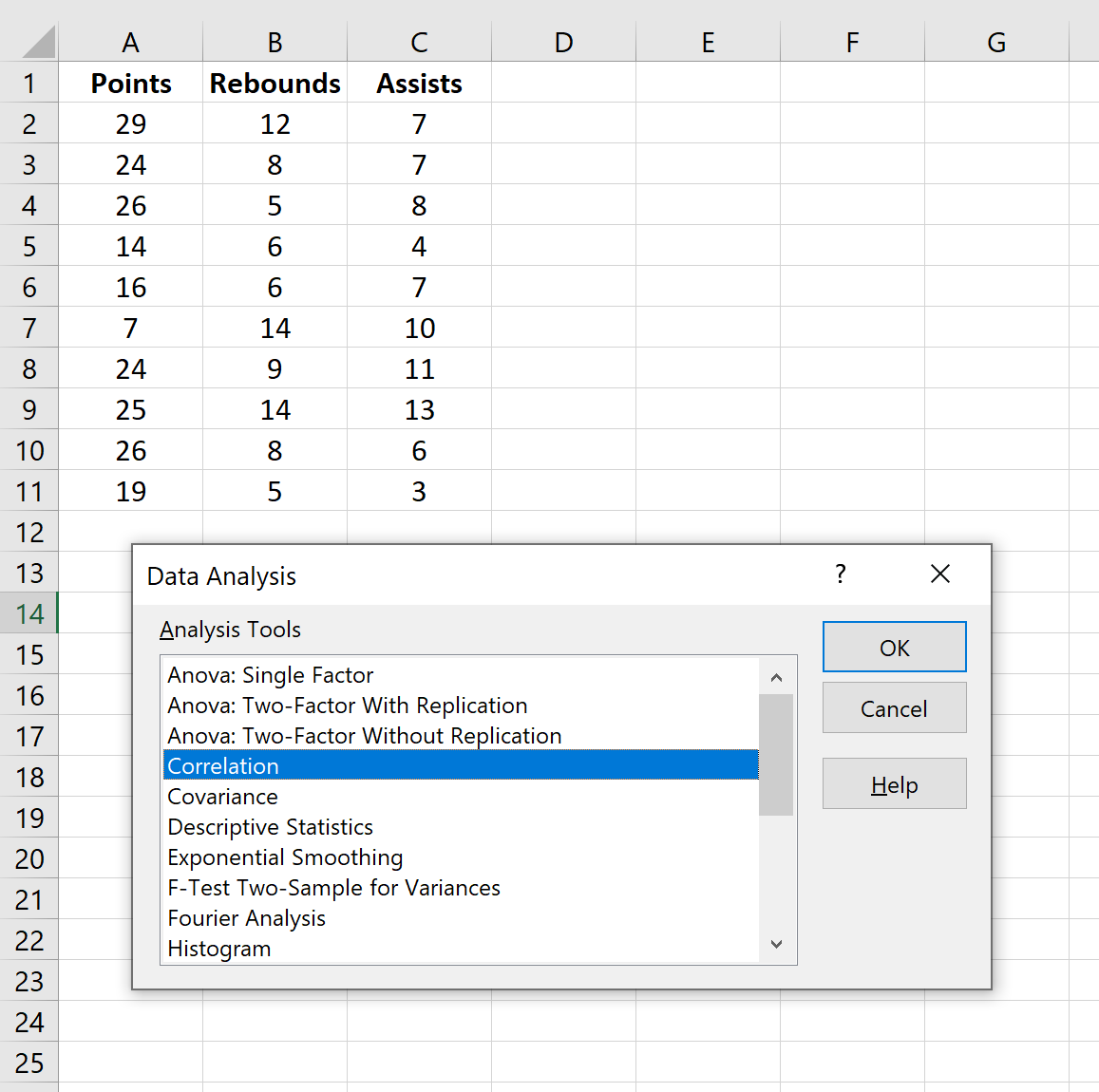
在出现的新窗口中,选择“相关性”并单击“确定” 。
对于输入范围,选择数据所在的单元格(包括带标签的第一行)。选中第一行标签旁边的框。对于输出范围,选择您想要显示相关矩阵的单元格。然后单击“确定” 。
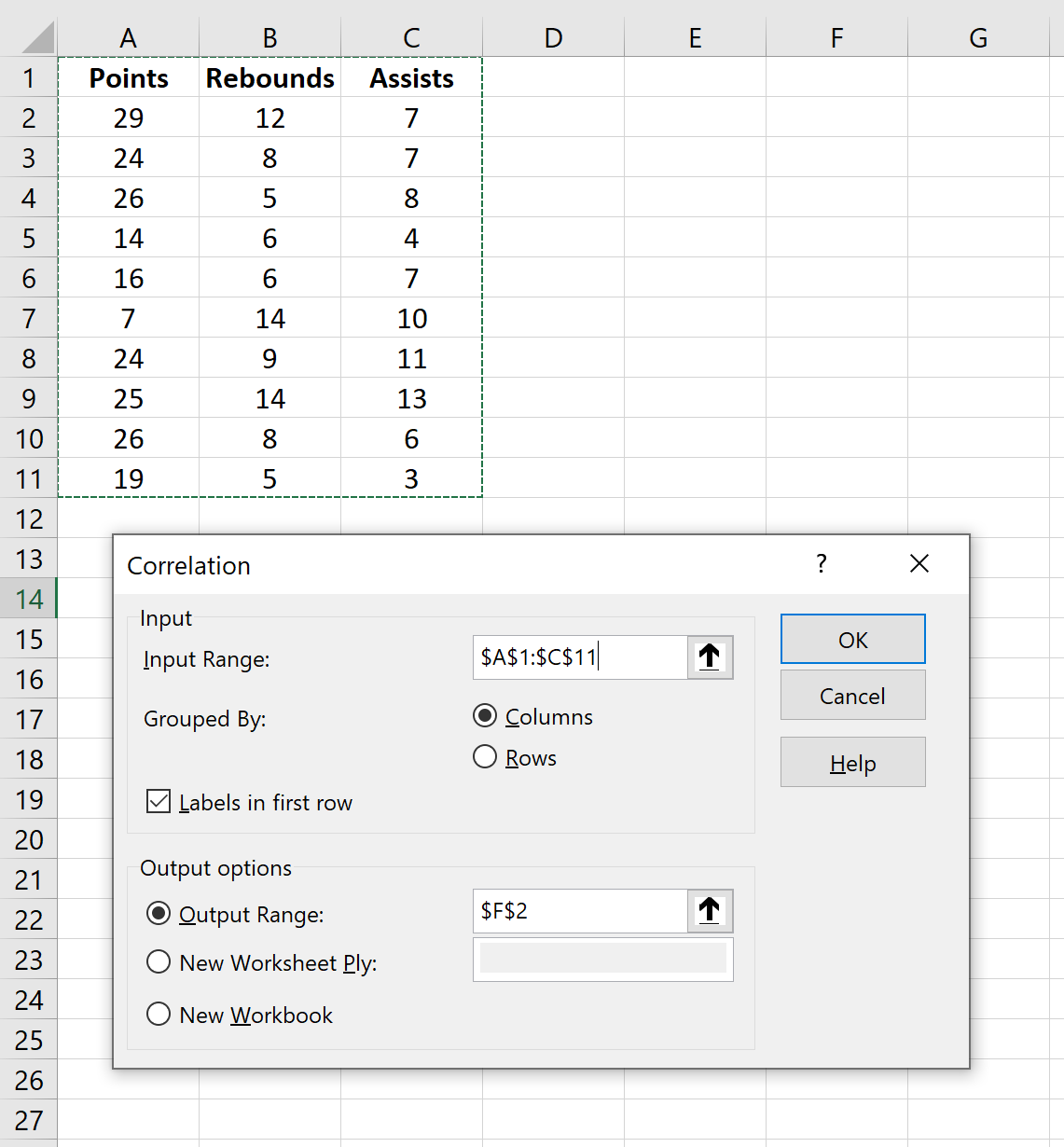
这将自动生成以下相关矩阵:
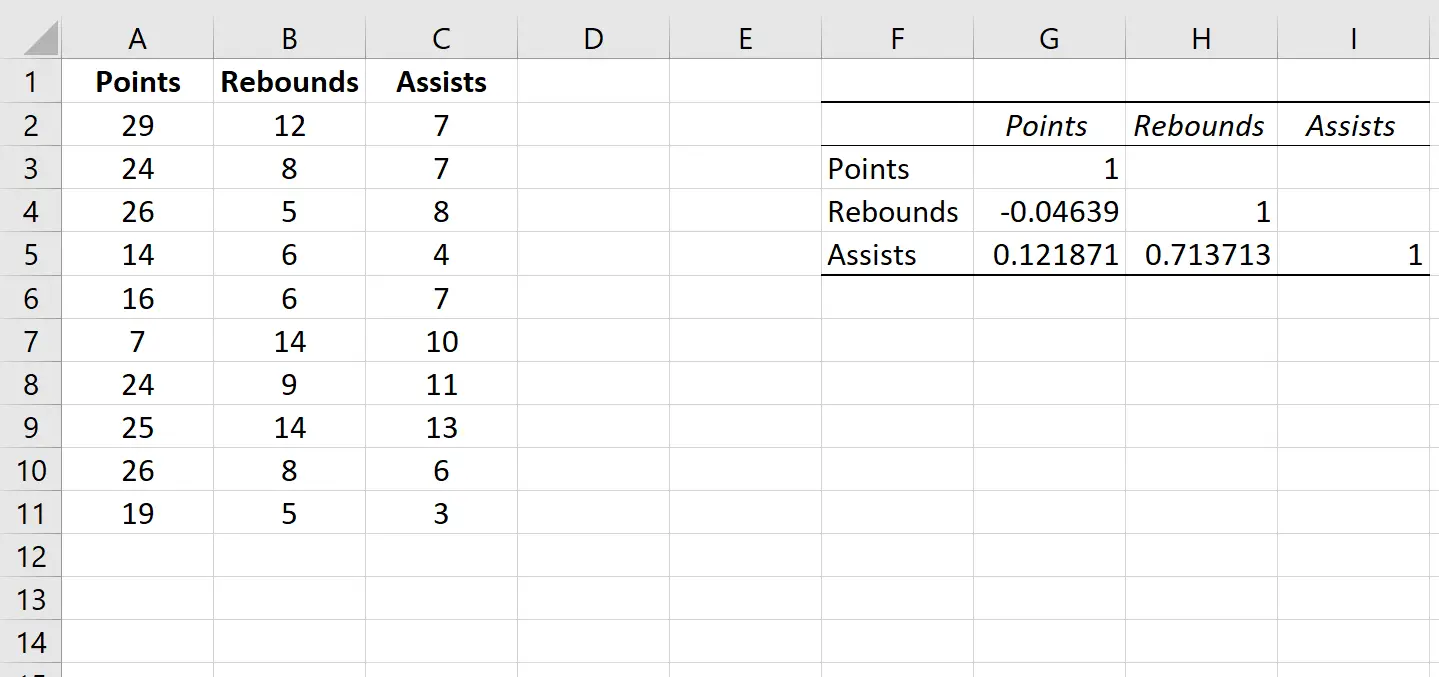
如何在 Excel 中解释相关矩阵
相关矩阵各个单元格中的值告诉我们每个变量成对组合之间的皮尔逊相关系数。例如:
得分和篮板之间的相关性: -0.04639。得分和篮板略有负相关,但该值非常接近于零,以至于没有强有力的证据表明这两个变量之间存在显着关联。
得分和助攻之间的相关性: 0.121871。得分和助攻略有正相关,但这个值也非常接近于零,因此没有强有力的证据表明这两个变量之间存在显着关联。
篮板和助攻之间的相关性: 0.713713。篮板球和助攻呈强正相关。也就是说,拥有更多篮板的球员往往也有更多的助攻。
请注意,相关矩阵的对角线值全部为 1,因为变量与其自身之间的相关性始终为 1。在实践中,这个数字对于解释没有什么用处。
奖励:可视化相关系数
可视化表中相关系数值的一种简单方法是对表应用条件格式。
在 Excel 的顶部功能区上,转到“开始”选项卡,然后转到“样式”组。
单击“条件格式图表” 、 “色阶” 、 “绿-黄-红色阶” 。
这会自动将以下色标应用于相关矩阵:
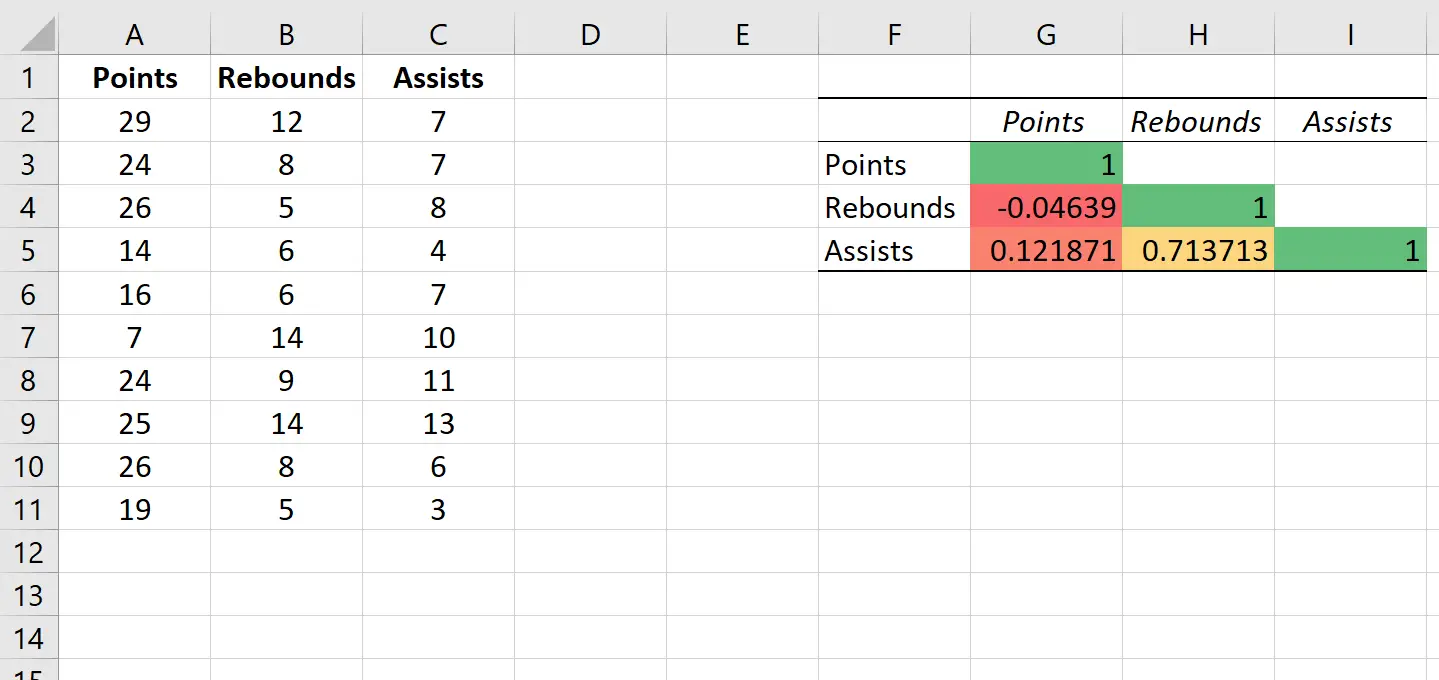
这有助于我们轻松地可视化变量之间相关性的强度。
如果我们使用具有许多变量的相关矩阵,这是一个特别有用的技巧,因为它可以帮助我们快速识别具有最强相关性的变量。
其他资源
以下教程解释了如何在 R 中执行其他常见任务: