如何在 excel 中计算均方根误差 (rmse)

在统计学中， 回归分析是一种用于理解预测变量 x 和响应变量 y 之间关系的技术。

当我们进行回归分析时，我们得到一个模型，它根据预测变量的值告诉我们响应变量的预测值。

评估我们的模型对给定数据集的拟合程度的一种方法是计算均方误差，这是一个指标，可以告诉我们预测值与观测值的平均差距有多大。

求均方误差（通常称为RMSE ）的公式为：

RMSE = √[ Σ(P _i – O _i ) ² / n ]

金子：

• Σ 是一个奇特的符号，意思是“和”
• P _i是数据集中^{第 i 个}观测值的预测值
• O _i是数据集中^{第 i 个}观测值的观测值
• n 是样本量

技术说明：

• 可以计算产生预测值的任何类型的模型的均方误差，然后可以将其与数据集的观测值进行比较。
• 均方误差有时也称为均方偏差，通常缩写为 RMSD。

接下来，让我们看一下如何在 Excel 中计算均方误差的示例。

如何在 Excel 中计算均方误差

Excel中没有内置函数来计算RMSE，但我们可以通过一个公式轻松计算它。我们将展示如何计算两种不同场景的 RMSE。

场景1

在一种场景中，您可以有一列包含模型的预测值，另一列包含观测值。下图显示了此场景的示例：

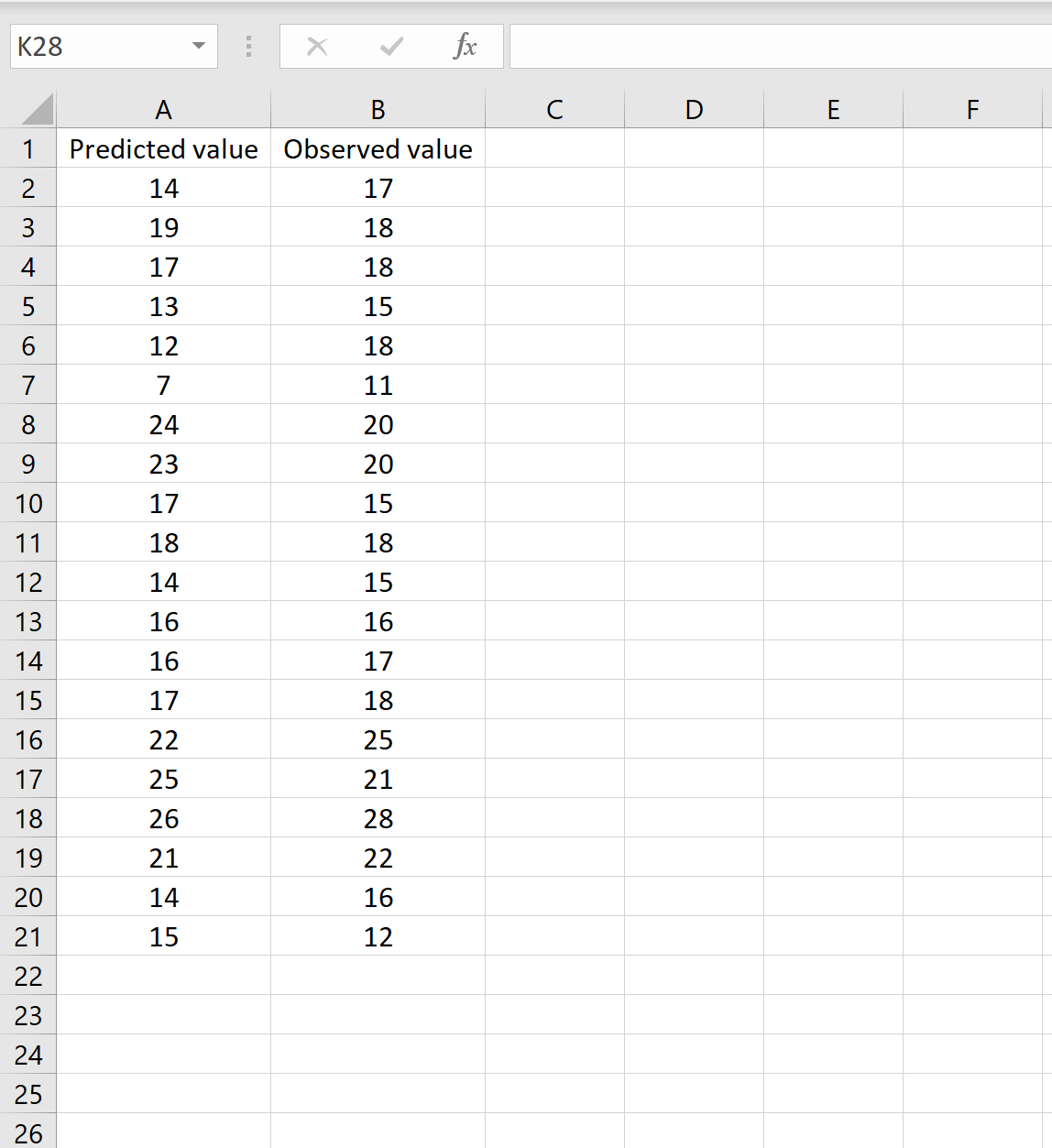
如果是这样，您可以通过在任意单元格中键入以下公式，然后单击 CTRL+SHIFT+ENTER 来计算 RMSE：

=SQRT(SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21))

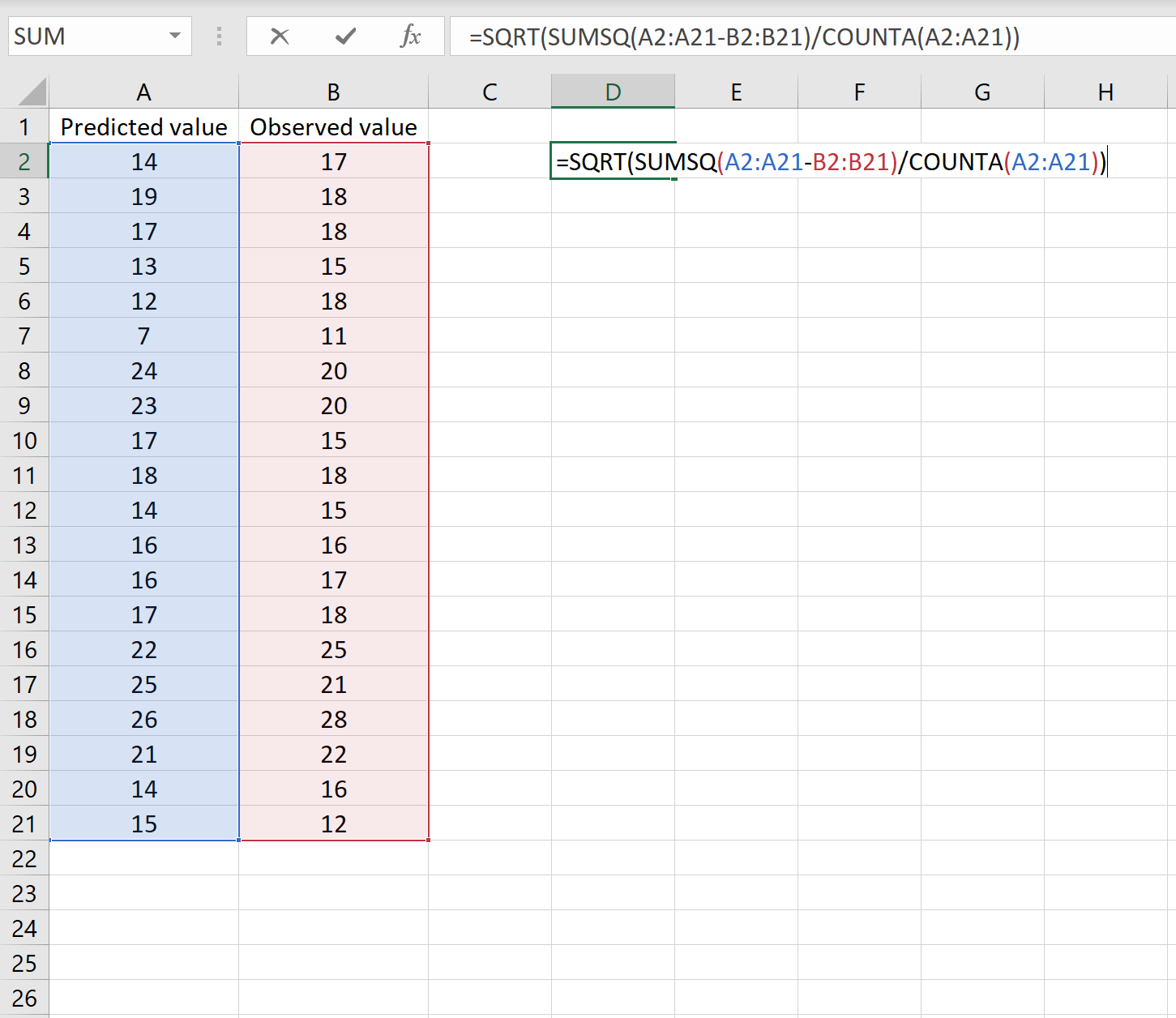
这告诉我们均方误差为2.6646 。

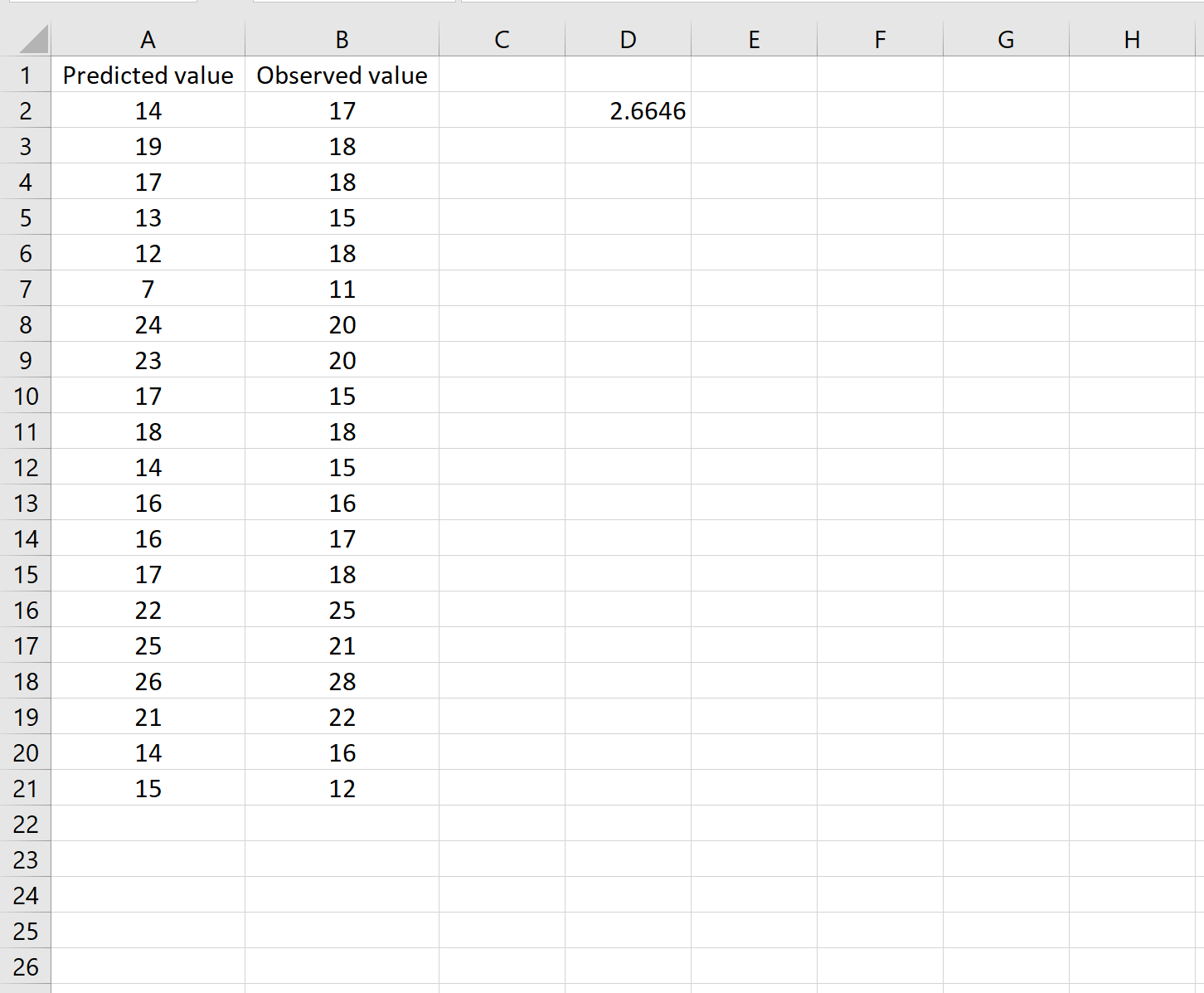
这个公式可能看起来有点棘手，但是一旦你分解它就很有意义：

= SQRT( SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21) )

• 首先，我们使用SUMSQ()函数计算预测值和观测值之间差异的平方和。
• 接下来，我们使用COUNTA()除以数据集的样本大小，这会计算区域中非空单元格的数量。
• 最后，我们使用SQRT()函数对整个计算求平方根。

场景2

在另一种情况下，您可能已经计算了预测值和观测值之间的差异。在这种情况下，您将只有一列显示差异。

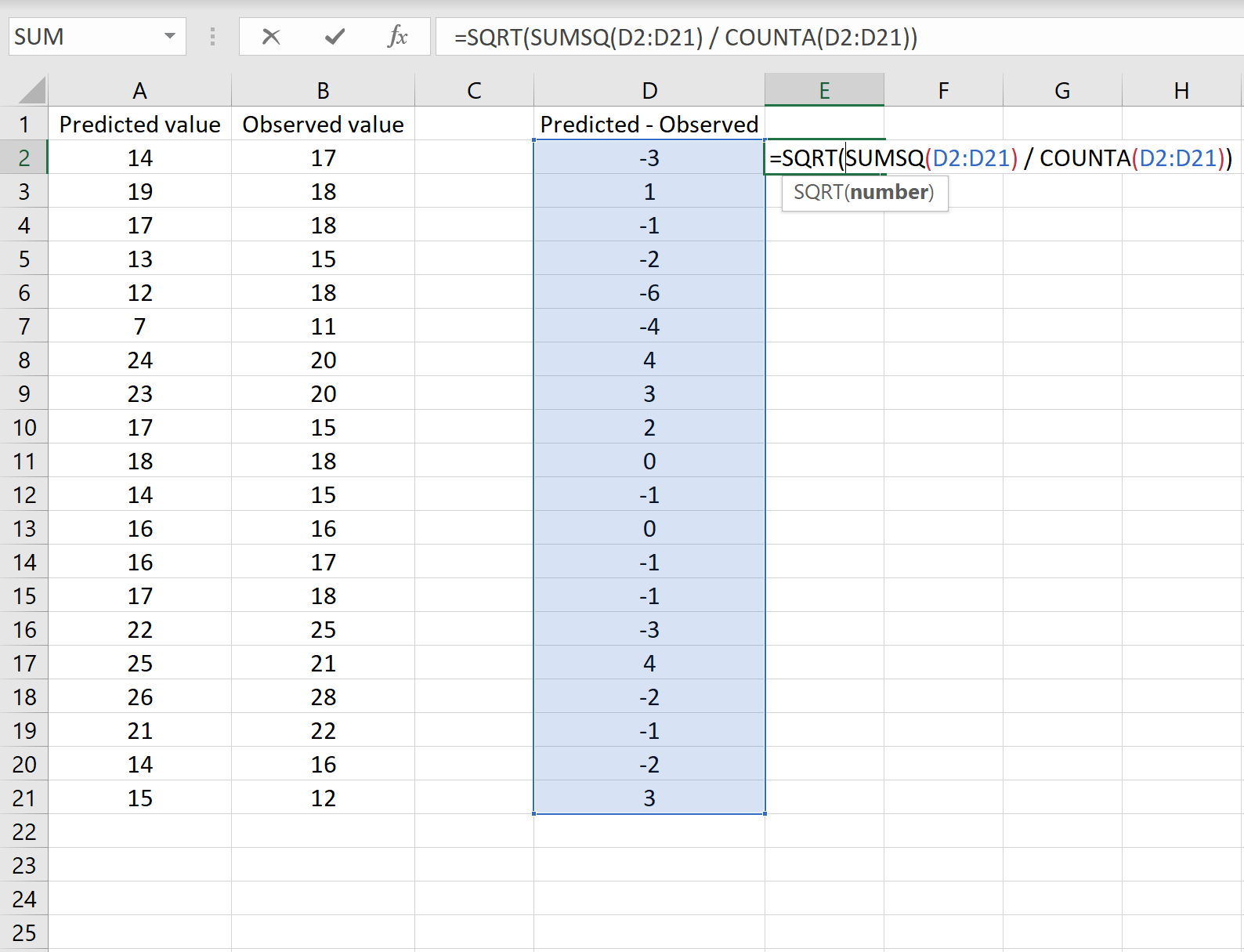
下图显示了此场景的示例。预测值显示在 A 列中，观测值显示在 B 列中，预测值与观测值之间的差值显示在 D 列中：

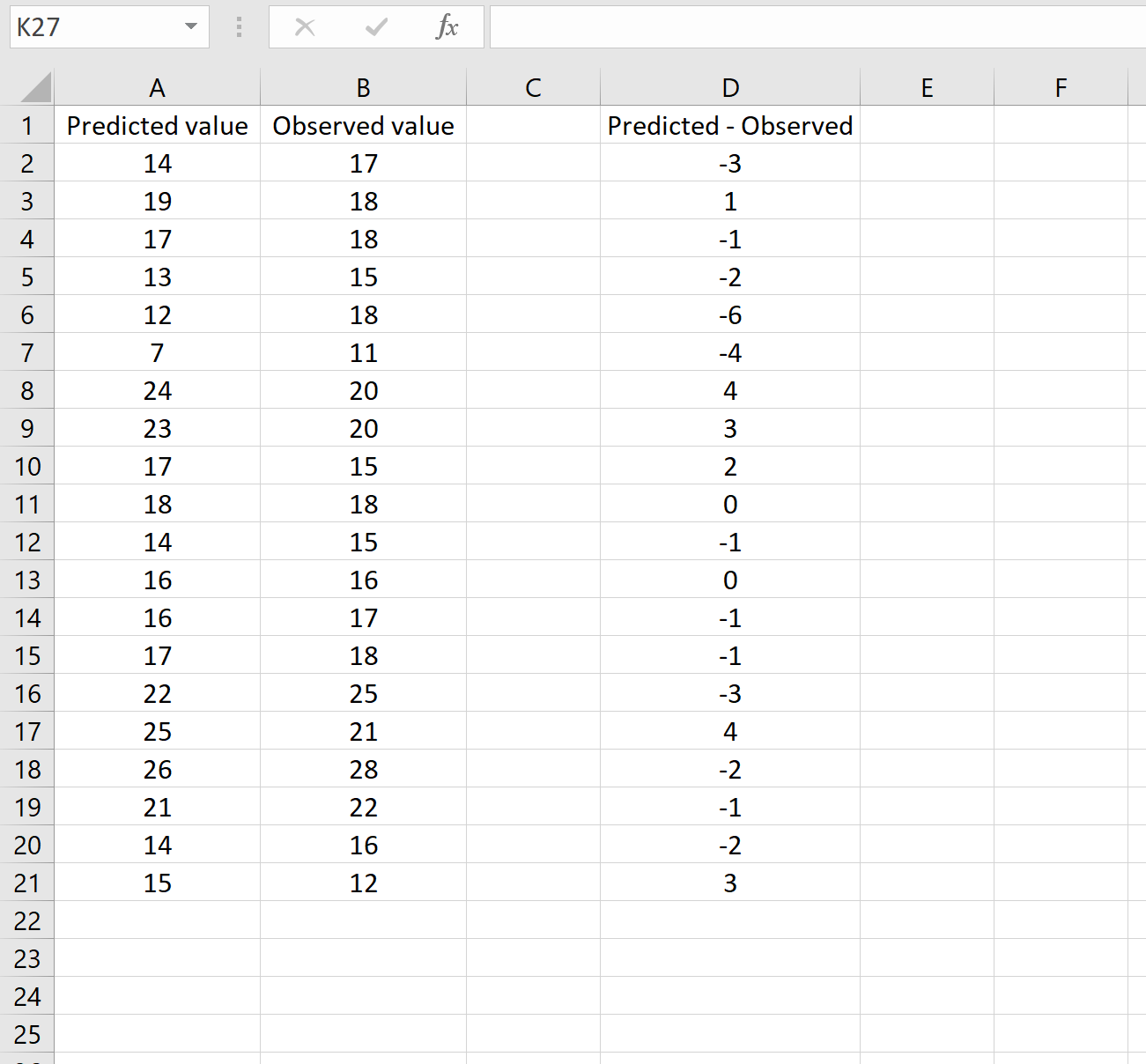
如果是这样，您可以通过在任意单元格中键入以下公式，然后单击 CTRL+SHIFT+ENTER 来计算 RMSE：

=SQRT(SUMSQ(D2:D21) / COUNT(D2:D21))

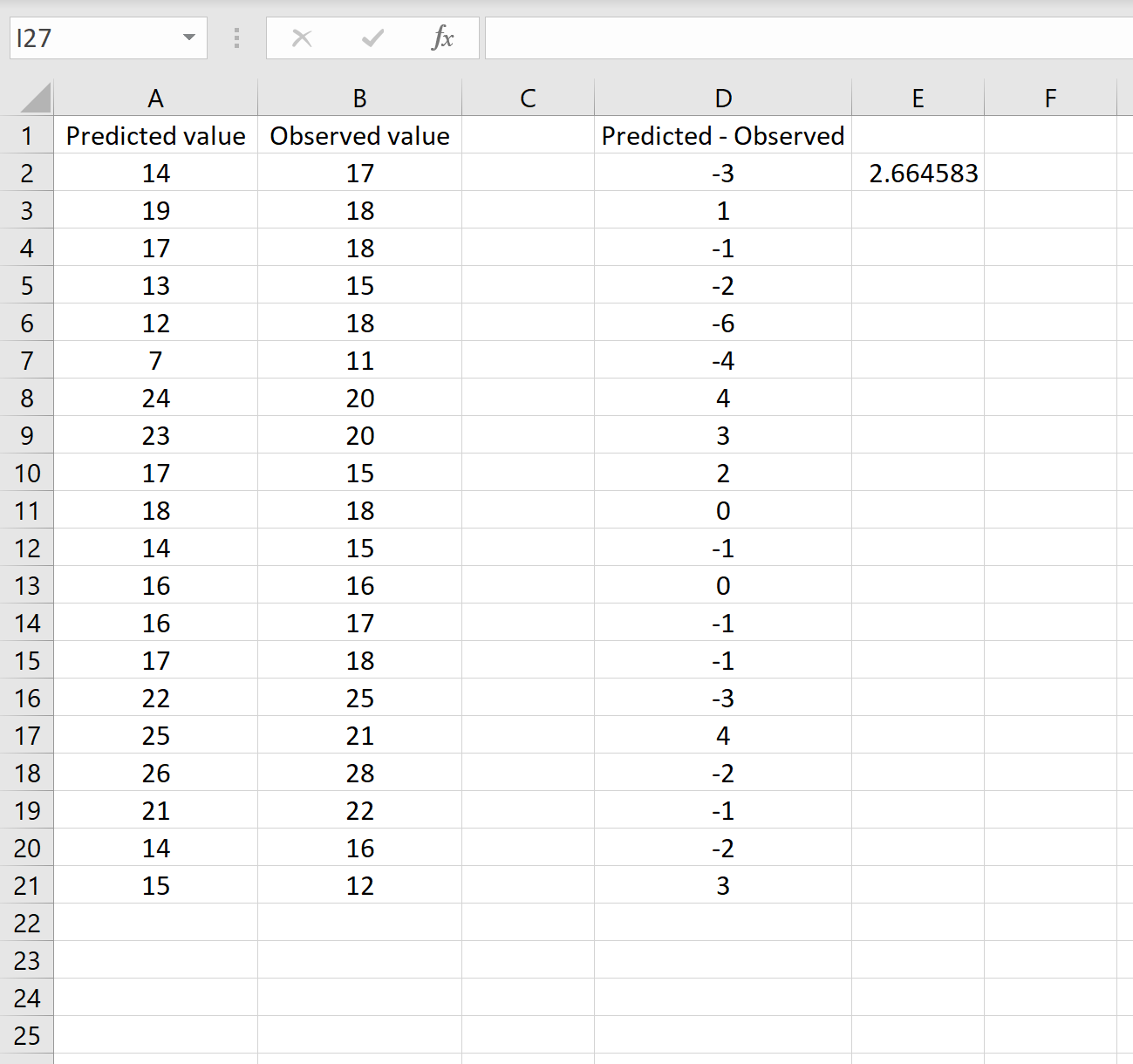
这告诉我们均方误差为2.6646 ，对应于第一种情况下获得的结果。这证实了这两种计算 RMSE 的方法是等效的。

我们在此场景中使用的公式与我们在之前场景中使用的公式仅略有不同：

= SQRT( SUMSQ(D2:D21) / COUNT(D2:D21) )

• 由于我们已经计算了 D 列中的预测值和观测值之间的差异，因此我们可以使用 SUMSQ() 函数计算差异平方和。  仅使用 D 列中的值的函数。
• 接下来，我们使用COUNTA()除以数据集的样本大小，这会计算区域中非空单元格的数量。
• 最后，我们使用SQRT()函数对整个计算求平方根。

如何解释 RMSE

如前所述， RMSE是查看回归模型（或任何生成预测值的模型）“拟合”数据集的能力的有用方法。

RMSE 越大，预测值和观测值之间的差异越大，意味着回归模型对数据的拟合程度越差。相反，RMSE 越小，模型对数据的拟合效果越好。

比较两个不同模型的 RMSE 以了解哪个模型最适合数据尤其有用。

有关 Excel 的更多教程，请务必查看我们的Excel 指南页面，其中列出了所有有关统计的 Excel 教程。