Excel 中的曲线拟合（附示例）

通常，您可能希望找到最适合 Excel 中一组数据的曲线的方程。

幸运的是，使用 Excel 的趋势线函数可以非常简单地做到这一点。

本教程提供了如何在 Excel 中将方程拟合为曲线的分步示例。

第 1 步：创建数据

首先，让我们创建一个假数据集来使用：

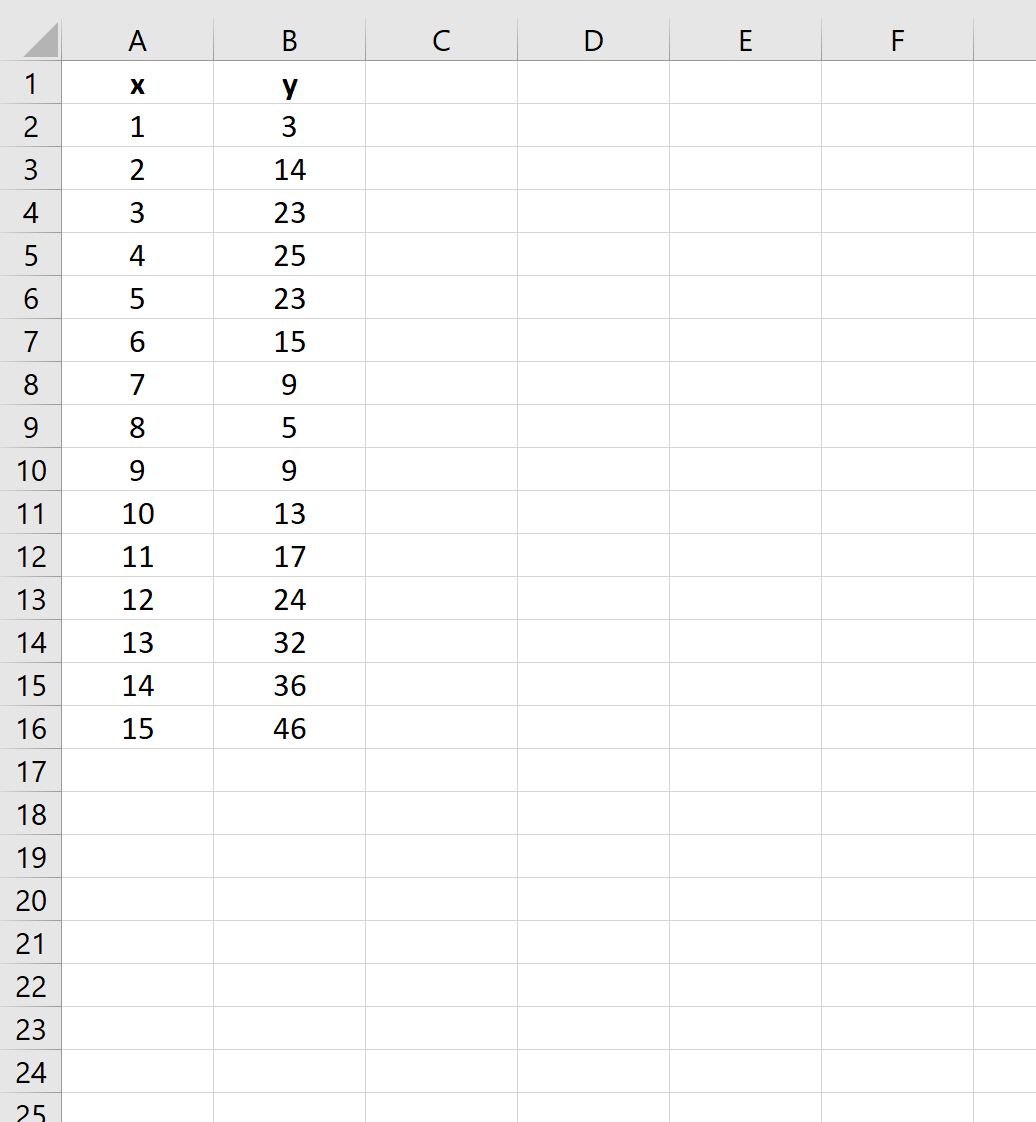
第 2 步：创建散点图

接下来，我们创建一个散点图来可视化数据集。

首先，突出显示单元格A2:B16 ，如下所示：

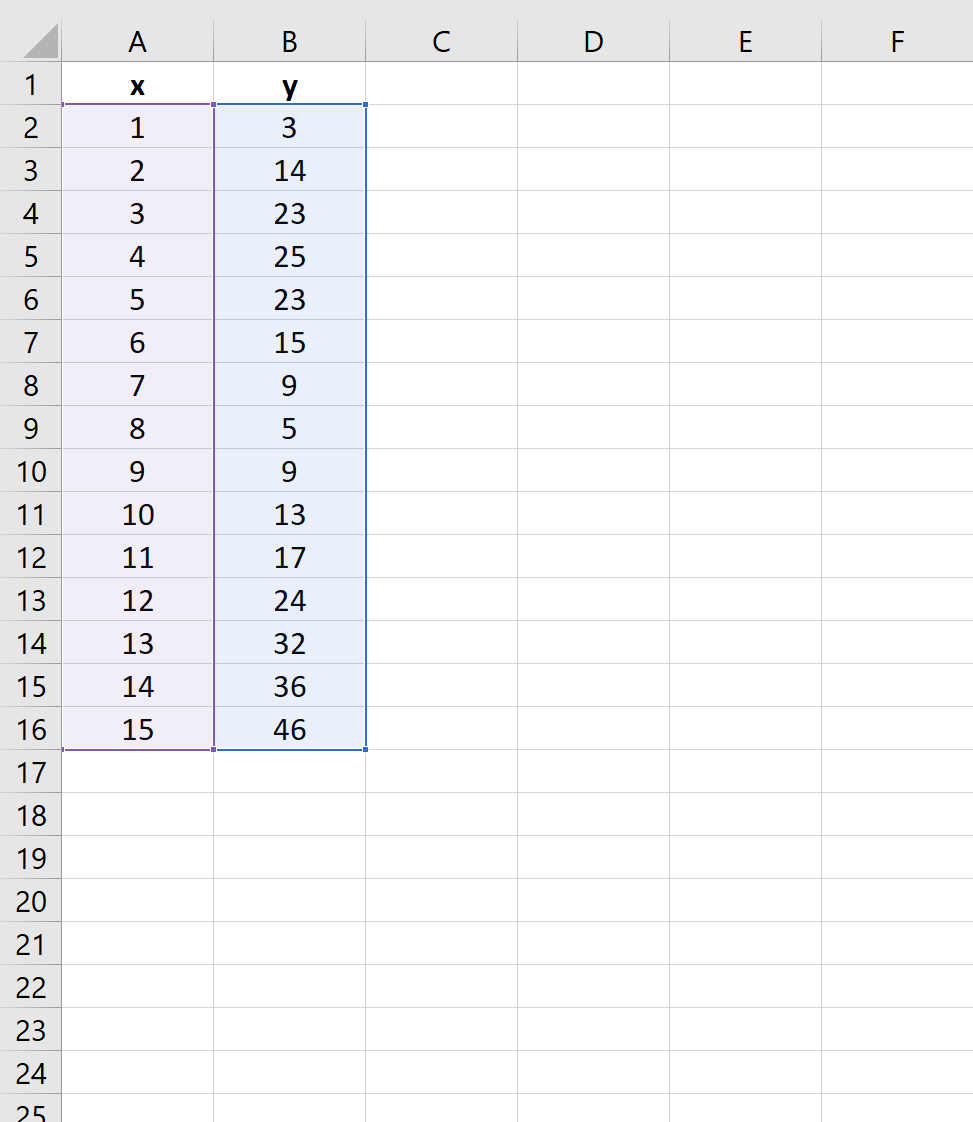
接下来，单击顶部功能区的“插入”选项卡，然后单击“散点图”下的第一个绘图选项：

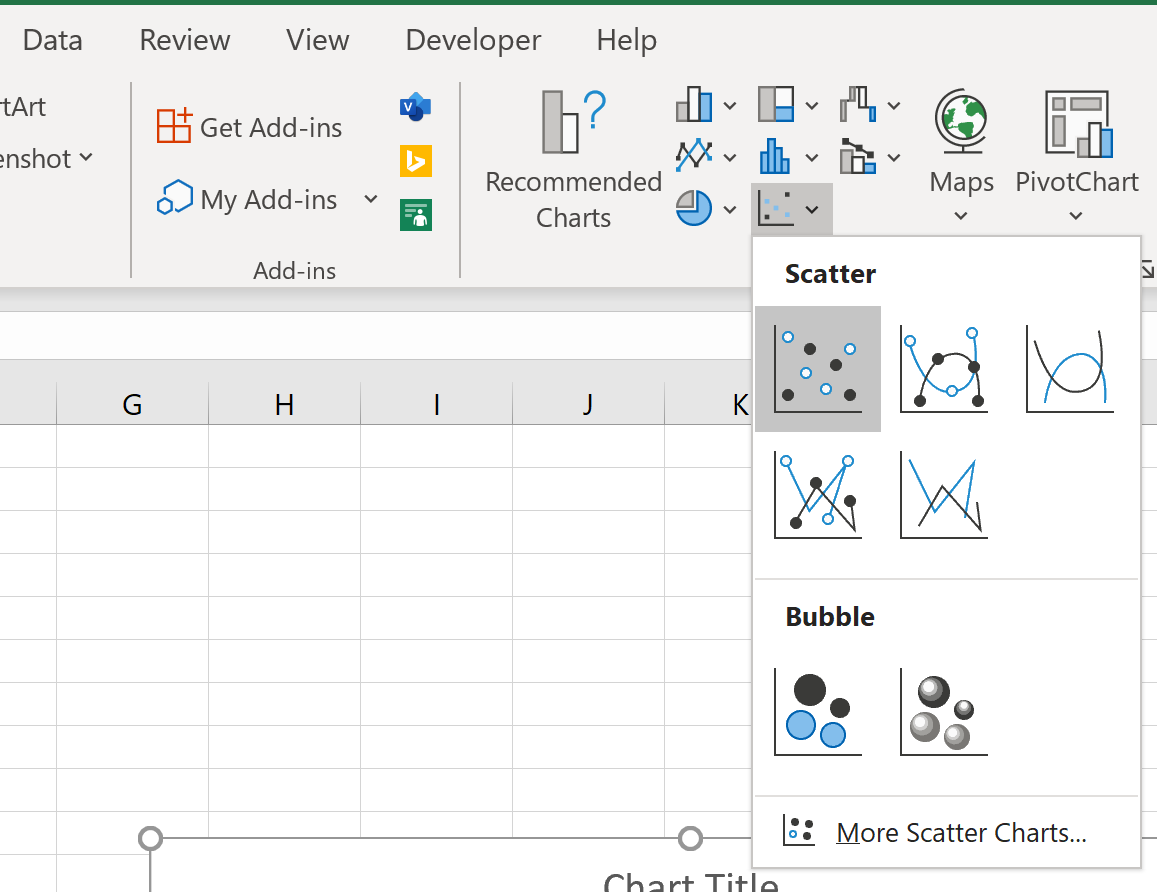
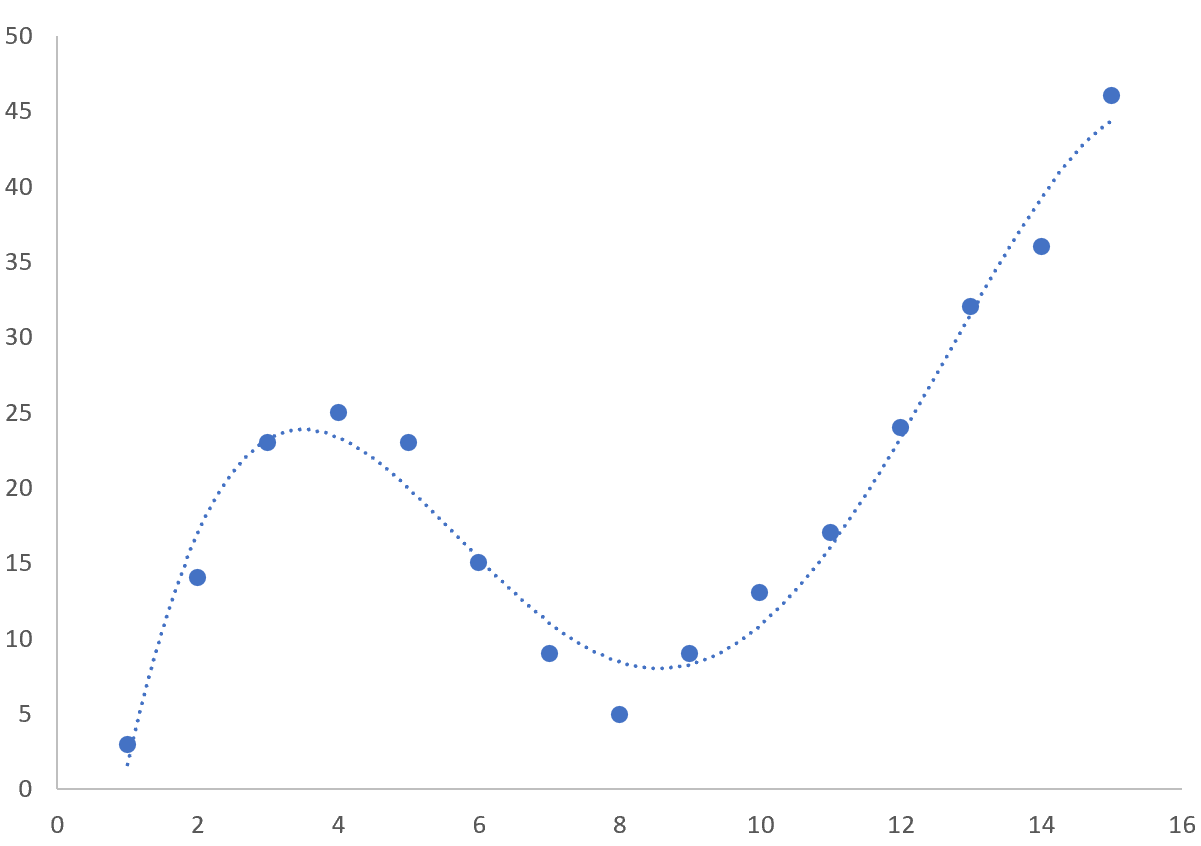
这会产生以下散点图：

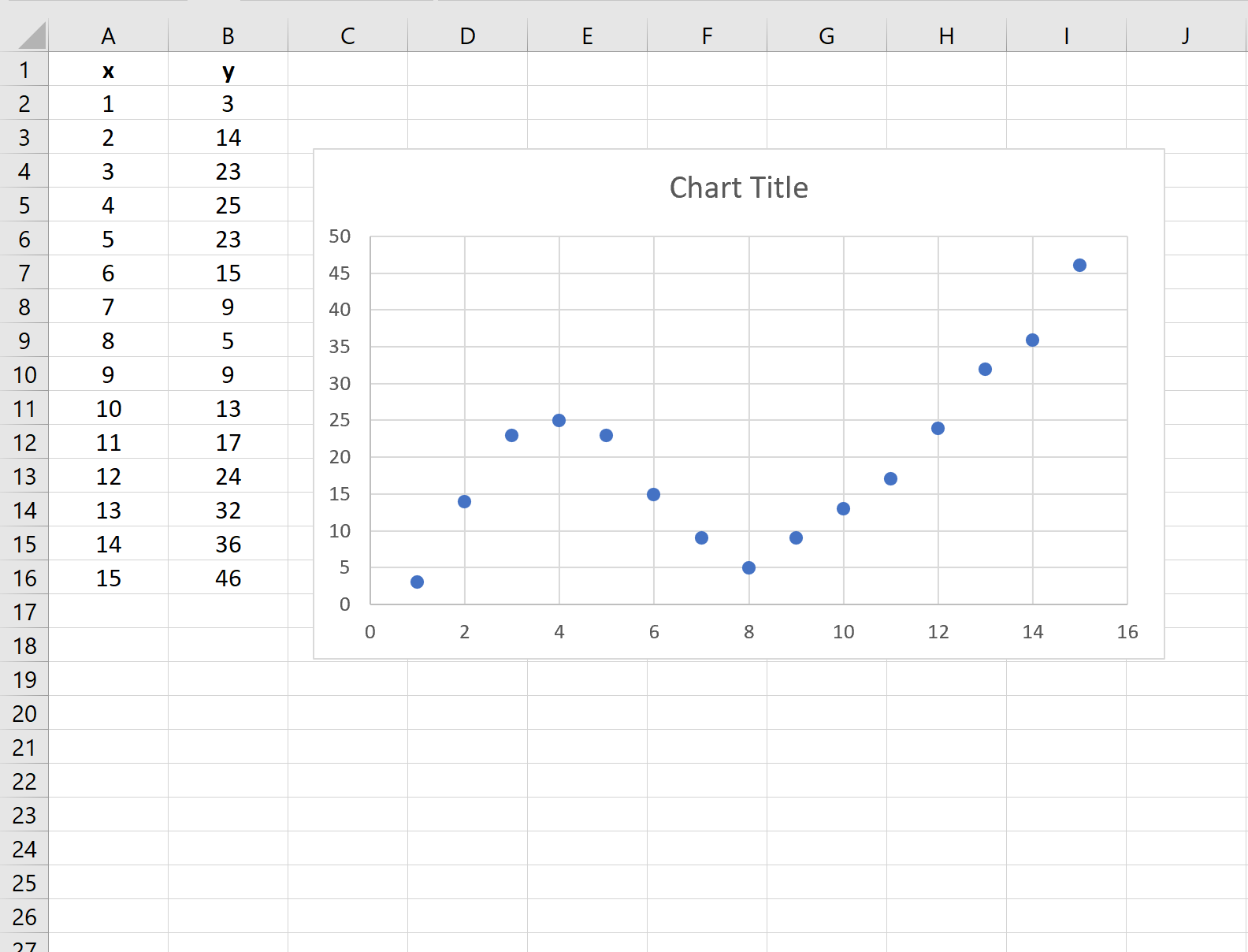
第 3 步：添加趋势线

接下来，单击散点图上的任意位置。然后点击右上角的+号。在下拉菜单中，单击趋势线旁边的箭头，然后单击更多选项：

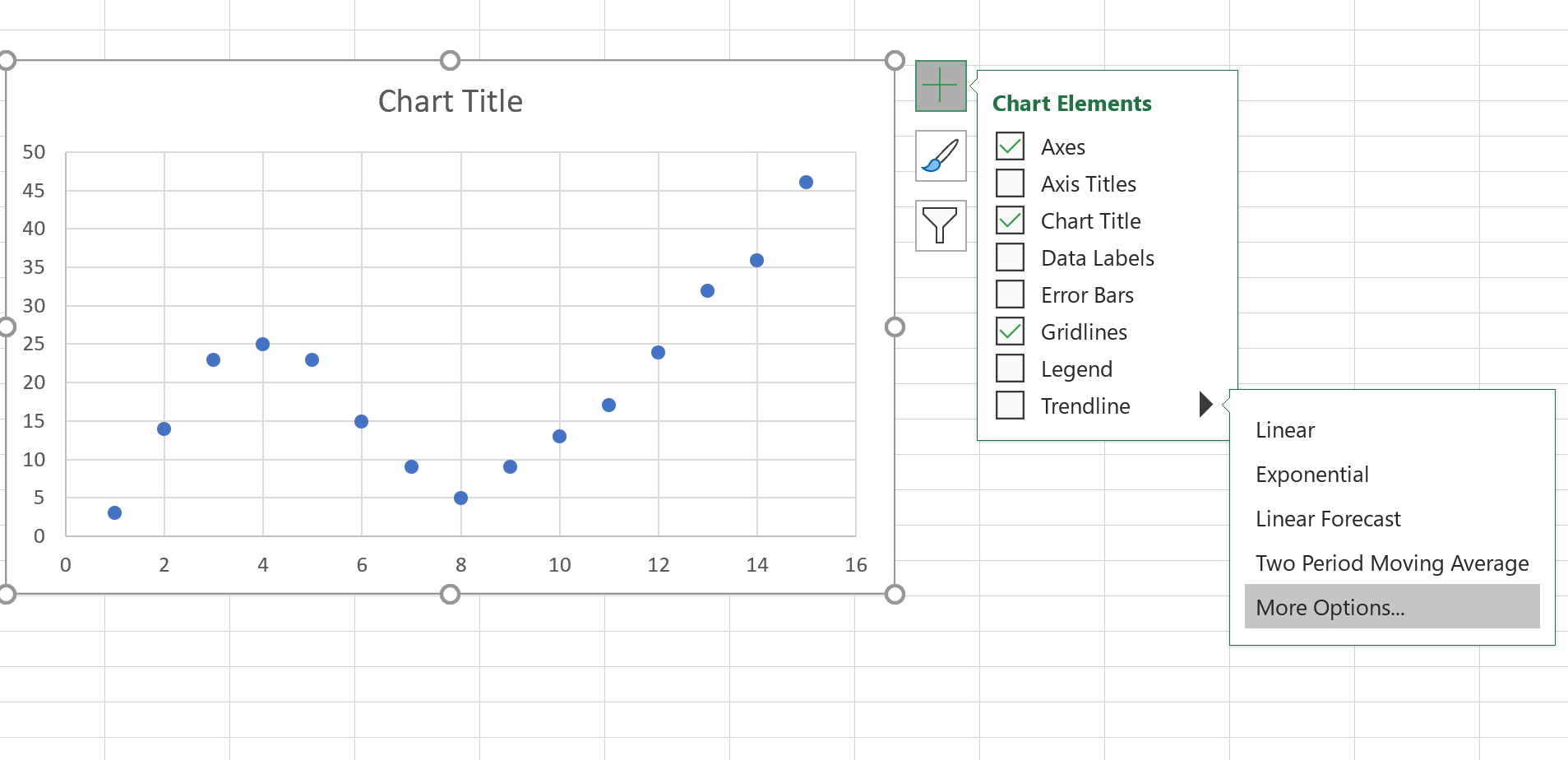
在右侧出现的窗口中，单击Polynomial旁边的按钮。然后选中“在图表上显示方程”和“在图表上显示 R 平方值”旁边的框。

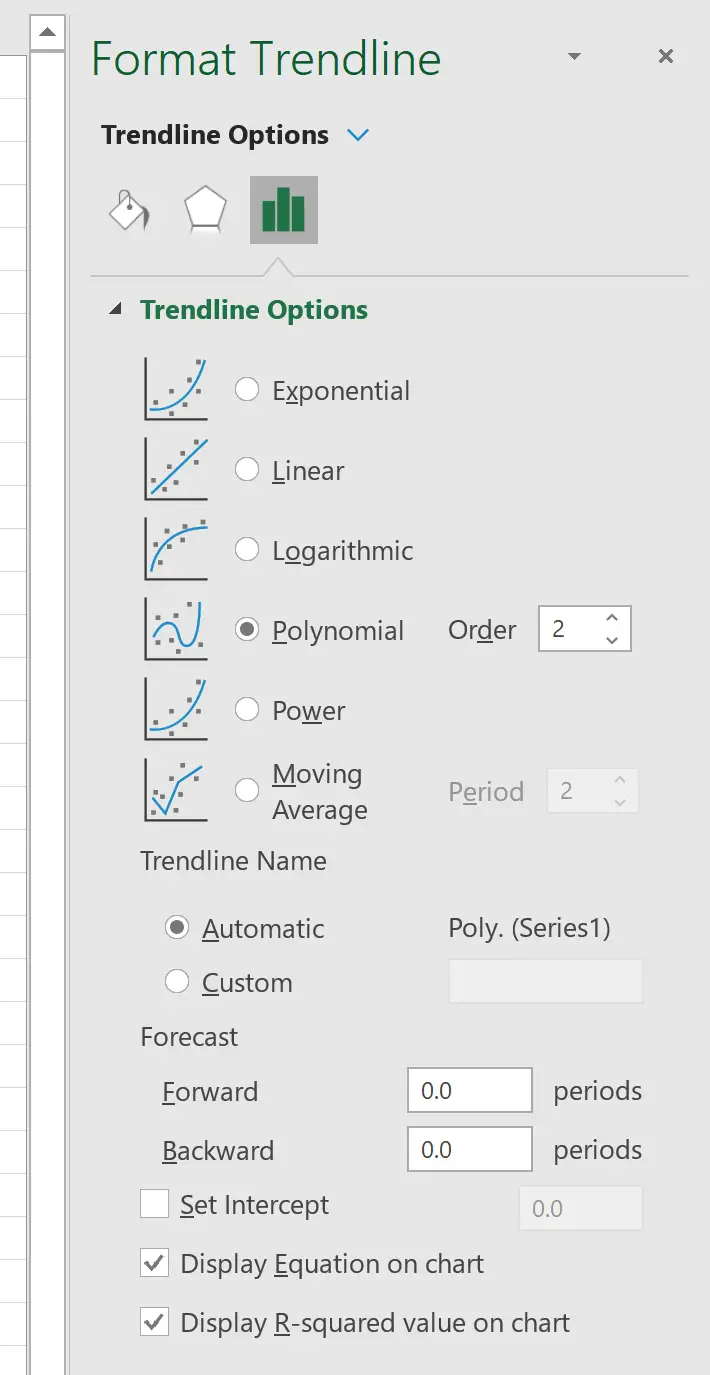
这会在点云上产生以下曲线：

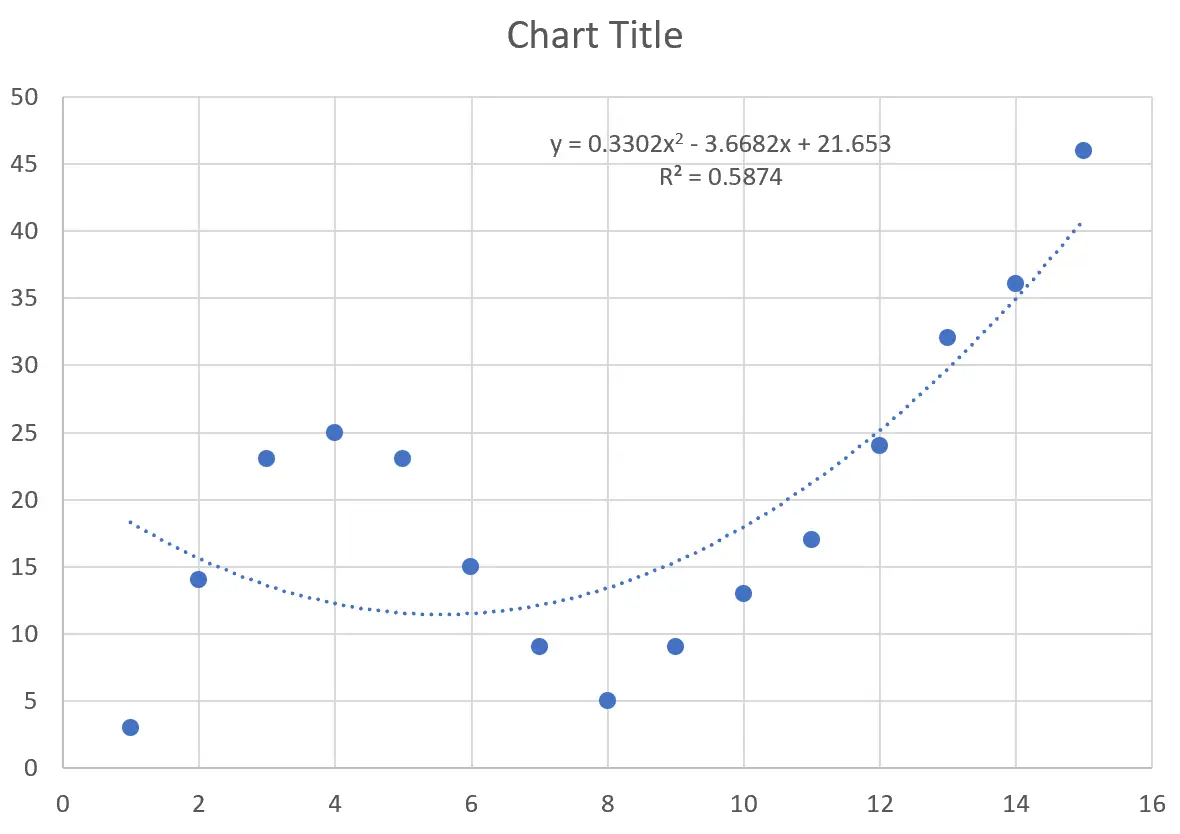
曲线方程如下：

y = 0.3302x ² – 3.6682x + 21.653

R 平方告诉我们可以由预测变量解释的响应变量的变化百分比。该特定曲线的 R 平方为0.5874 。

第四步：选择最佳趋势线

我们还可以增加所使用的多项式的阶数，以查看更灵活的曲线是否可以更好地拟合数据集。

例如，我们可以选择将多项式阶数设置为 4：

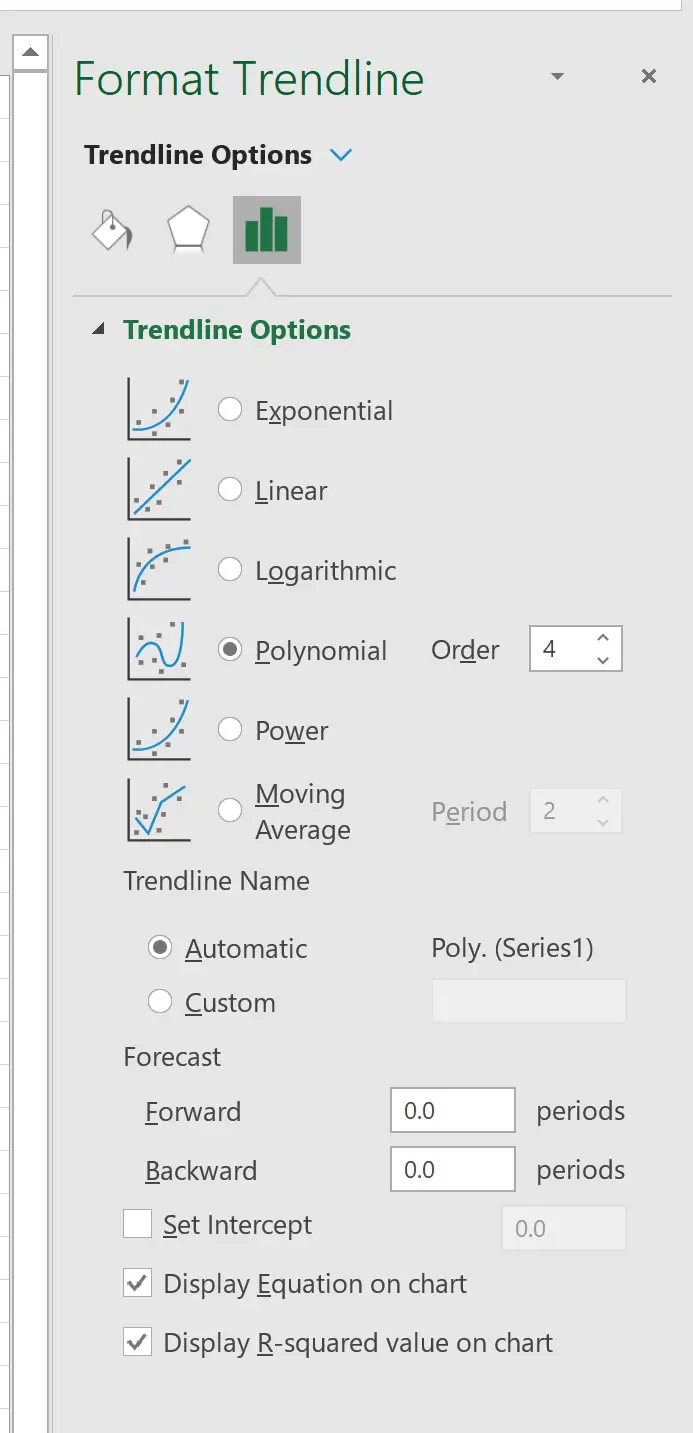
这会产生以下曲线：

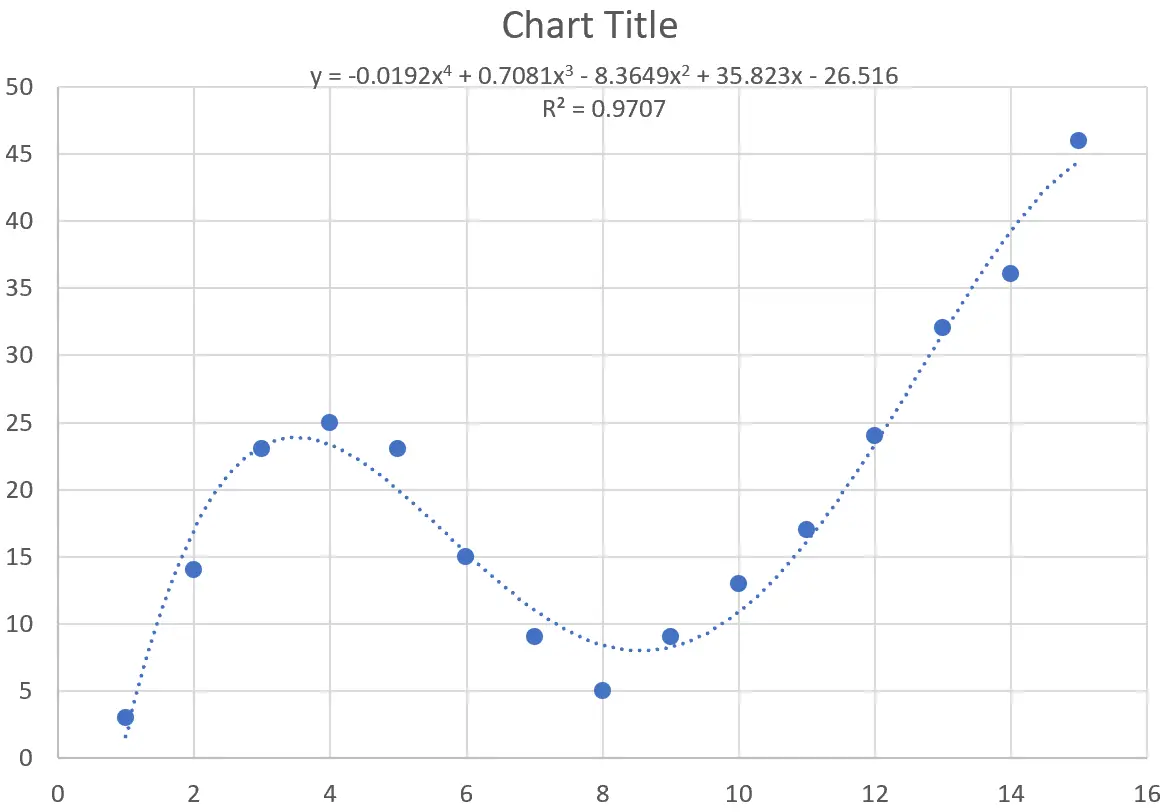
曲线方程如下：

y = -0.0192x ⁴ + 0.7081x ³ – 8.3649x ² + 35.823x – 26.516

该特定曲线的 R 平方为0.9707 。

该 R 平方远高于之前曲线的 R 平方，表明它与数据集的匹配更加紧密。

我们还可以使用该曲线方程根据预测变量来预测响应变量的值。例如，如果x = 4 那么我们将预测y = 23.34 ：

y = -0.0192(4) ⁴ + 0.7081(4) ³ – 8.3649(4) ² + 35.823(4) – 26.516 = 23.34

您可以在此页面上找到更多 Excel 教程。