如何在 excel 中执行不等方差的 t 检验

双样本 t 检验用于确定两个总体的平均值是否相等。

您可以使用两个 t 检验示例的两个版本：

• 等方差 t 检验
• 方差不等的 t 检验

当两个样本的方差不相等时，我们使用方差不等的 t 检验。

确定两个样本之间的方差是否相等的最简单方法是使用方差经验法则。

作为一般规则，如果最大方差与最小方差之比小于 4，我们可以假设方差近似相等。

否则，如果比率等于或大于 4，则假定方差不相等。

以下分步示例演示如何在 Excel 中执行不等方差的双样本 t 检验。

第 1 步：输入数据

假设我们想要确定两种不同的学习方法是否会导致给定大学的学生平均考试成绩不同。

我们随机抽取 20 名学生来使用每种学习方法并记录他们的考试结果：

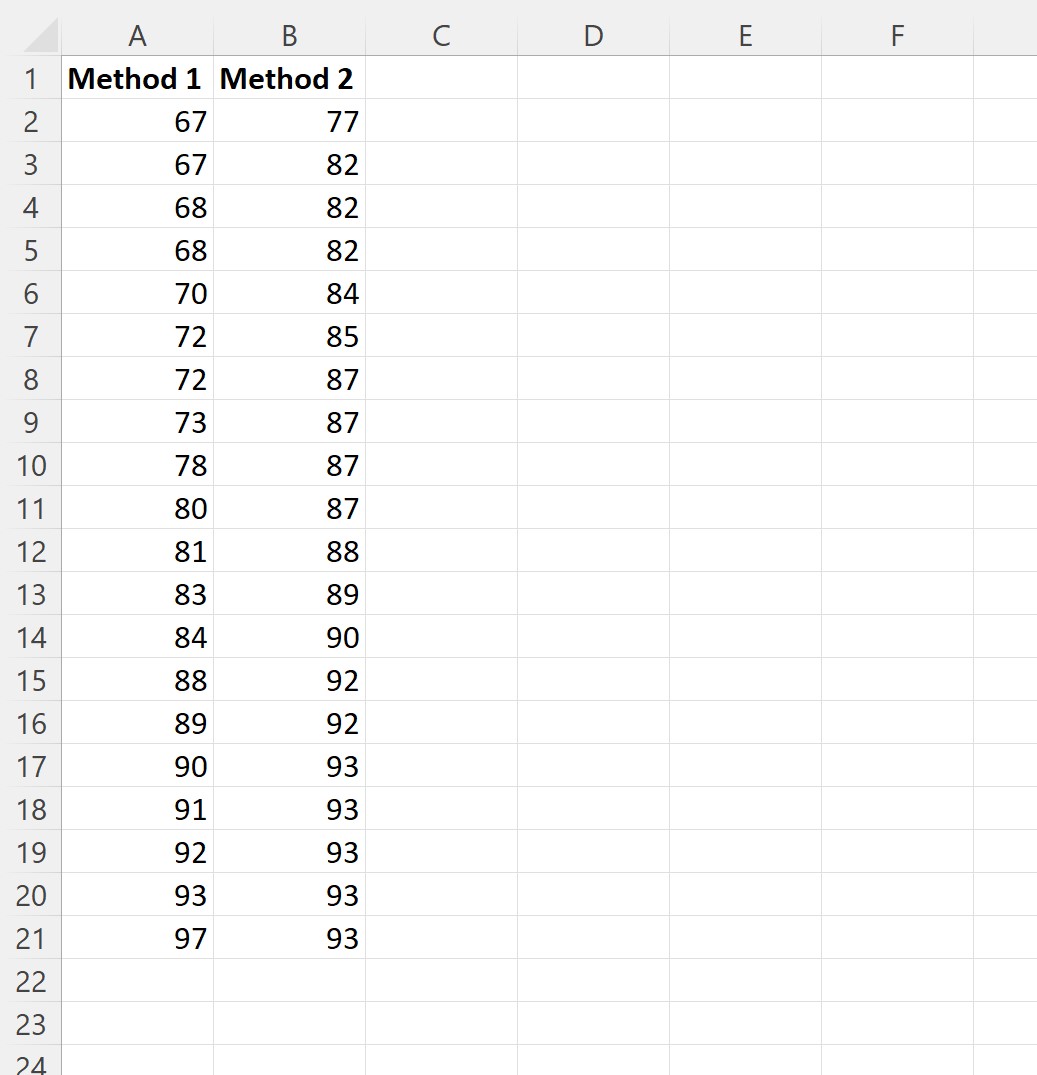
步骤 2：确定相等或不等方差

然后我们可以计算样本方差之比：

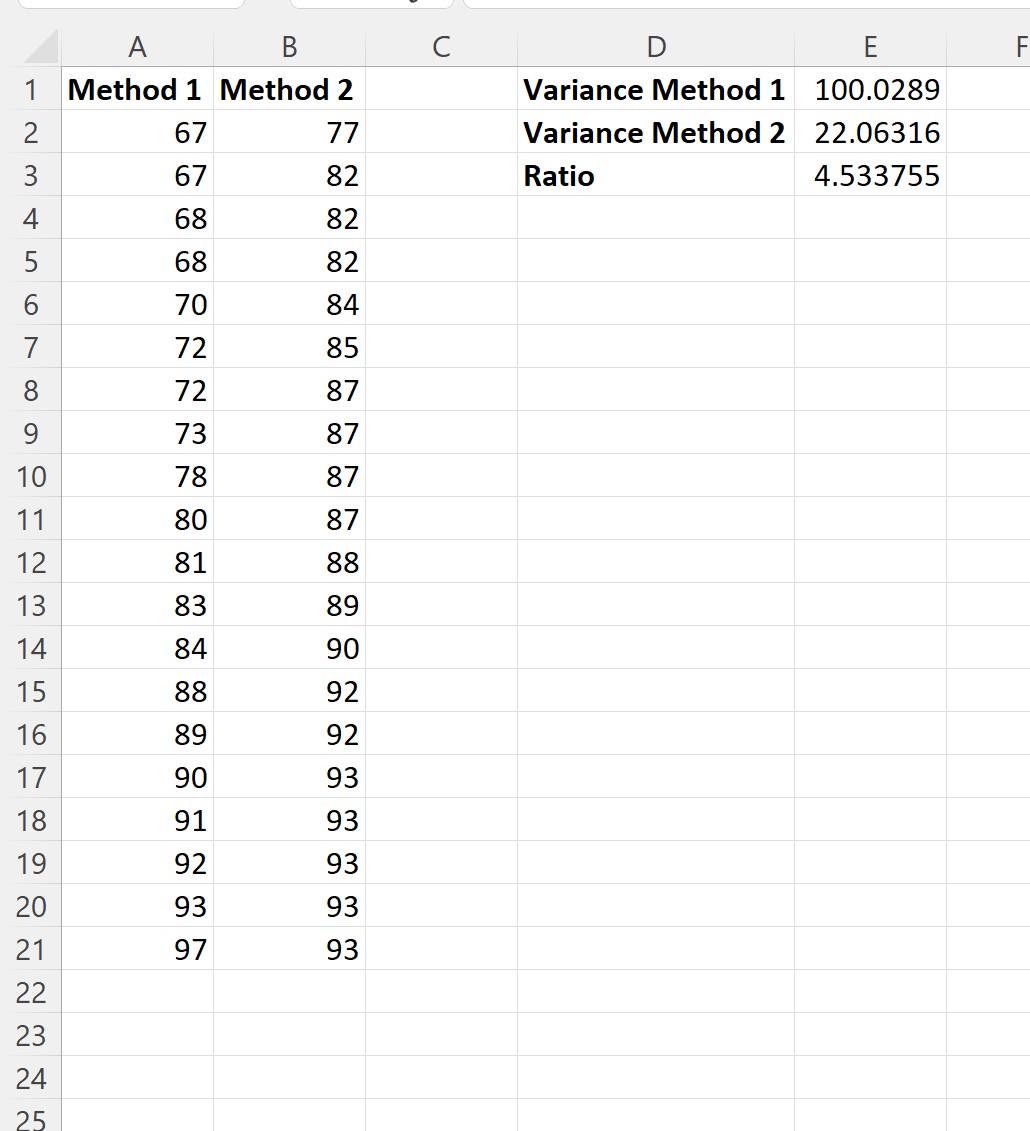
以下是我们在每个单元格中输入的公式：

• 单元格 E1： =VAR.S(A2:A21)
• 单元格 E2： =VAR.S(B2:B21)
• 单元格 E3： =E1/E2

我们可以看到最大样本方差与最小样本方差的比值为4.533755 。

该值大于或等于 4，我们假设两个样本之间的方差不相等。

步骤 3：执行不等方差的双样本 t 检验

接下来，我们可以进行方差不等的双样本 t 检验，以确定两个样本之间的平均考试成绩是否相等。

为此，请单击顶部功能区中的“数据”选项卡，然后单击“分析”组中的“数据分析”按钮：

如果您没有看到此按钮，则首先需要在 Excel 中安装免费的数据分析工具库。

在出现的新窗口中，单击T 检验：假设方差不等的两个样本，然后单击确定：

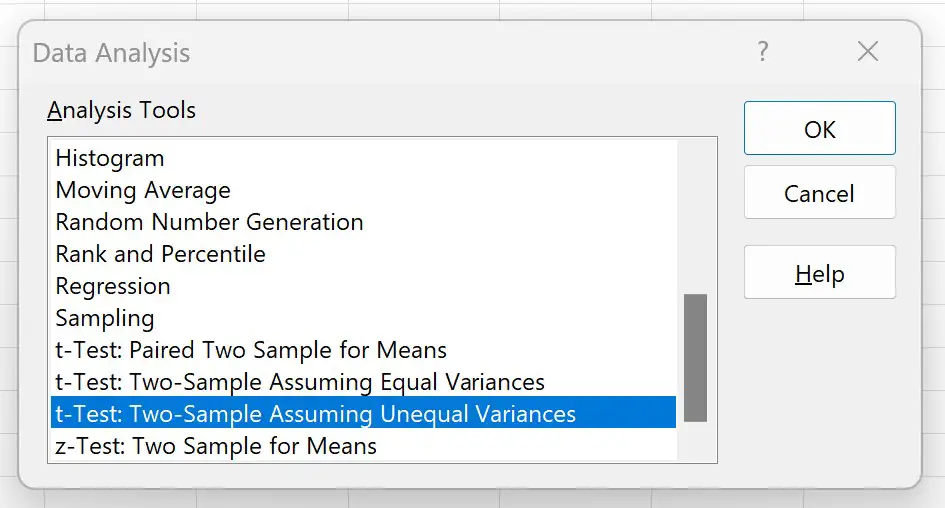
在出现的新窗口中，填写以下信息，然后单击“确定” ：

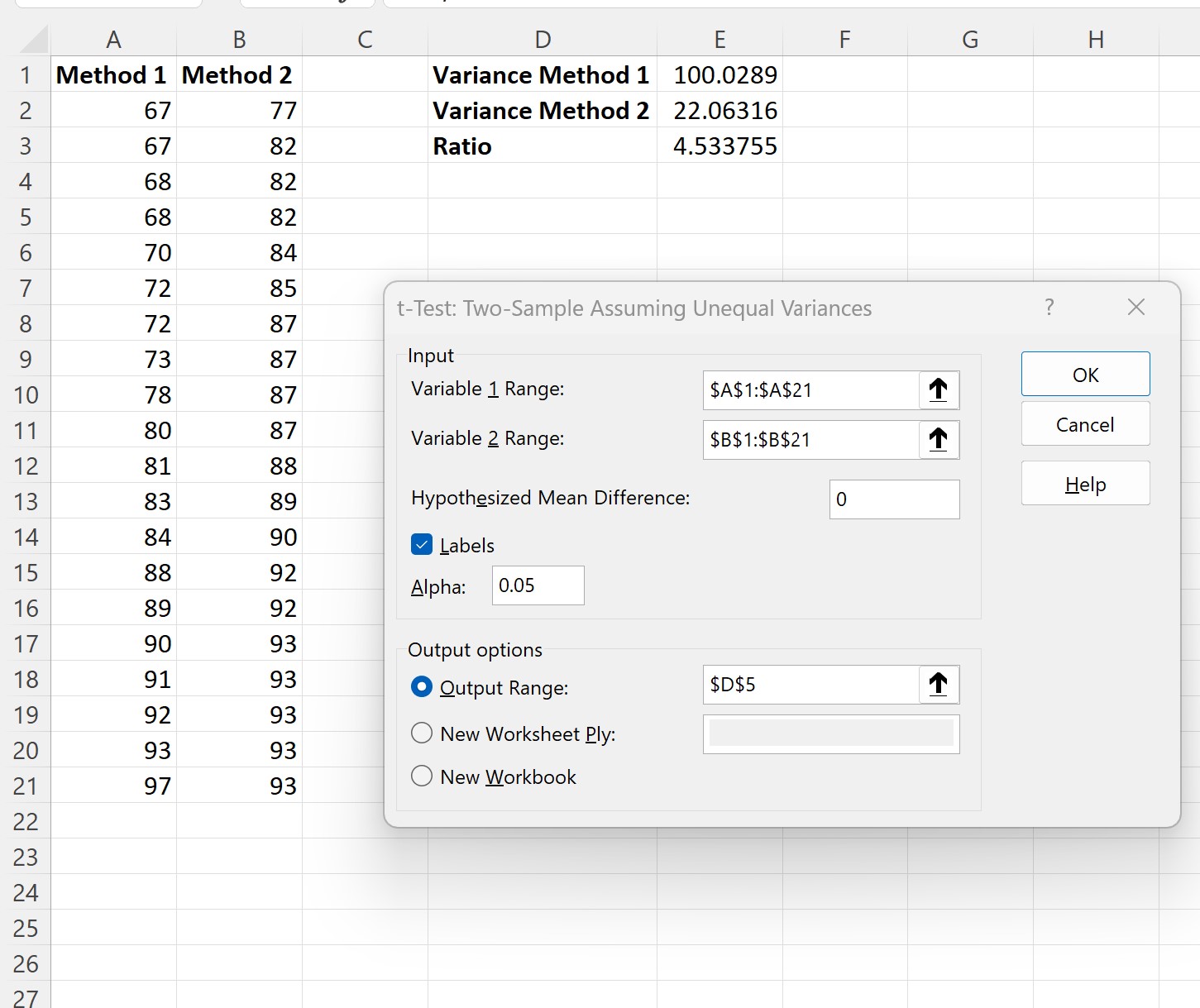
单击“确定”后，将显示两个 t 检验示例的结果：

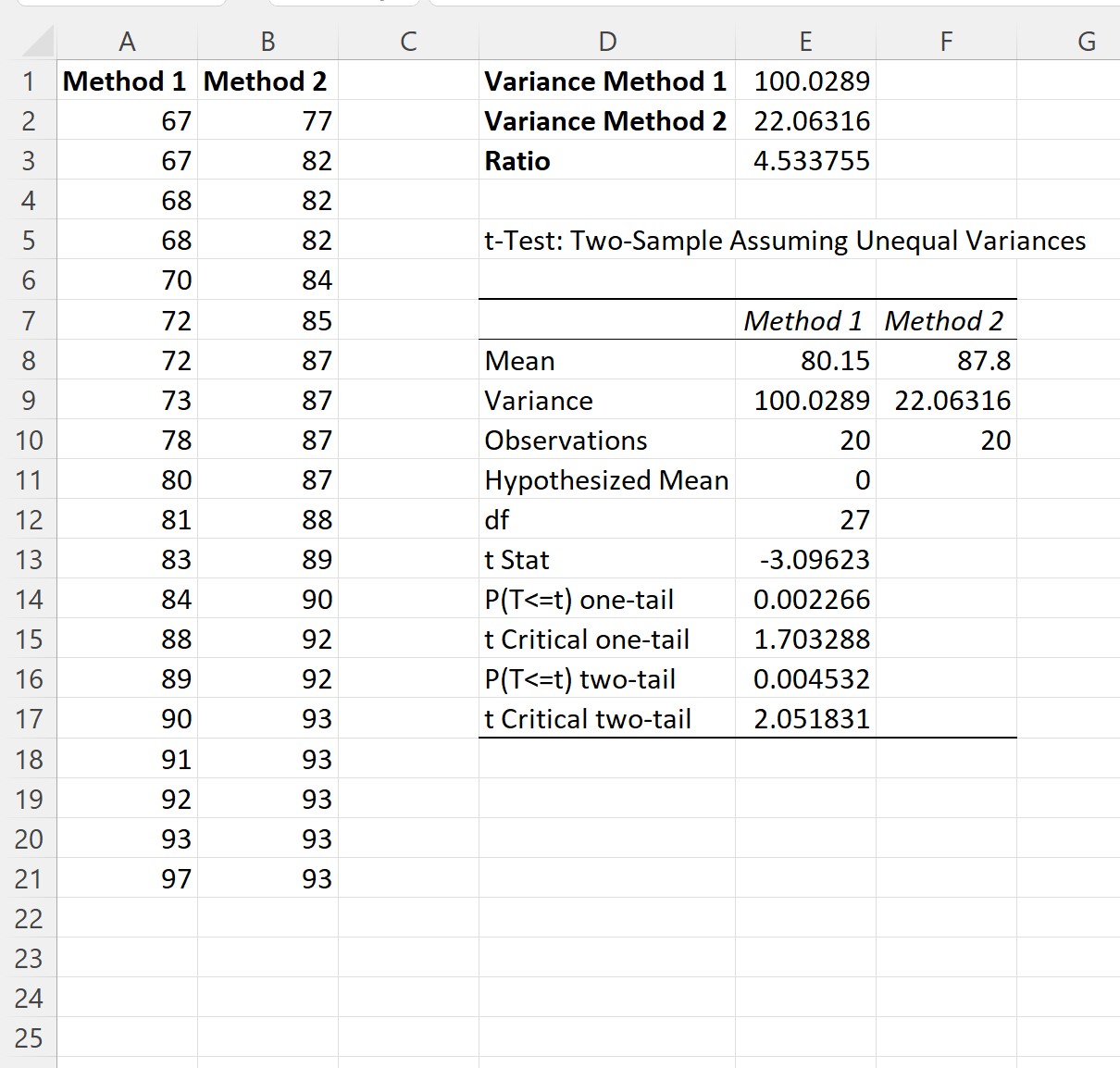
第 4 步：解释结果

从结果我们可以看出：

• 方法 1 的平均考试成绩为80.15 。
• 方法 2 的平均考试成绩为87.8 分。
• t 检验统计量为-3.09623 。
• 相应的双尾 p 值为0.004532 。

由于该 p 值小于 0.05，我们可以得出结论，两种研究方法之间的平均考试成绩存在统计上的显着差异。

其他资源

以下教程说明如何在 Excel 中执行其他常见任务：

如何在 Excel 中执行单样本 t 检验
如何在 Excel 中执行配对样本 t 检验
如何在 Excel 中执行一个样本和两个样本 Z 检验