Excel 中的 stdev.p 与 stdev.s：有什么区别？

您可以使用三种不同的函数来计算 Excel 中的标准差：

1. STDEV.P：该函数计算总体标准差。当值的范围代表整个总体时使用此函数。

该函数使用以下公式：

总体标准差 = √Σ ( _xi – μ) ² / N

金子：

• Σ：希腊符号，意思是“和”
• x _i ：数据集的^{第 i 个}值
• μ：总体平均值
• N：观察总数

2. STDEV.S：该函数计算样本的标准差。当值范围代表值样本而不是整个总体时，请使用此函数。

该函数使用以下公式：

样本标准差 = √Σ ( _xi – x ) ² / (n-1)

金子：

• Σ：希腊符号，意思是“和”
• x _i ：数据集的^{第 i 个}值
• x ：样本平均值
• N：观察总数

3. STDEV：该函数还计算样本标准差。它将返回与STDEV.S函数完全相同的值。

技术说明：

由于总体标准差公式除以N而不是n-1 ，因此总体标准差将始终小于样本标准差。

总体标准差会较小的原因是，如果我们知道每个总体值，那么我们就知道确切的标准差。

然而，当我们只有总体样本时，总体总体的确切标准差有更多的不确定性，因此我们对标准差的估计必须更大。

下面的例子展示了如何在实践中使用这些函数。

示例：Excel 中的 STDEV.P 与 STDEV.S

假设我们在Excel中有以下数据集：

以下屏幕截图显示了如何使用三种不同的标准差公式计算数据集的标准差：

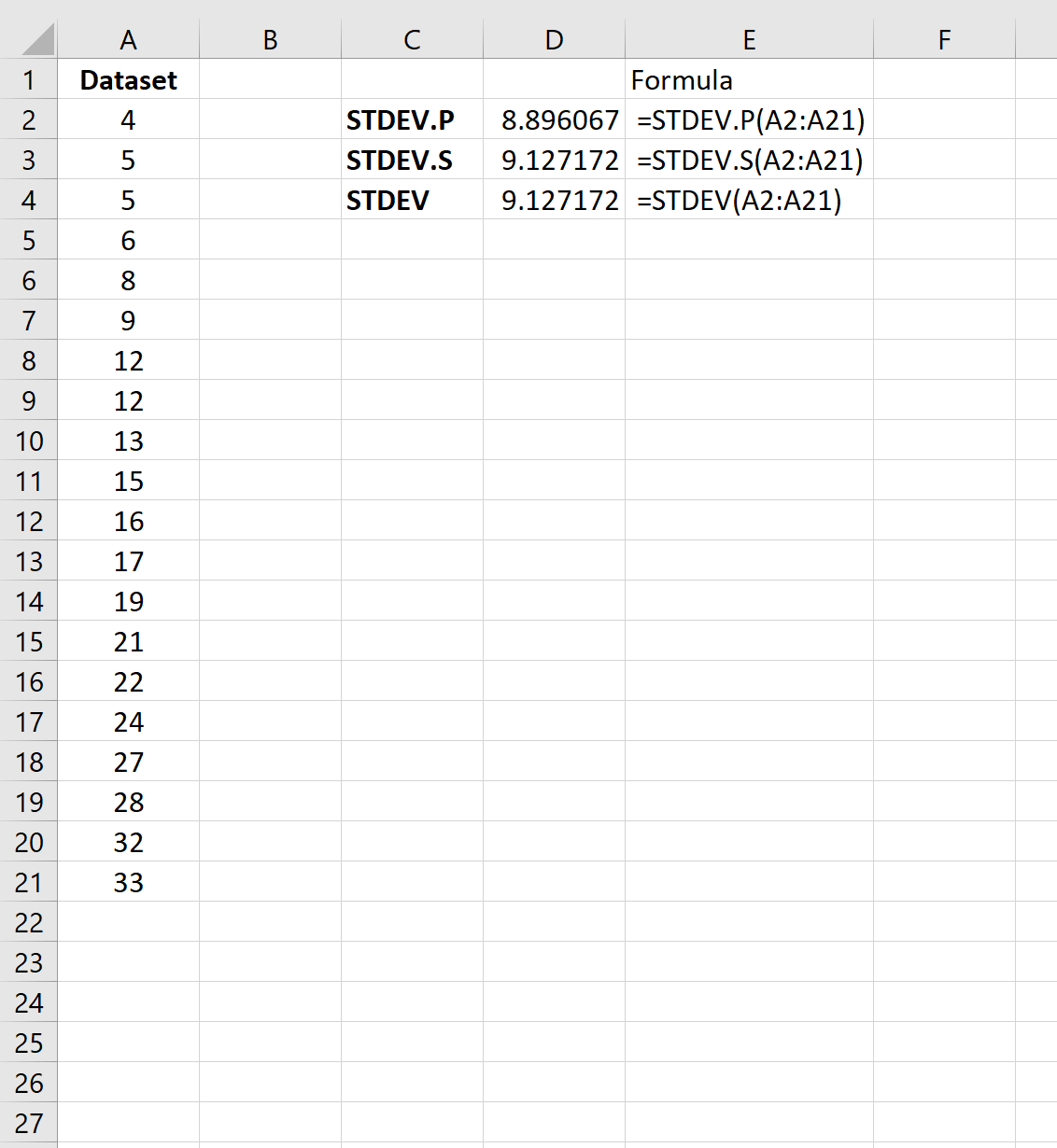
样本标准差为9.127 ，总体标准差为8.896 。

如前所述，总体标准差始终小于样本标准差。

何时使用 STDEV.P 与 STDEV.S

在大多数情况下，我们无法收集整个人群的数据。因此，我们仅收集人口样本的数据。

所以，我们几乎总是使用STDEV.S来计算数据集的标准差，因为我们的数据集通常代表一个样本。

请注意， STDEV和STDEV.S返回完全相同的值，因此我们可以使用任一函数来计算给定数据集的样本标准差。