Excel：计算回归系数的置信区间

在线性回归模型中，回归系数告诉我们与预测变量增加一个单位相关的响应变量的平均变化。

我们可以使用以下公式来计算回归系数的置信区间：

β ₁的置信区间：b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

金子：

•   b ₁ = 回归表中显示的回归系数
• t _{1-∝/2, n-2} = 具有 n-2 自由度的 1-∝ 置信水平的临界 t 值，其中n是数据集中的观测总数
• se(b ₁ ) = 回归表中显示的 b ₁标准误差

以下示例演示如何在 Excel 中计算回归系数的置信区间。

示例：Excel 中回归系数的置信区间

假设我们想要拟合一个简单的线性回归模型，使用学习时间作为预测变量，考试成绩作为特定班级 15 名学生的响应变量：

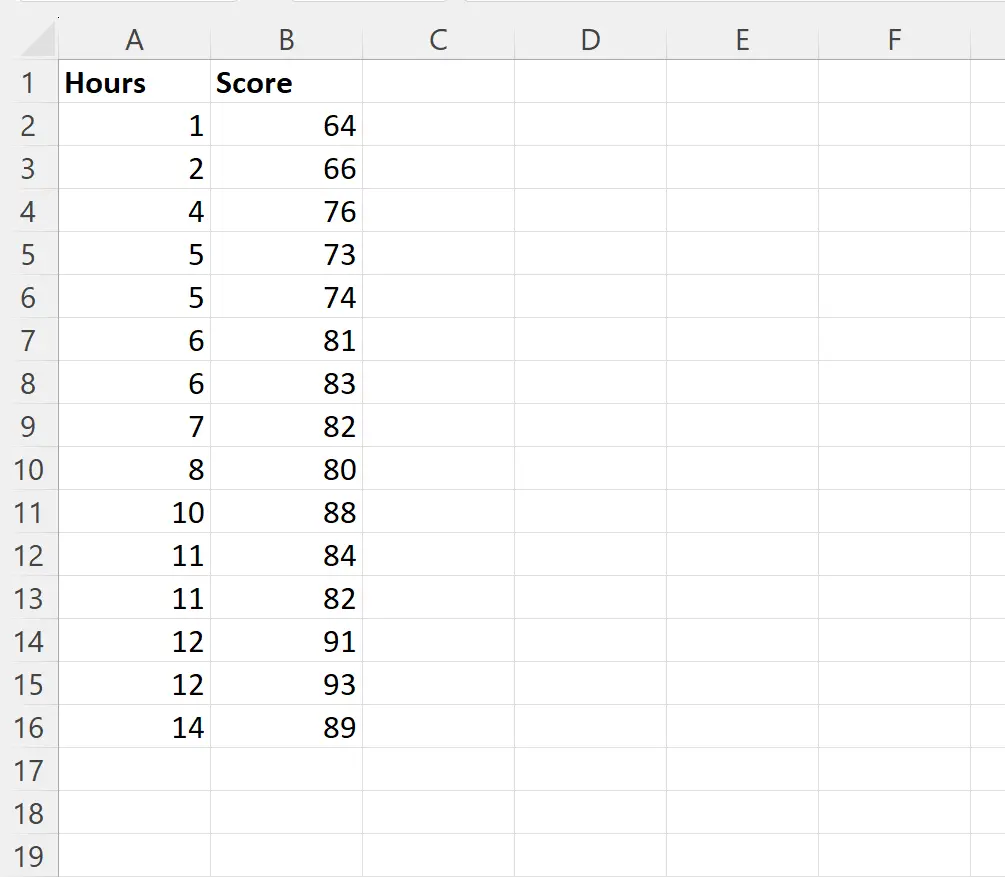
我们可以在单元格 D2 中键入以下公式，使用“小时”列中的值作为预测变量、 “分数”列中的值作为响应变量来执行简单线性回归：

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

请注意，第一个TRUE参数告诉 Excel 通常计算回归方程的截距，而不强制其为零。

第二个TRUE参数告诉 Excel 除了系数之外还生成其他回归统计数据。

下面的屏幕截图显示了该公式的结果（我们在输出下方的红色文本中解释了每个输出值代表的含义）：

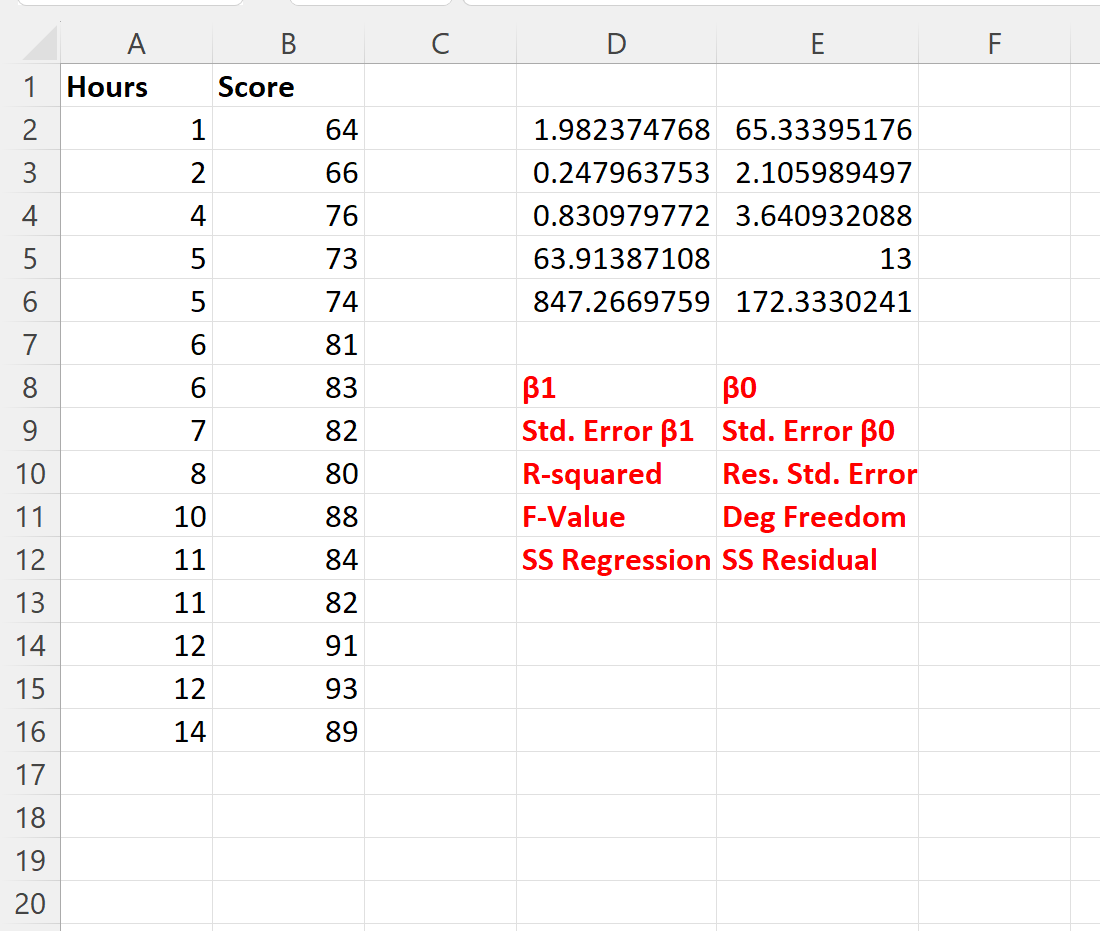
利用回归系数，我们可以写出拟合回归方程如下：

分数 = 65.334 + 1.982*（学习时间）

请注意，小时数的回归系数为1.982 。

这告诉我们，每多花一小时的学习时间，考试成绩就会平均提高1,982分。

要计算回归系数的 95% 置信区间，我们可以在单元格 H2 和 H3 中输入以下公式：

• H2: = D2 – T.INV.2T(0.05, E5)*D3
• H3: = D2 + T.INV.2T(0.05, E5)*D3

以下屏幕截图显示了如何在实践中使用这些公式：

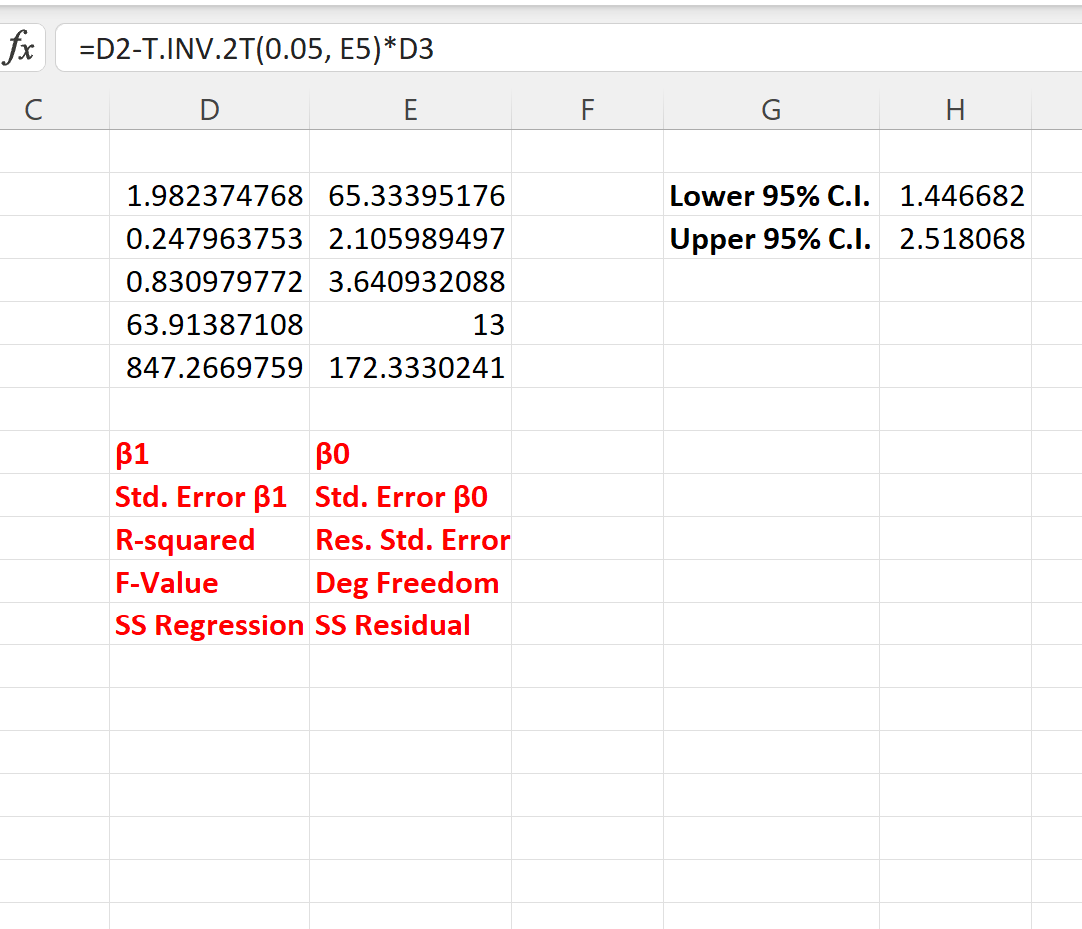
回归系数的 95% 置信区间为[1.446, 2.518] 。

由于此置信区间不包含值 0 ，我们可以得出结论，学习时间和考试成绩之间存在统计上显着的关联。

我们还可以通过手动计算回归系数的 95% 置信区间来确认这是正确的：

• β ₁的 95% CI：b ₁ ± t _1-α/2，n-2 * se(b ₁ )
• β ₁的 95% CI：1.982 ± t _{0.975, 15-2} * 0.248
• β ₁的 95% CI：1.982 ± 2.1604 * 0.248
• β ₁的 95% CI：[1.446, 2.518]

回归系数的 95% 置信区间为[1.446, 2.518] 。

其他资源

以下教程说明如何在 Excel 中执行其他常见任务：

如何在 Excel 中执行简单线性回归
如何在 Excel 中执行多元线性回归
如何在Excel中解释回归输出中的P值