如何在 excel 中计算抽样分布
抽样分布是基于来自单个总体的许多随机样本的特定统计量的概率分布。
本教程介绍如何在 Excel 中对抽样分布执行以下操作:
- 生成抽样分布。
- 可视化样本分布。
- 计算抽样分布的平均值和标准差。
- 计算有关抽样分布的概率。
在 Excel 中生成抽样分布
假设我们要生成一个由1,000 个样本组成的抽样分布,其中每个样本大小为20 ,并且来自均值为5.3和标准差为9的正态分布。
我们可以通过在电子表格的单元格 A2 中输入以下公式来轻松完成此操作:
= NORM . INV ( RAND (), 5.3, 9)
然后,我们可以将鼠标悬停在单元格的右下角,直到出现一个小+ ,然后将公式拖动到右侧 20 个单元格和向下 1000 个单元格:
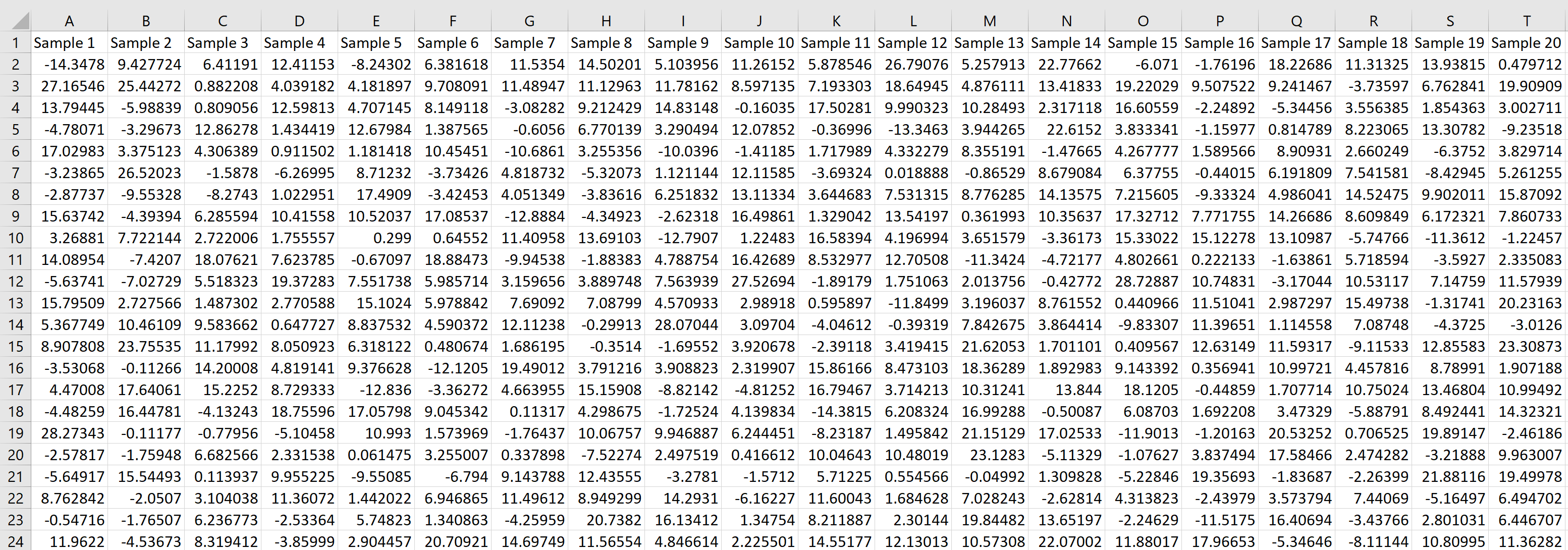
每行代表大小为 20 的样本,其中每个值均来自平均值为 5.3、标准差为 9 的正态分布。
求平均值和标准差
为了找到样本均值的抽样分布的均值和标准差,我们可以首先通过在工作表的单元格 U2 中输入以下公式来找到每个样本的均值:
= AVERAGE (A2:T2)
然后,我们可以将鼠标悬停在单元格的右下角,直到出现一个小+ ,然后双击将此公式复制到 U 列中的所有其他单元格:
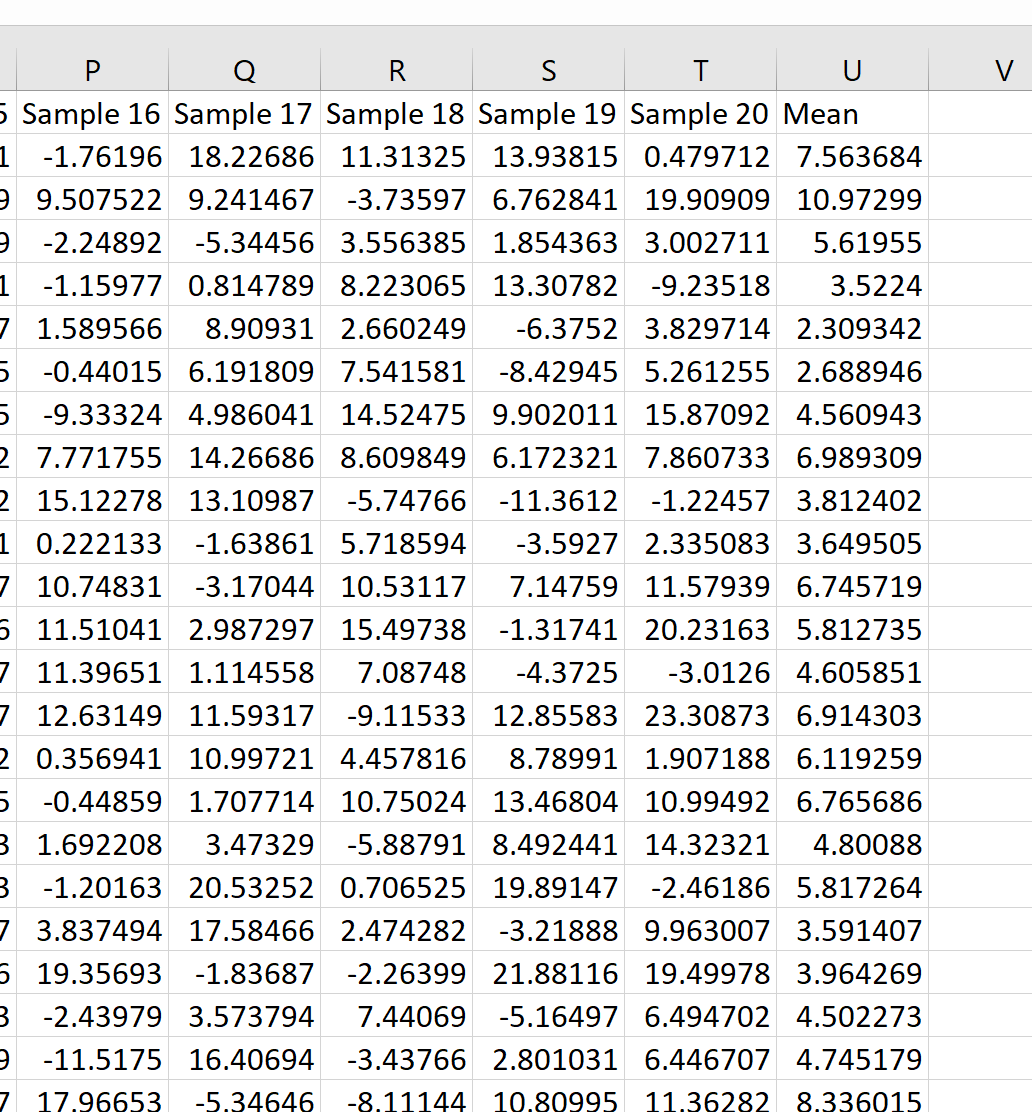
我们可以看到第一个样本的平均值为 7.563684,第二个样本的平均值为 10.97299,依此类推。
然后我们可以使用以下公式来计算样本均值的均值和标准差:
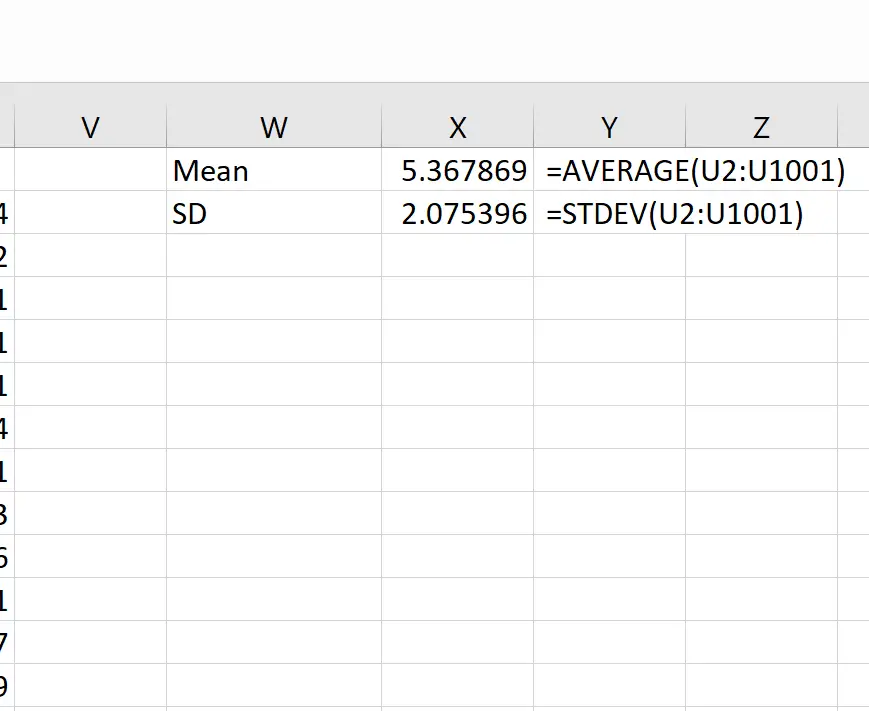
理论上,抽样分布的均值应为 5.3。我们可以看到,本例中的实际样本均值是5.367869 ,接近 5.3。
理论上,抽样分布的标准差应该等于 s/√n,即 9 / √20 = 2.012。我们可以看到,抽样分布的实际标准差是2.075396 ,接近 2.012。
可视化样本分布
我们还可以创建一个简单的直方图来可视化样本均值的采样分布。
为此,只需突出显示 U 列中的所有样本均值,单击“插入”选项卡,然后单击“图表”部分下的“直方图”选项。
这给出了以下直方图:
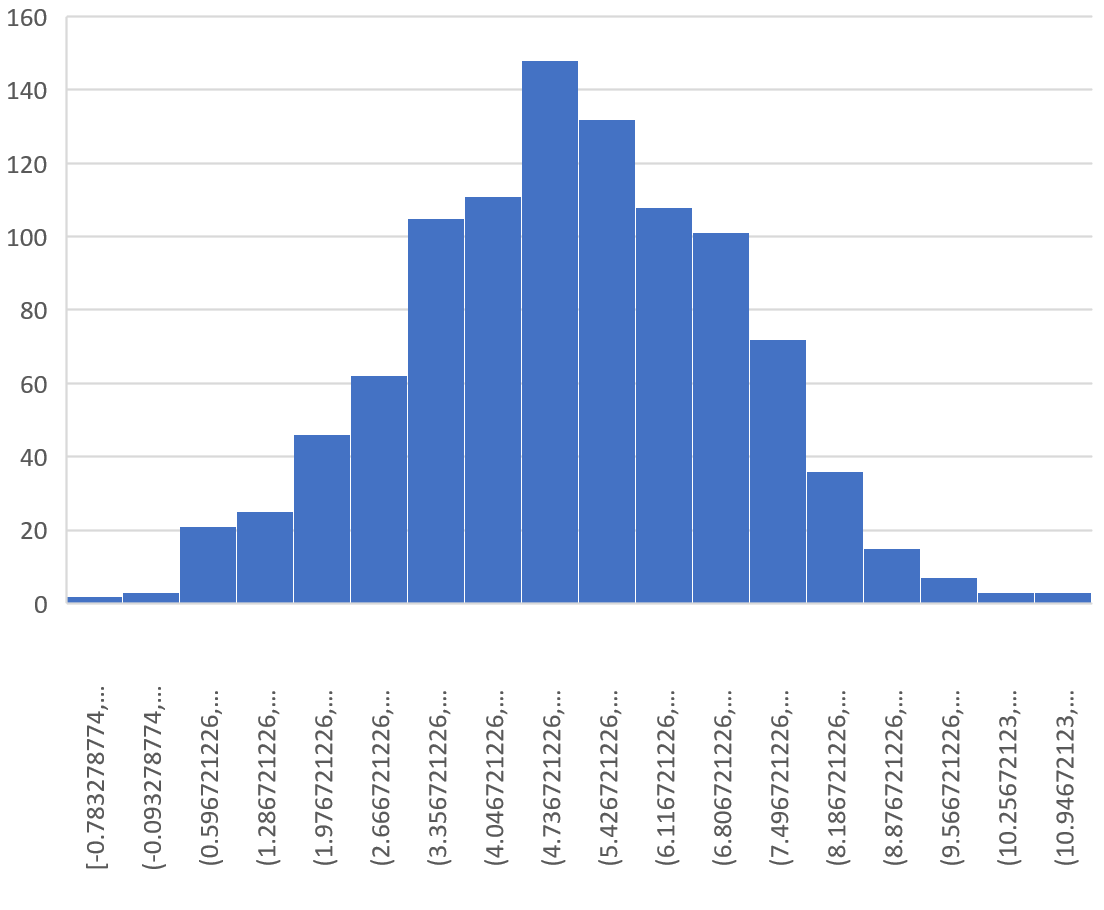
可以看出,采样分布呈钟形,峰值位于值 5 附近。
然而,从分布的尾部我们可以看到,一些样本的均值大于 10,而另一些样本的均值小于 0。
计算概率
我们还可以根据总体均值、总体标准差和样本量来计算样本均值获得特定值的概率。
例如,假设总体平均值为 5.3、总体标准差为 9、样本量为:,我们可以使用以下公式求出样本平均值小于或等于 6 的概率:
= COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)
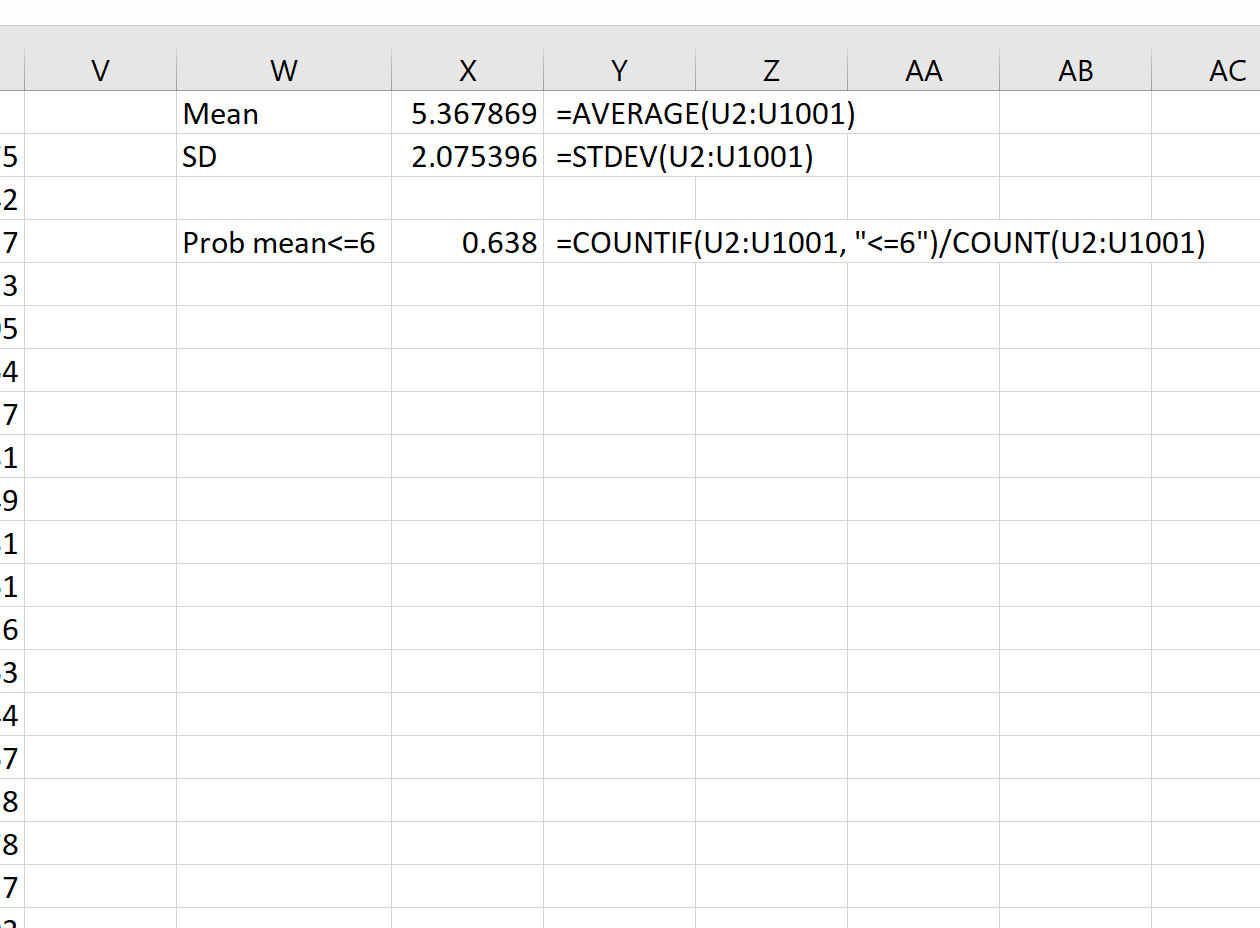
我们看到样本均值小于或等于 6 的概率为0.638。
这与采样分布计算器计算的概率非常接近:
