如何在 excel 中计算回归的标准误差

我们拟合一个线性回归模型，模型采用以下形式：

Y = β ₀ + β ₁ X + … + β _i

其中 ϵ 是独立于 X 的误差项。

无论如何使用X来预测Y的值，模型中总会存在随机误差。

测量这种随机误差的分散性的一种方法是使用回归模型的标准误差，这是一种测量残差ϵ 标准差的方法。

本教程提供了如何在 Excel 中计算回归模型的标准误差的分步示例。

第 1 步：创建数据

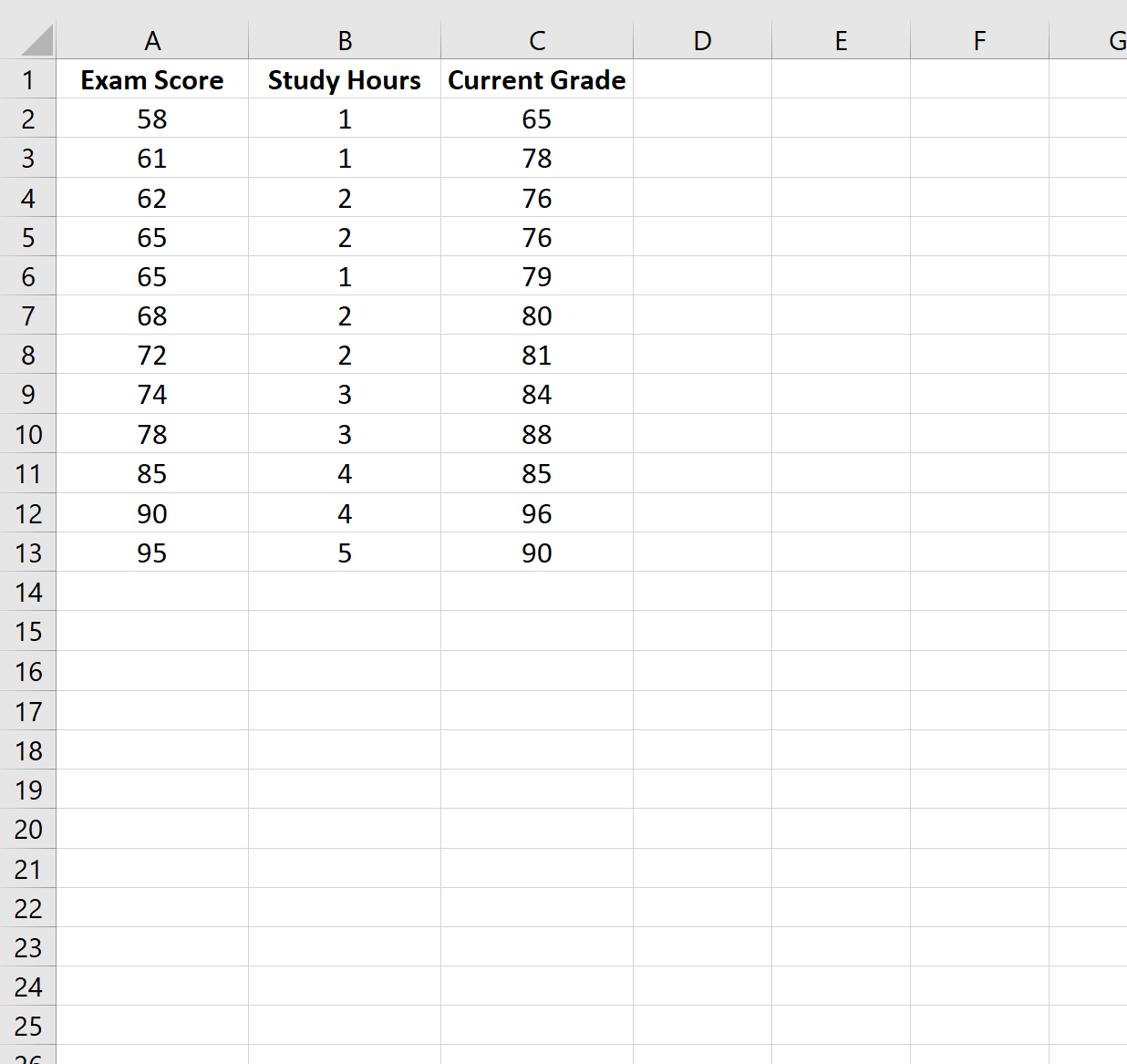
在此示例中，我们将为 12 名不同的学生创建一个包含以下变量的数据集：

• 考试成绩
• 学习时间
• 当前班级

步骤 2：拟合回归模型

接下来，我们将使用考试成绩作为响应变量、学习时间和当前成绩作为预测变量来拟合多元线性回归模型。

为此，请单击顶部功能区的“数据”选项卡，然后单击“数据分析” ：

如果此选项不可用，您必须首先加载数据分析工具库。

在出现的窗口中，选择回归。在出现的新窗口中，提供以下信息：

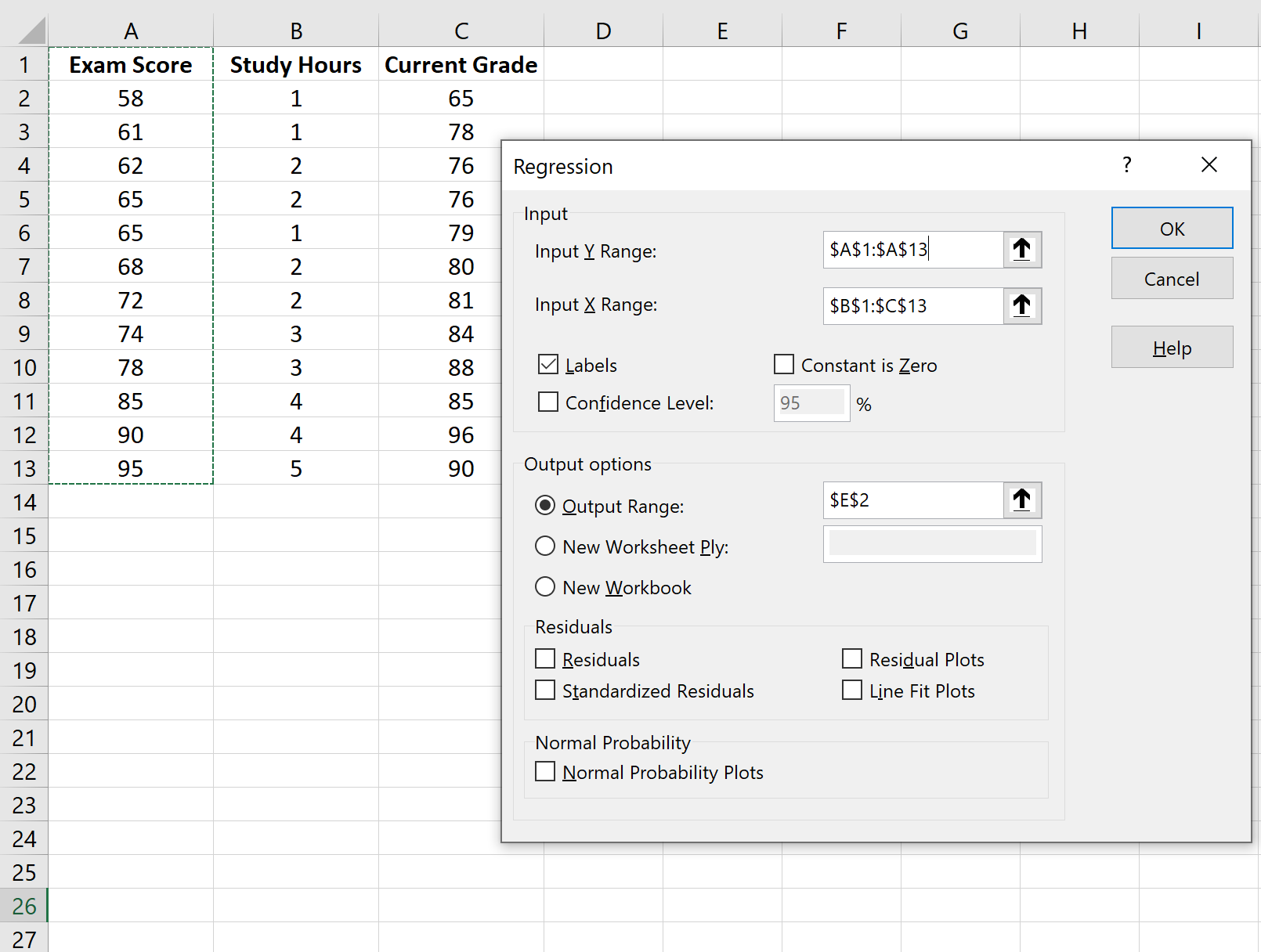
单击“确定”后，将出现回归模型输出：

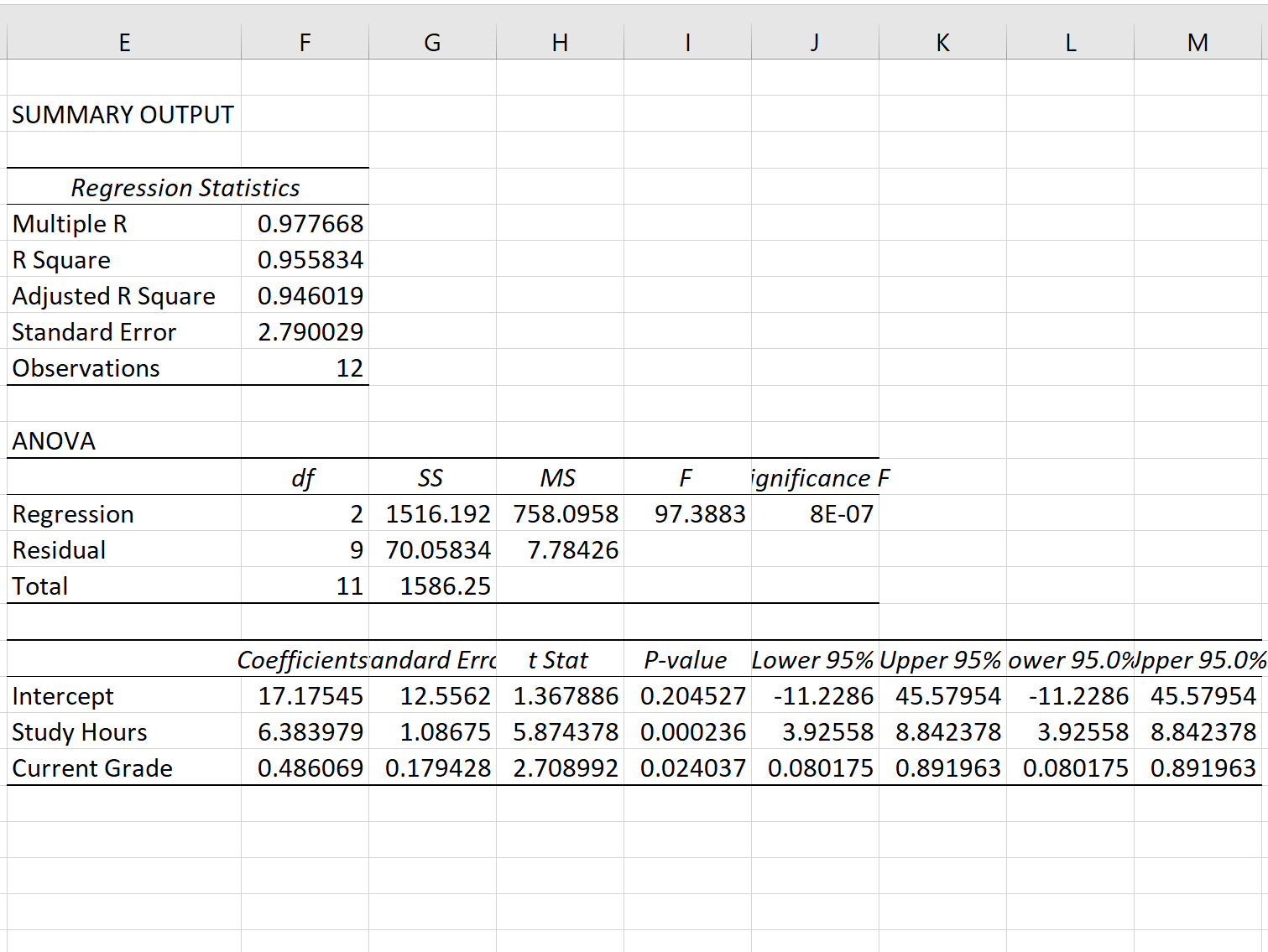
步骤 3：解释回归标准误差

回归模型的标准误差是标准误差旁边的数字：

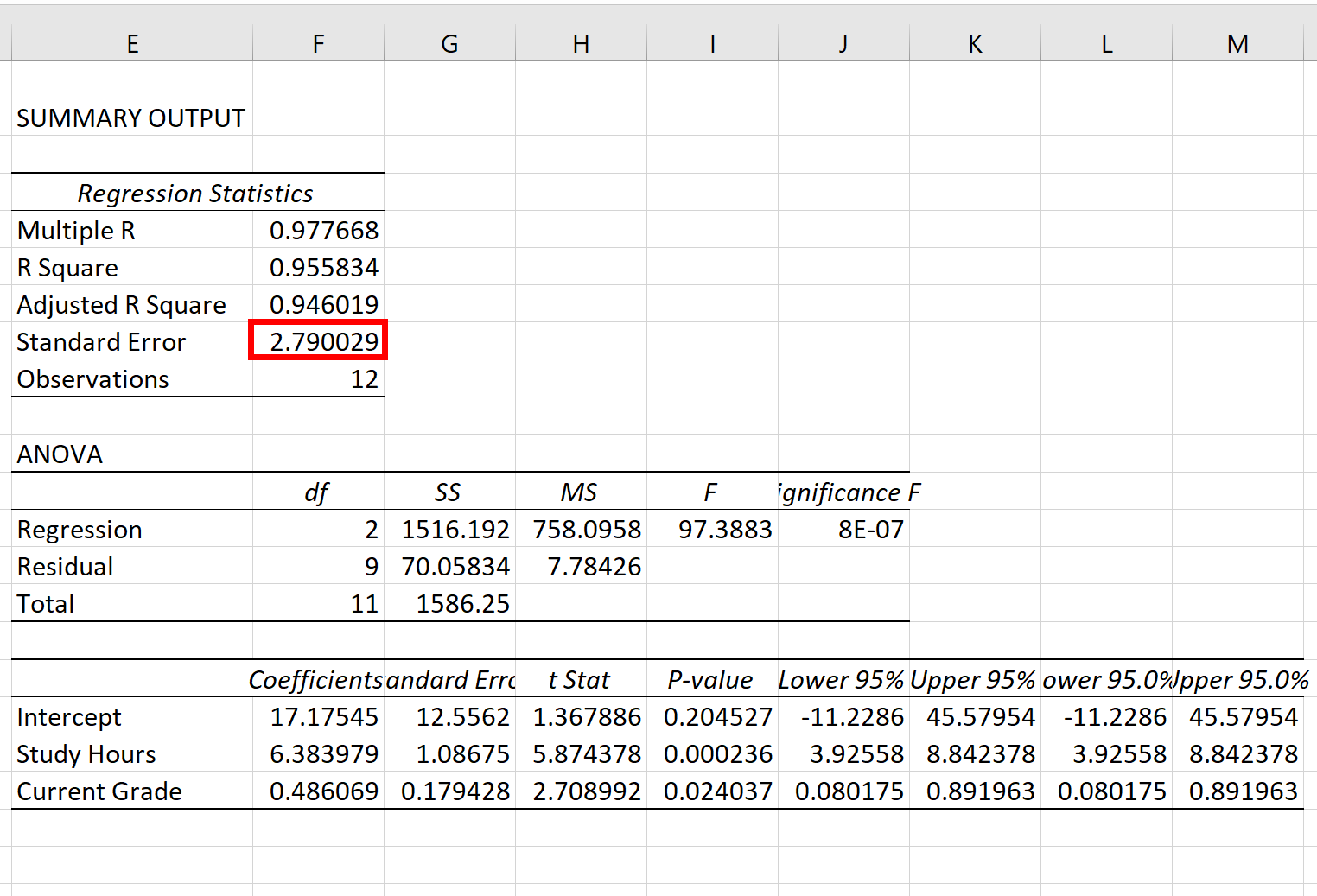
该特定回归模型的标准误差为2.790029 。

该数字表示实际考试结果与模型预测的考试结果之间的平均距离。

请注意，某些考试结果与预测分数相差超过 2.79 个单位，而其他考试结果则更接近。但是，平均而言，实际考试结果与预测结果之间的距离为2.790029 。

另请注意，回归的标准误差越小表明回归模型更适合数据集。

因此，如果我们将新的回归模型拟合到数据集并获得标准误差（例如4.53） ，则该新模型在预测考试分数方面的效果将不如以前的模型。

其他资源

衡量回归模型准确性的另一种常见方法是使用 R 平方。请查看这篇文章，了解使用回归标准误差相对于 R 平方来衡量准确性的好处。