如何在 excel 中绘制方差分析结果图表
单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。
在解释单向方差分析的结果时，创建一个图表来可视化组均值之间的差异会很有帮助。
以下示例演示如何执行单向方差分析并在 Excel 中绘制结果图表。
示例：如何在 Excel 中绘制方差分析结果图表
假设一位教授随机要求班上 30 名学生使用三种学习方法中的一种来准备考试。
以下屏幕截图显示了学生根据他们使用的方法获得的分数：
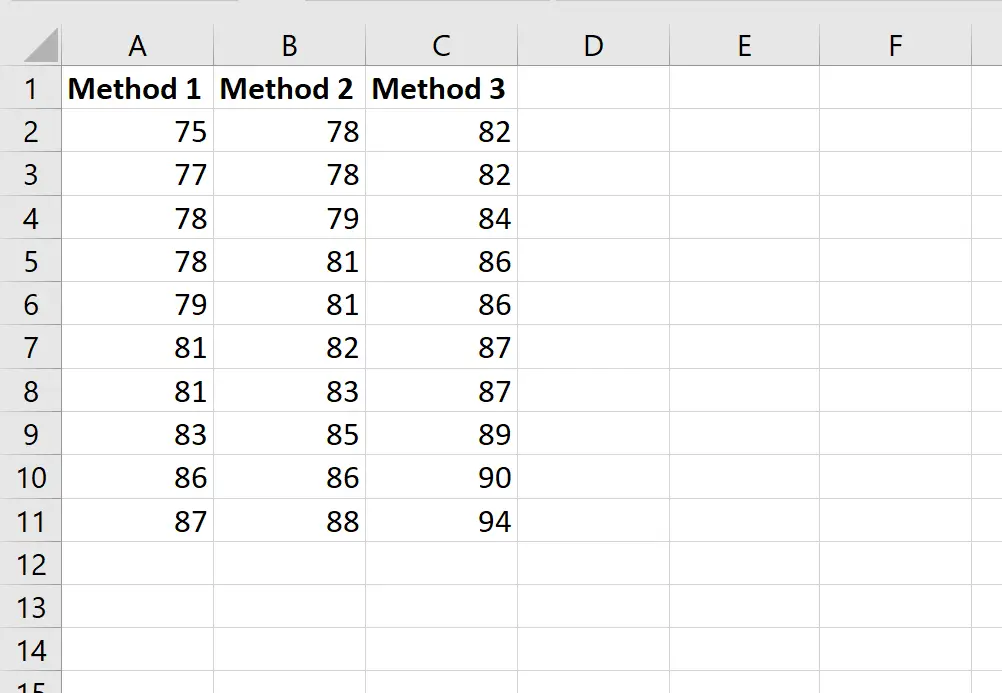
假设教授想要执行单向方差分析以确定三组的平均分数是否相同。
要在 Excel 中执行单向方差分析，请单击顶部功能区的“数据”选项卡，然后单击“分析”组中的“数据分析” 。
如果您没有看到“数据分析”选项，则必须首先加载免费的分析工具库软件。
在出现的新面板中，单击方差分析：单因素，然后单击确定。
在出现的新窗口中，输入以下信息：
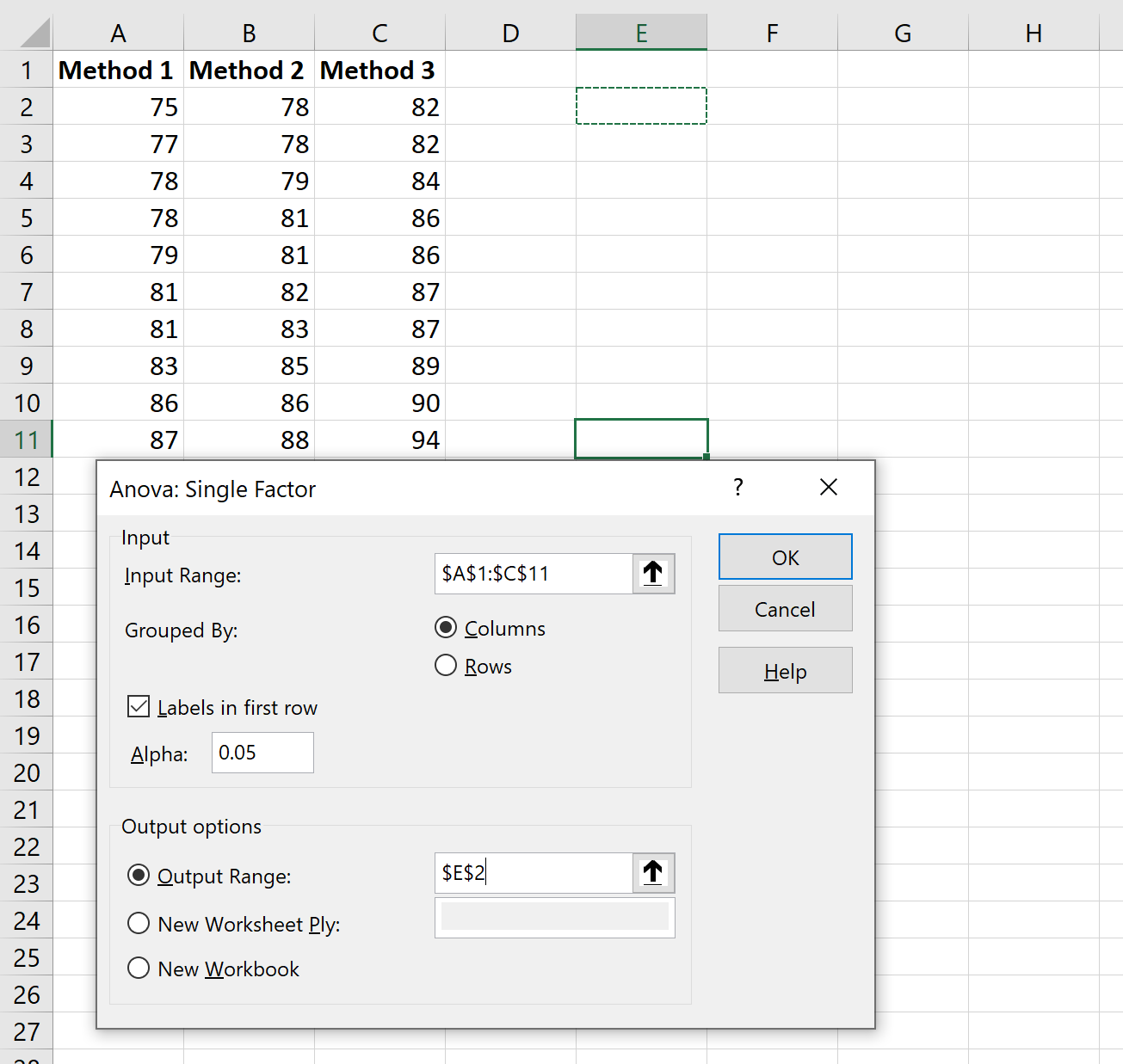
单击“确定”后，将显示单向方差分析结果：
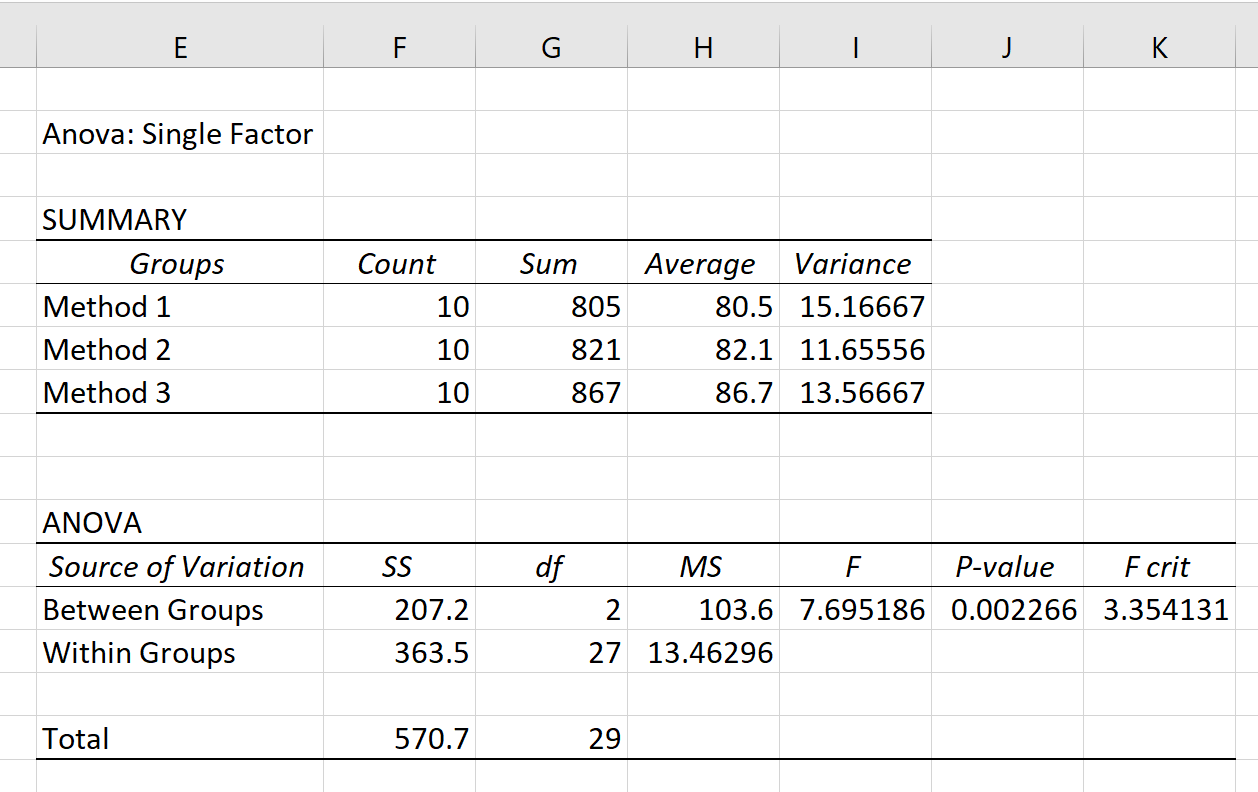
输出中的最大值是p 值，结果为0.002266 。
回想一下，单向方差分析使用以下原假设和备择假设：
- H 0 ：所有组平均值相等。
- H A ：并非所有组的平均值都相同。
由于 p 值小于 α = 0.05，我们拒绝原假设并得出结论：所有组均值不相等。
这意味着并非所有三种学习方法都会产生相同的平均考试成绩。
为了可视化这些方差分析结果，我们可以创建分组箱线图，显示每种研究方法的考试结果分布。
为此，请突出显示单元格区域A2:C11 ，然后单击顶部功能区的“插入”选项卡，然后单击“图表”组中的“方框和须线”图标：
将出现下表：
请随意更改 Y 轴范围并添加图例以使该图表更易于阅读：
每个箱线图显示每种研究方法的检查结果的分布。
每个箱线图中间的线代表每种学习方法的考试分数中位数，小“x”代表平均考试分数。
即使不查看方差分析表的结果，我们也可以看到学习方法 3 的平均考试成绩明显高于其他两种研究方法。
我们还可以看出为什么方差分析表中的 p 值具有统计显着性：三种研究方法显然没有相同的平均值。
通过创建这三个箱线图，我们能够更好地理解单向方差分析的结果。
其他资源
以下教程介绍了如何在 Excel 中执行其他常见操作：
如何在 Excel 中执行单向方差分析
如何在 Excel 中执行双向方差分析
如何在 Excel 中执行重复测量方差分析
如何在 Excel 中执行 Tukey-Kramer 事后检验
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多