如何在 excel 中执行 scheffe 测试

单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。

如果方差分析表的总体p 值低于一定的显着性水平，则我们有足够的证据表明至少其中一个组均值与其他均值不同。

然而，这并没有告诉我们哪些群体彼此不同。这只是告诉我们并非所有组的平均值都是相等的。

为了准确地知道哪些组彼此不同，我们需要执行事后测试来控制每个族的错误率。

最常用的事后检验之一是 Scheffe 检验。

以下分步示例展示了如何在 Excel 中执行 Scheffe 测试。

第 1 步：输入数据

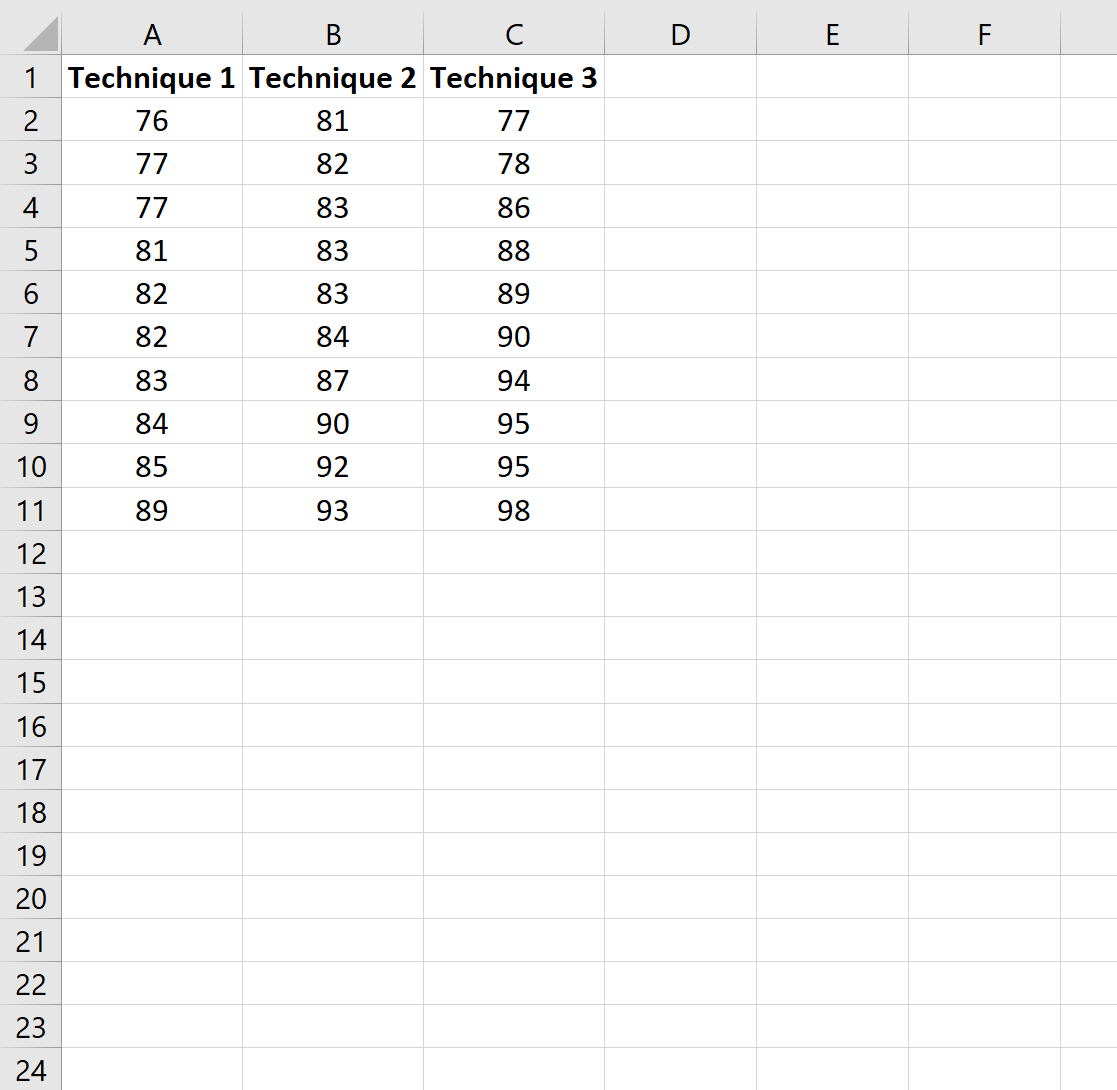
假设老师想知道三种不同的学习技巧是否会导致学生的考试成绩不同。为了测试这一点，她随机分配 10 名学生使用每种学习技巧并记录他们的考试结果。

首先，我们将根据所使用的学习方法输入每个学生的成绩：

第 2 步：执行单向方差分析

要执行单向方差分析，请单击顶部功能区的“数据”选项卡，然后单击“分析”组中的“数据分析”选项。

如果您没有看到此选项，则必须首先加载分析工具库。

在出现的新窗口中，单击方差分析：单因素，然后单击确定。

在出现的新窗口中，提供以下信息：

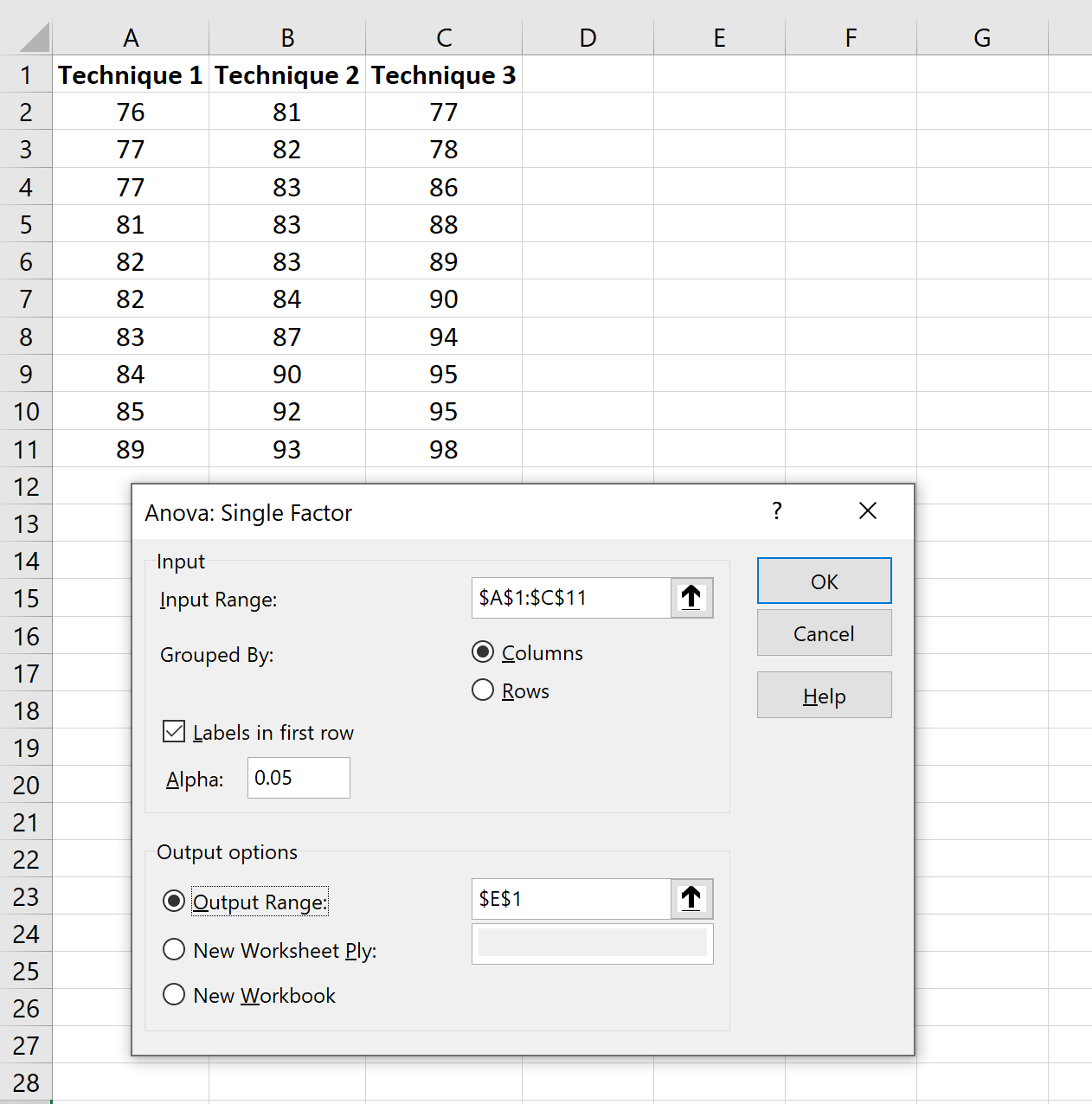
单击“确定”后，将显示单向方差分析结果：

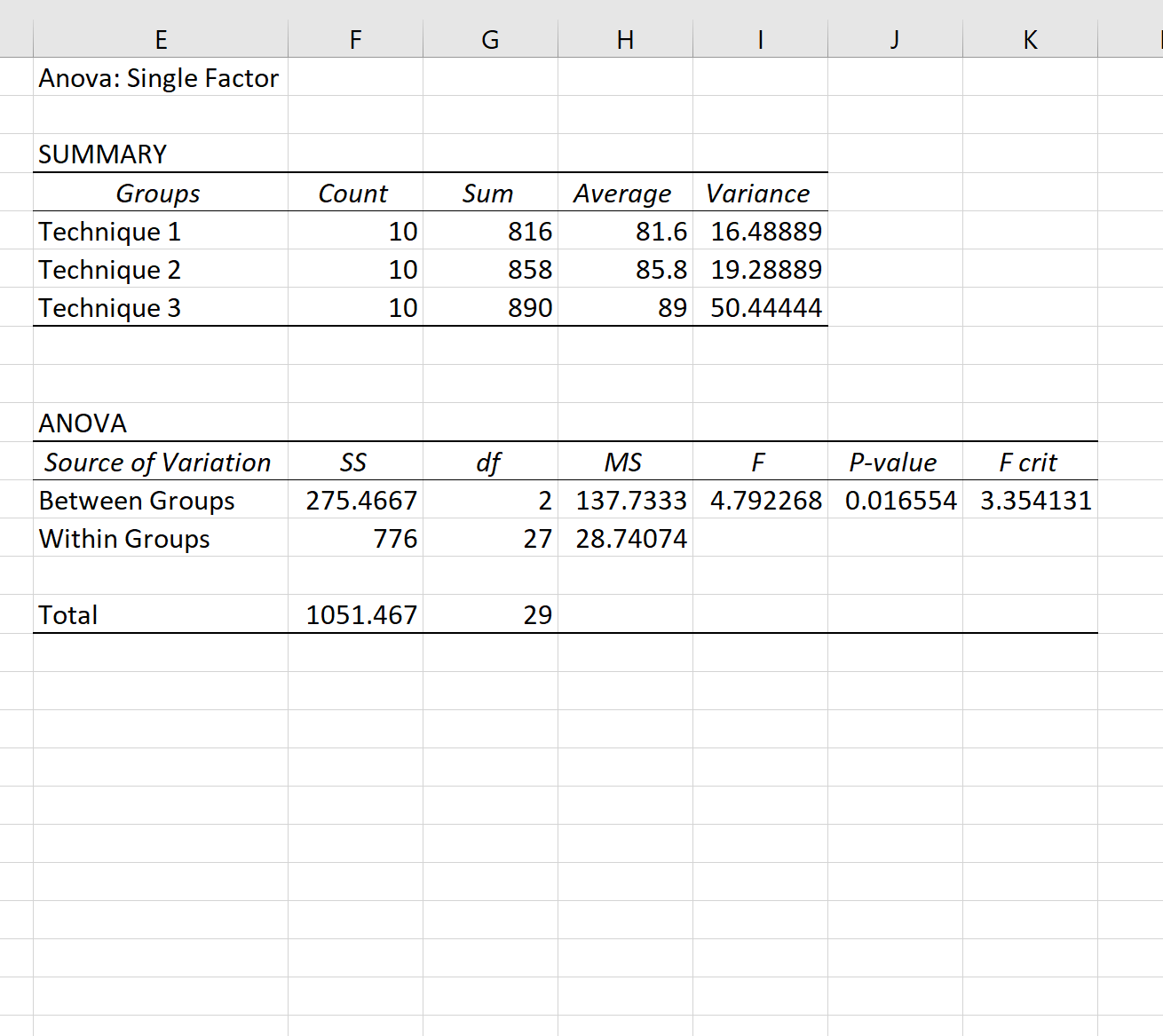
由于方差分析表中的总体 p 值 ( 0.016554 ) 小于 0.05，这意味着每个组的平均考试成绩不同。

接下来，我们将执行 Scheffe 测试来确定哪些组是不同的。

第 3 步：执行 Scheffe 测试

首先，我们需要计算 Scheffe 临界值。计算如下：

Scheffe临界值=F临界值*2

在我们的示例中，Scheffe 临界值为 3.354131 * 2 = 6.708 。

然后我们可以计算每次两两比较的F统计量，计算如下：

F 统计量：( x ₁ – x ₂ ) ² / ((1/n ₁ + 1/n ₂ )_中的MS)

例如，我们可以使用以下公式来计算每种技术之间的成对差异的 F 统计量：

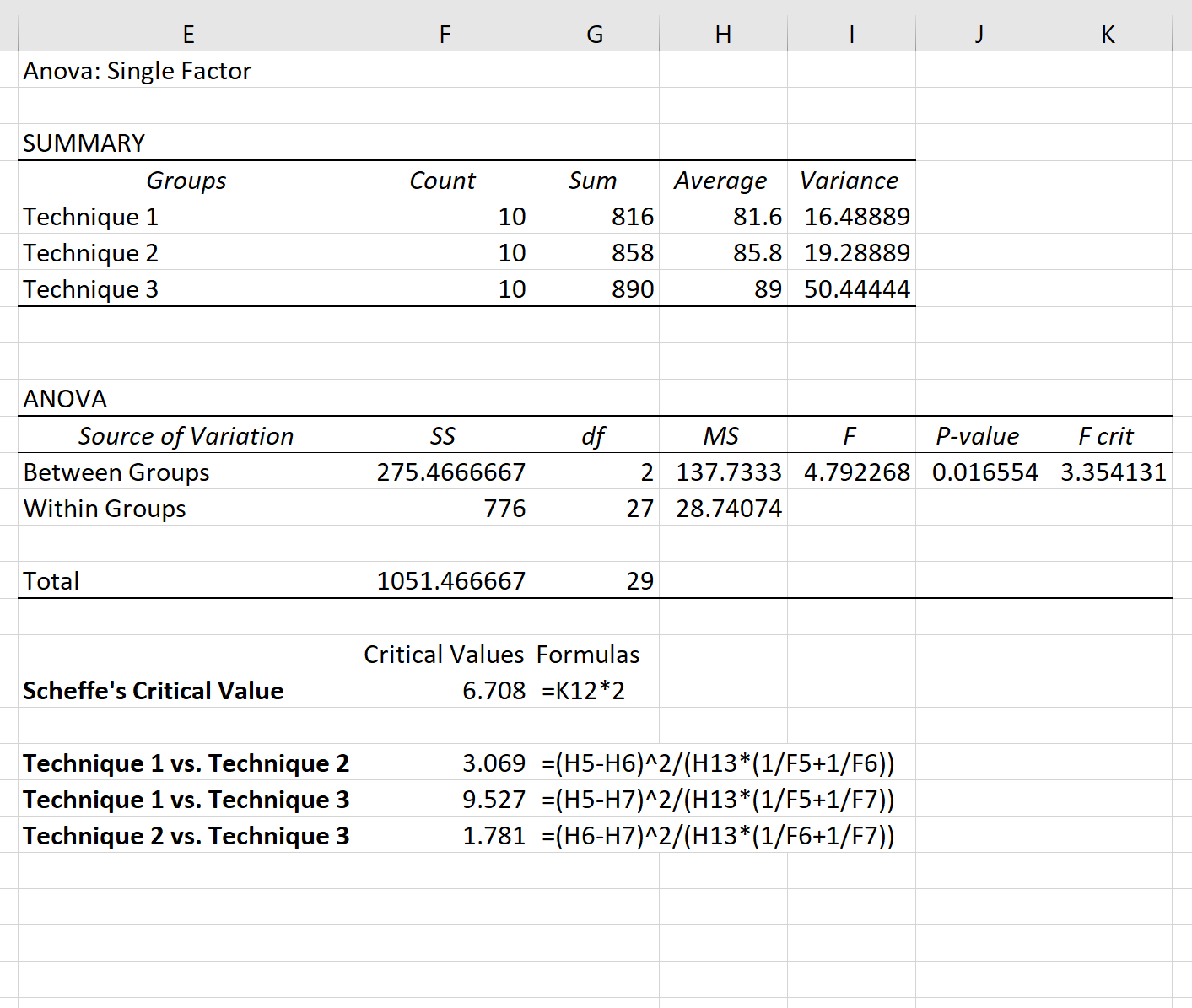
唯一超过 Scheffe 临界值的 F 统计量是技术 1 和技术 3 之间的比较。

因此，仅有的两个统计上显着不同的组是技术 1 和技术 3。

其他资源

如何在 Excel 中执行单向方差分析
如何在 Excel 中执行双向方差分析
如何在 Excel 中执行 Tukey-Kramer 事后检验