Excel:如何使用linest进行多元线性回归
您可以使用 Excel 中的LINEST函数将多元线性回归模型拟合到一组数据。
该函数使用以下基本语法:
= LINEST ( known_y's, [known_x's], [const], [stats] )
金子:
- known_y’s :已知 y 值的数组
- known_x’s :已知 x 值的数组
- const :可选参数。如果为 TRUE,则正常处理常数 b。如果为 FALSE,则常数 b 设置为 1。
- stats :可选参数。如果为 TRUE,则返回附加回归统计数据。如果为 FALSE,则不返回附加回归统计数据。
以下分步示例展示了如何在实践中使用此功能。
第 1 步:输入数据
首先,我们将以下数据集输入到 Excel 中:
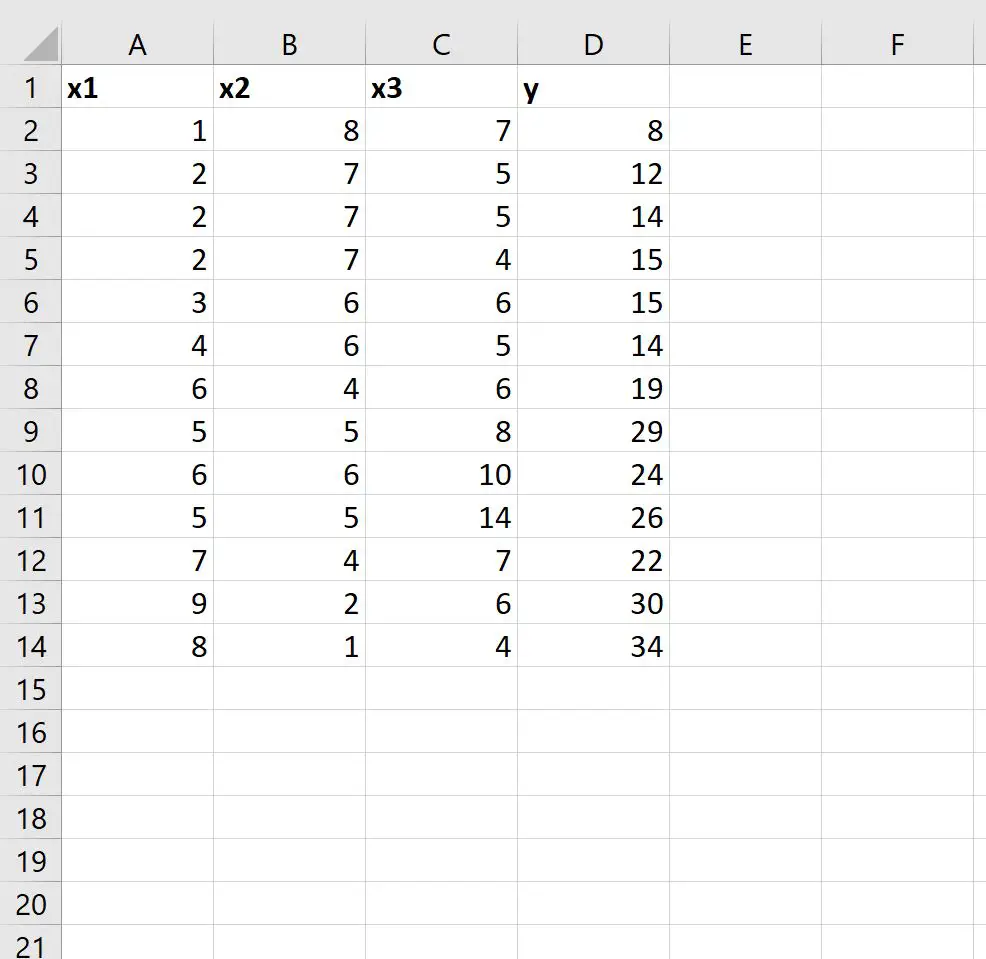
步骤 2:使用 LINEST 拟合多元线性回归模型
假设我们想要使用x1 、 x2和x3作为预测变量,使用y作为响应变量来拟合多元线性回归模型。
为此,我们可以在任何单元格中键入以下公式来拟合此多元线性回归模型
=LINEST( D2:D14 , A2:C14 )
以下屏幕截图显示了如何在实践中使用该公式:
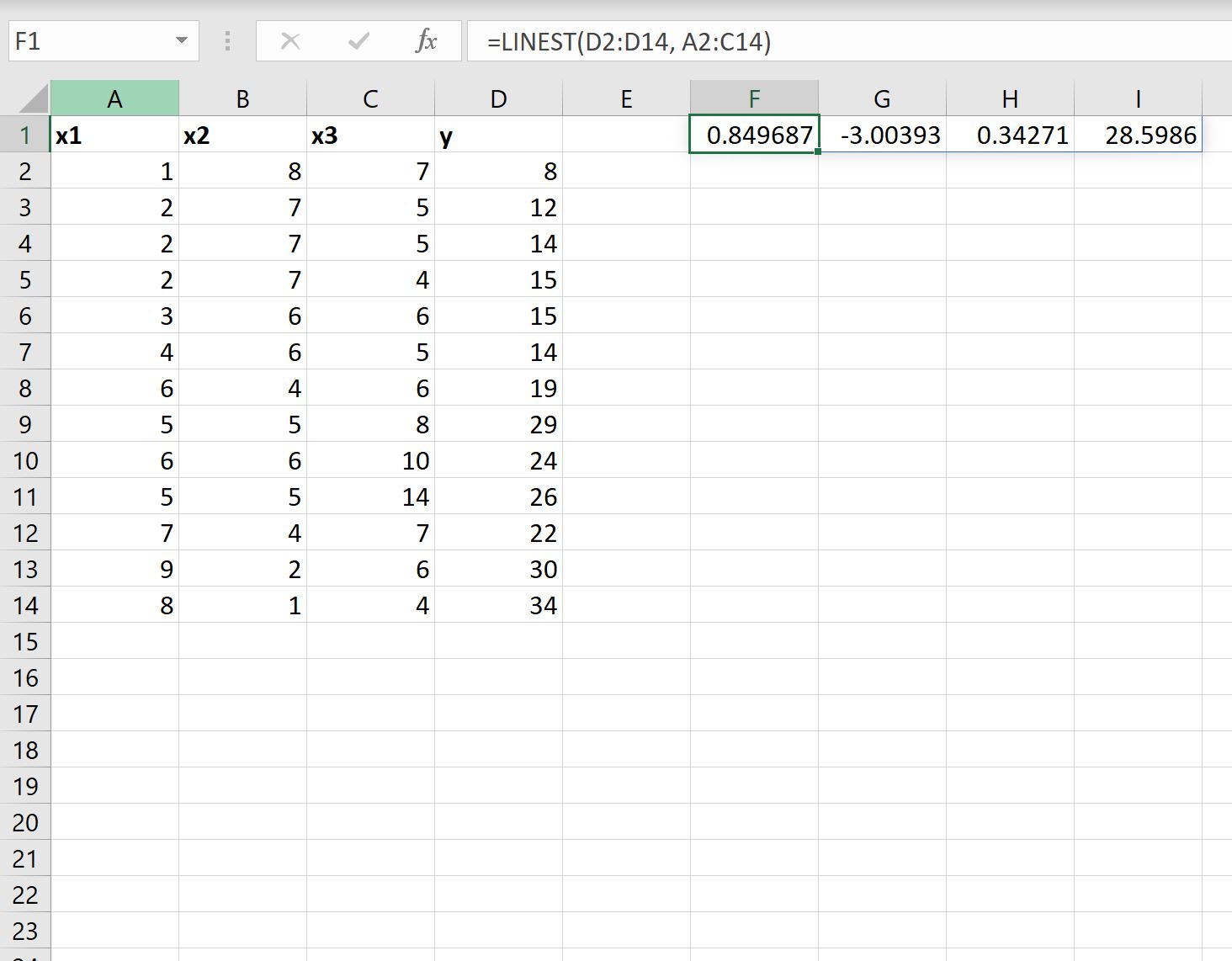
以下是如何解释结果:
- 截距系数为28.5986 。
- x1 的系数为0.34271 。
- x2 的系数为-3.00393 。
- x3 的系数为0.849687 。
使用这些系数,我们可以编写如下拟合回归方程:
y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)
步骤 3(可选):查看其他回归统计数据
我们还可以将LINEST函数中stats参数的值设置为TRUE ,以显示拟合回归方程的附加回归统计数据:
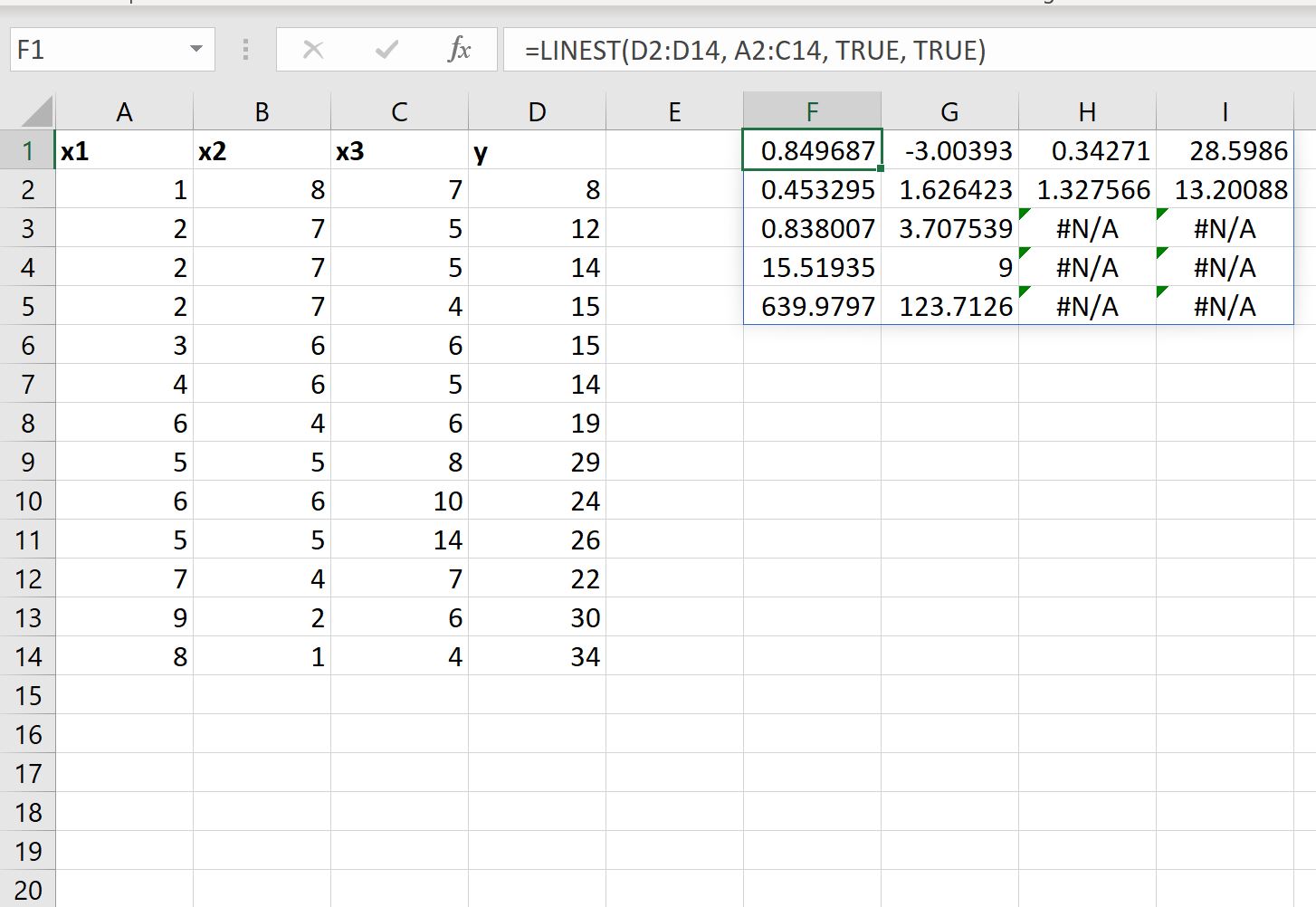
拟合的回归方程仍然相同:
y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)
以下是如何解释结果的其他值:
- x3 的标准误差是0.453295 。
- x2 的标准误差是1.626423 。
- x1 的标准误差是1.327566 。
- 截距的标准误差是13.20088 。
- 该型号的 R 2为.838007 。
- y 的残余标准误差为3.707539 。
- 总体 F 统计量为15.51925 。
- 自由度为9 。
- 回归平方和为639.9797 。
- 残差平方和为123.7126 。
一般来说,这些附加统计数据中最令人感兴趣的度量是 R 2值,它表示响应变量中可由预测变量解释的方差比例。
R 2的值可以在 0 到 1 之间变化。
由于该特定模型的 R 2为0.838 ,这告诉我们预测变量在预测响应变量 y 的值方面做得很好。
相关:什么是好的 R 平方值?
其他资源
以下教程介绍了如何在 Excel 中执行其他常见操作:
如何在 Excel 中使用 LOGEST 函数
如何在 Excel 中执行非线性回归
如何在 Excel 中执行三次回归