如何在 excel 中执行配对样本 t 检验
当一个样本中的每个观察值可以与另一个样本中的观察值相关联时,配对样本 t 检验用于比较两个样本的平均值。
本教程介绍如何在 Excel 中执行配对样本 t 检验。
如何在 Excel 中执行配对样本 t 检验
假设我们想知道某个课程是否对学生在特定考试中的表现有显着影响。为了测试这一点,我们要求一个班级 20 名学生进行预测试。然后我们让每个学生参加为期两周的课程。然后,学生重新参加类似难度的测试。
为了比较第一次和第二次测试的平均分数之间的差异,我们使用配对样本 t 检验,因为对于每个学生来说,他们在第一次测试中的分数可以与他们在第二次测试中的分数相关联。
下图显示了每个学生的前测成绩和后测成绩:
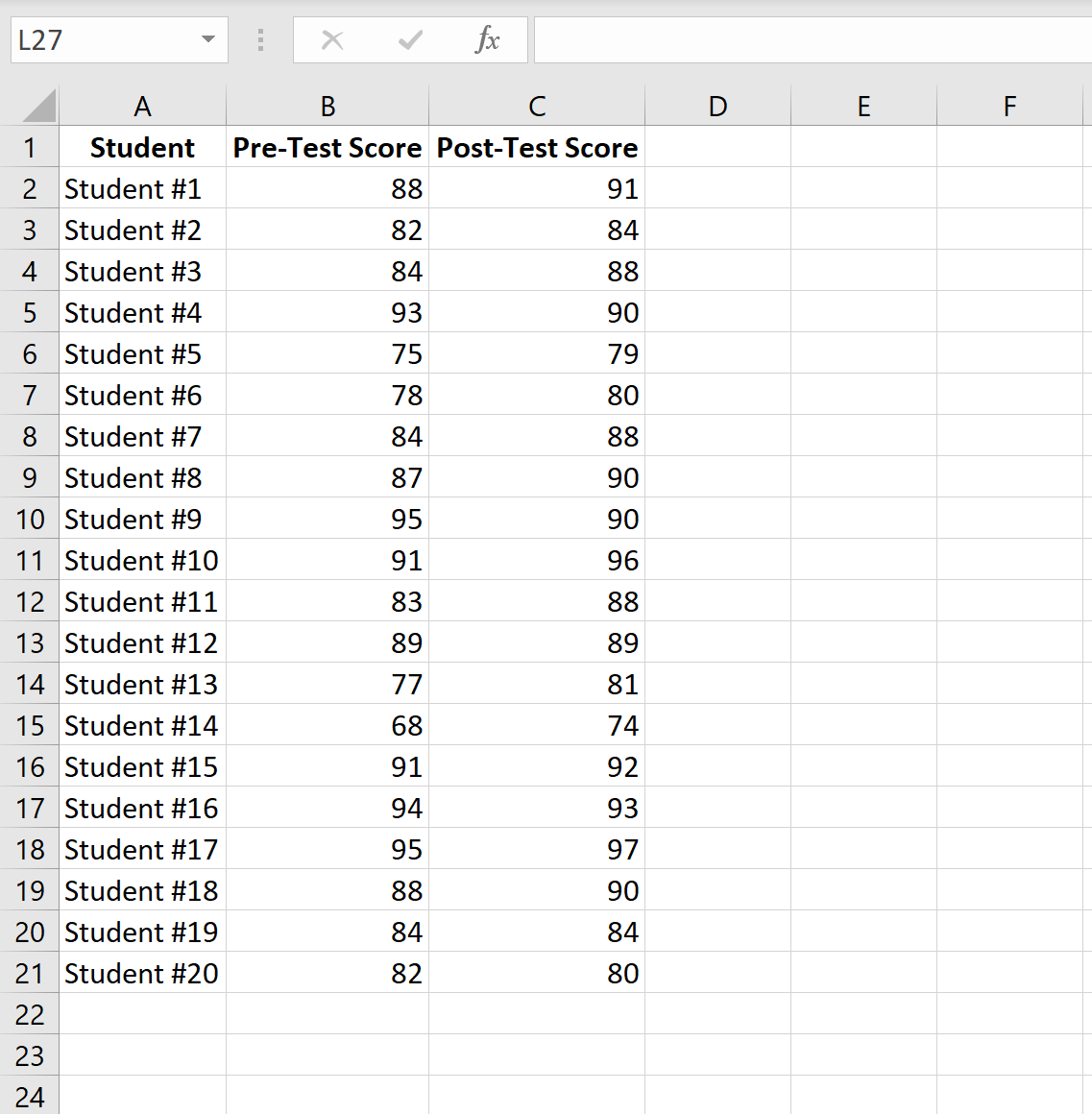
完成以下步骤来执行配对样本 t 检验,以确定测试前和测试后的平均测试分数是否存在显着差异。
步骤1:打开数据分析工具库。
在顶部功能区的“数据”选项卡中,单击“数据分析”。

如果您没有看到要单击的选项,则首先需要下载完全免费的分析工具库。
步骤 2:选择要使用的适当测试。
选择T 检验:均值配对两个样本 的选项,然后单击“确定”。
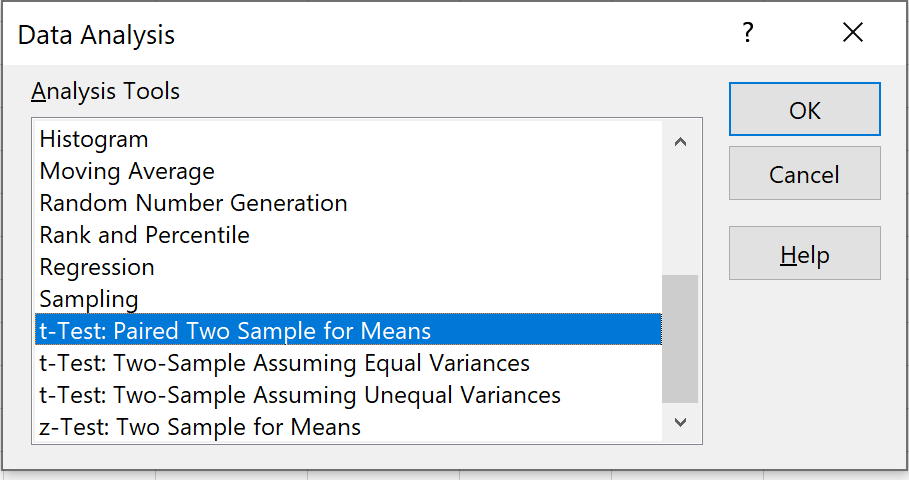
步骤 3:输入必要的信息。
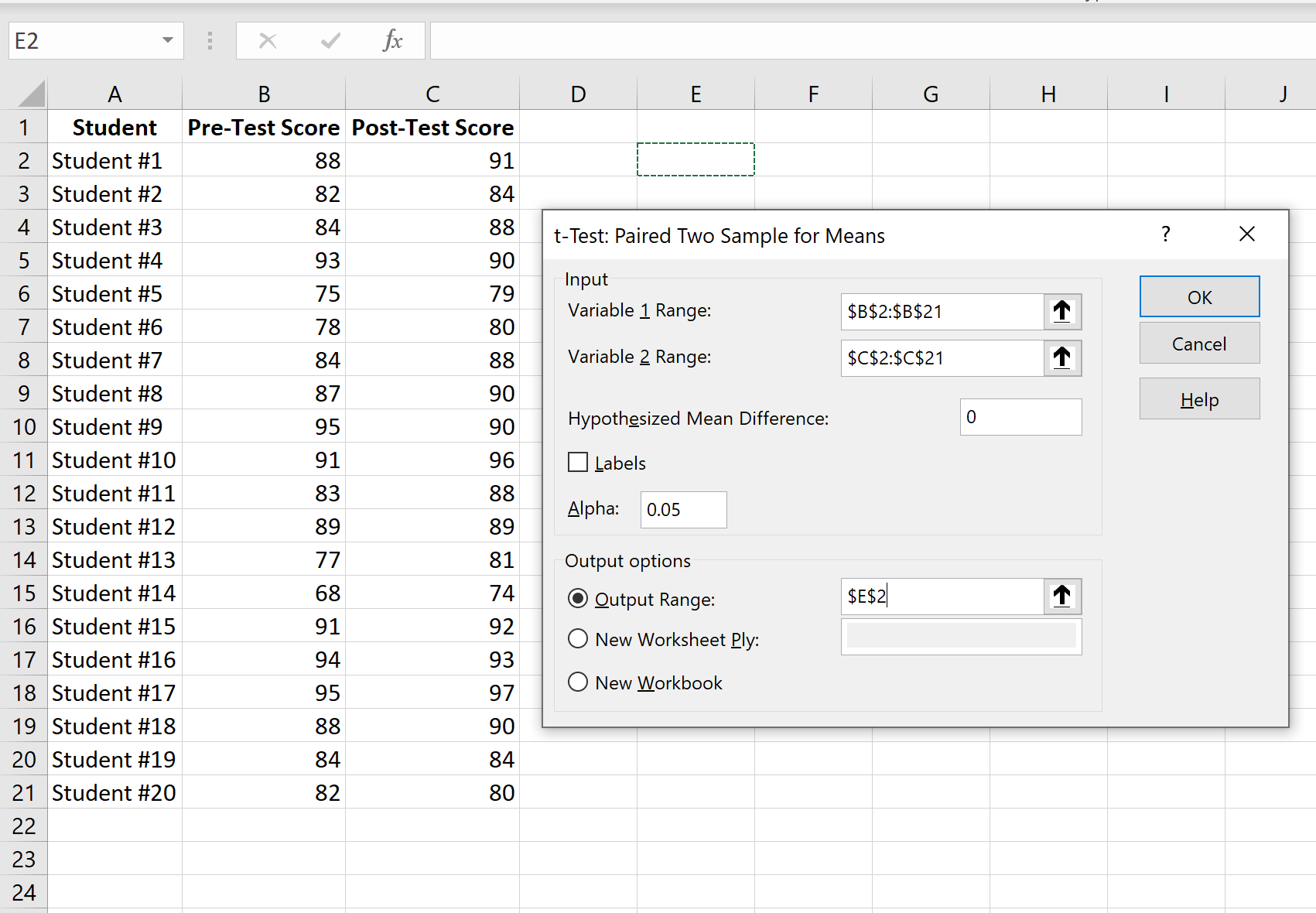
输入变量 1(测试前分数)、变量 2(测试后分数)、假设平均差(在本例中我们输入“0”,因为我们想知道真实差异是否测试前和测试后分数之间的平均值为 0),以及我们希望看到显示的测试结果的输出范围。然后单击“确定”。
第 4 步:解释结果。
在上一步中单击“确定”后,将显示 t 检验结果。
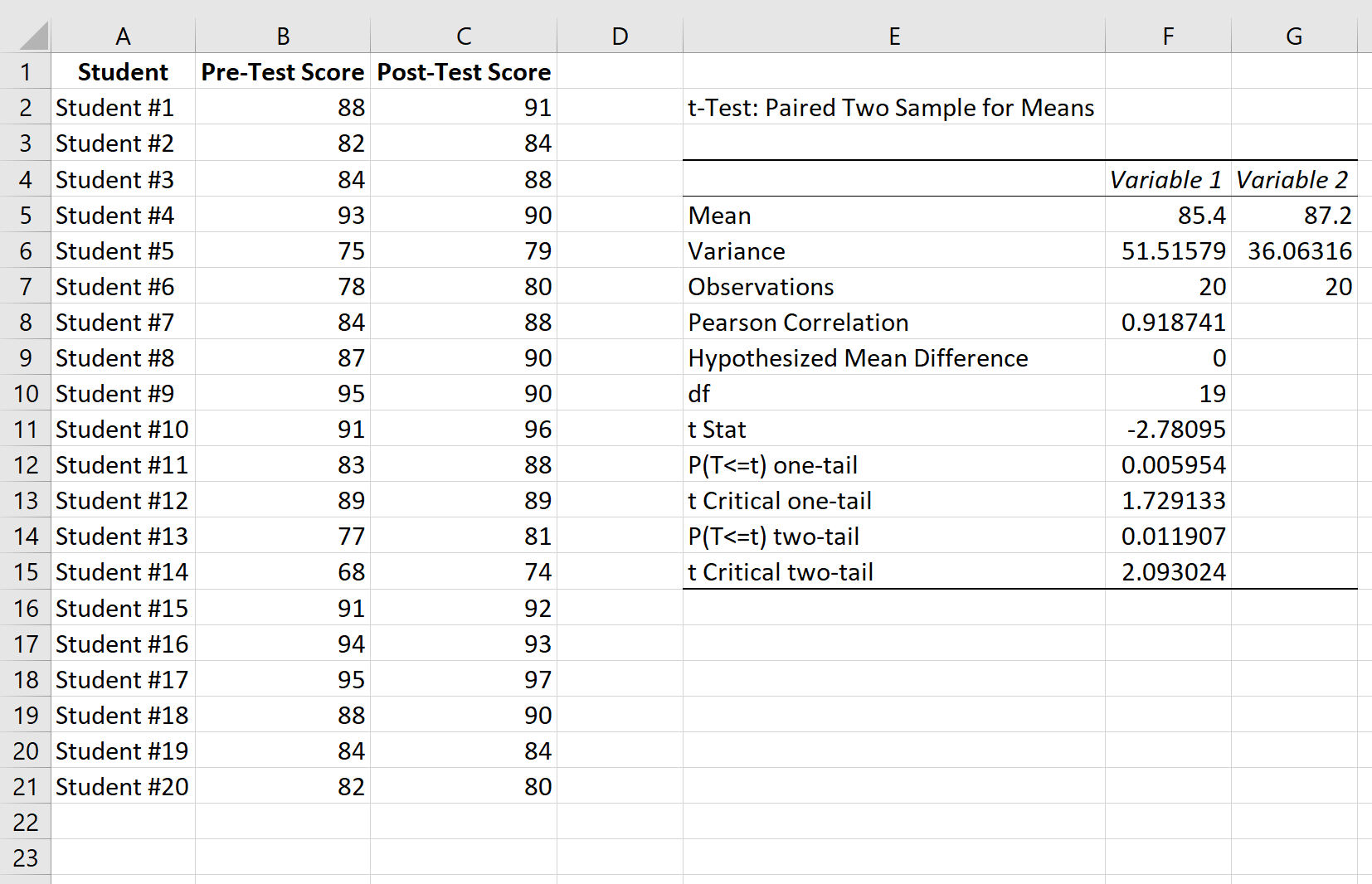
以下是如何解释结果:
平均值:这是每个样本的平均值。前测平均分85.4分,后测平均分87.2分。
方差:这是每个样本的方差。前测分数的方差为51.51 ,后测分数的方差为36.06 。
观察值:这是每个样本中的观察值数量。两个样本均包含20 个观察值。
皮尔逊相关性:测试前分数与测试后分数之间的相关性。结果是0.918 。
假设均值差:我们“假设”的数字是两个均值之间的差。在本例中,我们选择0 ,因为我们想要测试前测和后测分数之间是否存在差异。
df: t 检验的自由度。计算公式为 n-1,其中 n 是对的数量。在本例中,df = 20 – 1 = 19 。
t Stat: t检验统计量,结果为-2.78 。
双尾 P(T<=t):双尾 t 检验的 p 值。在这种情况下,p = 0.011907 。这小于 alpha = 0.05,因此我们拒绝原假设。我们有足够的证据表明,测试前和测试后的平均分数之间存在统计上的显着差异。
t 双尾临界:这是检验的临界值,通过识别 t 分布表中对应于 alpha = 0.05 和 df = 19 的双尾检验的值找到。结果是 2, 093024 。由于t检验统计量的绝对值大于该值,因此我们拒绝原假设。我们有足够的证据表明,测试前和测试后的平均分数之间存在统计上的显着差异。
请注意,p 值和临界值方法都会得出相同的结论。
其他资源
以下教程解释了如何在 Excel 中执行其他 t 检验: