如何在 excel 中构建预测区间
在统计学中, 简单线性回归是一种可以用来量化预测变量 x 和响应变量 y 之间关系的技术。
当我们执行简单的线性回归时,我们得到一条描述 x 和 y 之间关系的“最佳拟合线”,可以写为:
ŷ = b 0 + b 1 x
金子:
- ŷ 是响应变量的预测值
- b 0是 y 轴截距
- b 1是回归系数
- x 是预测变量的值
有时我们想使用这条最佳拟合线来构建给定值 x 0的预测区间,该区间是预测值 ŷ 0周围的一个区间,使得总体中 y 的真实值有 95% 的概率对应的x 0包含在该区间内。
计算给定值 x 0的预测区间的公式为:
× 0 +/- t α/2,df=n-2 * se
金子:
se = S yx √(1 + 1/n + (x 0 – x ) 2 /SS x )
这个公式可能看起来有点吓人,但实际上在 Excel 中计算起来很简单。接下来我们将看到一个使用此公式计算 Excel 中给定值的预测区间的示例。
示例:如何在 Excel 中构建预测区间
以下数据集显示了 15 名不同学生的学习小时数以及获得的考试成绩:
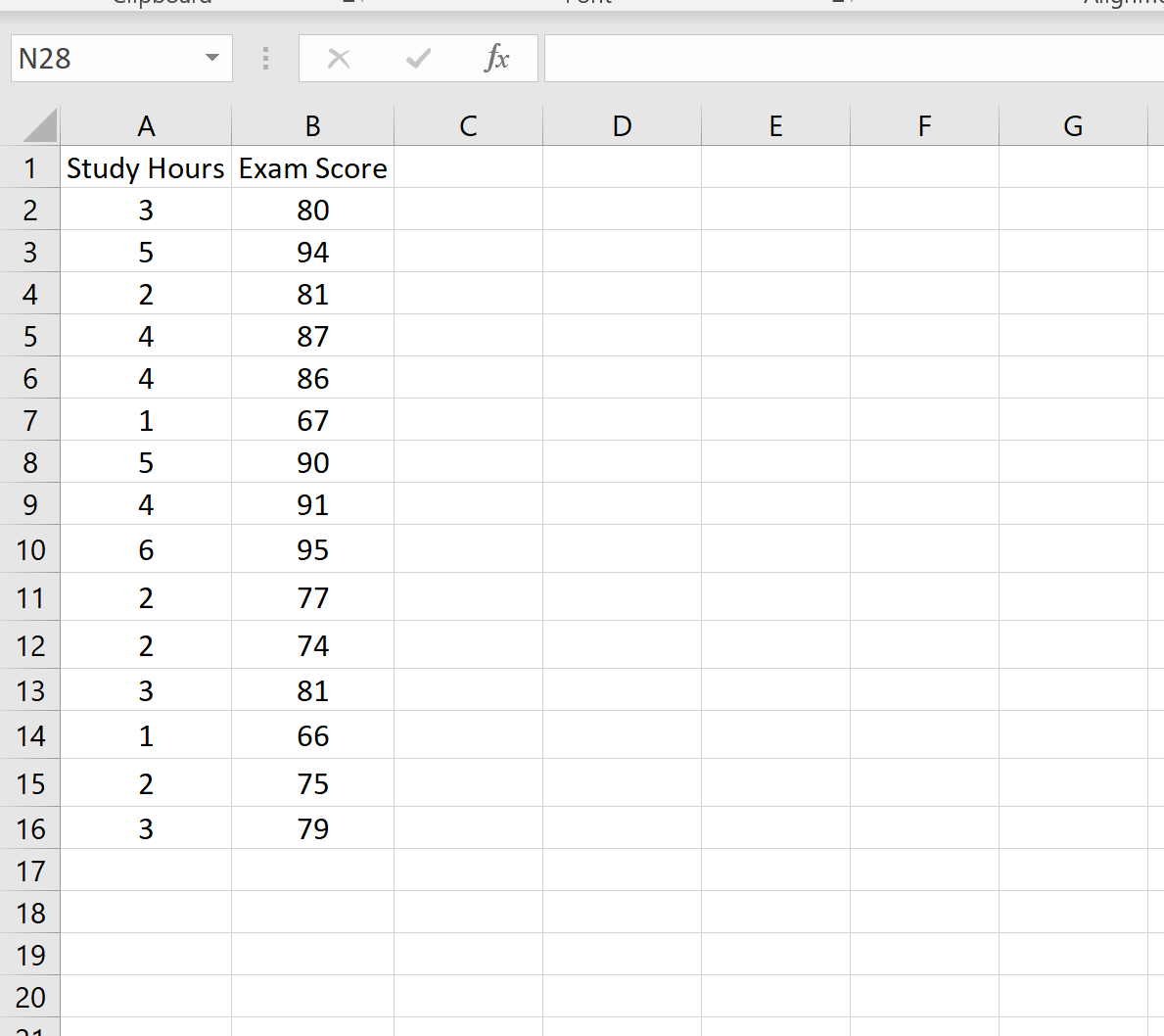
假设我们要为值 x 0 = 3 创建一个 95% 的预测区间。也就是说,我们要创建一个区间,使得对于学习以下课程的学生,考试成绩有 95% 的概率落入该区间内3小时。
下面的截图展示了如何计算获得这个预测区间所需的所有值。
注: F列中的公式显示了E列中的值是如何计算的。
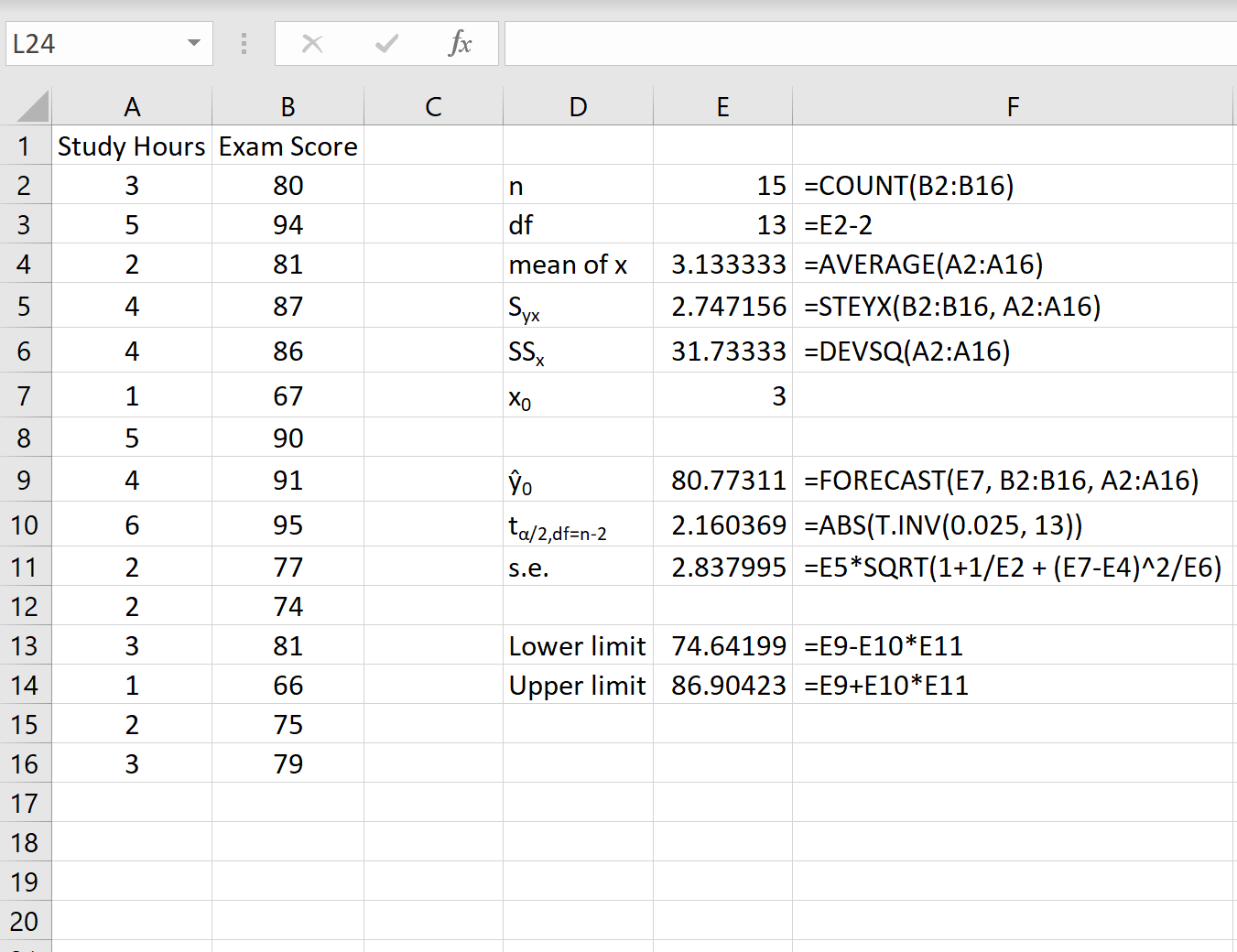
x 0 = 3 值的 95% 预测区间为(74.64, 86.90) 。也就是说,我们以 95% 的概率预测学习 3 小时的学生将获得 74.64 到 86.90 之间的分数。
关于所用计算的一些注释:
- 为了计算 t α/2,df=n-2 的 t 临界值,我们使用 α/2 = 0.05/2 = 0.25,因为我们想要 95% 的预测区间。请注意,较高的预测区间(例如,99% 的预测区间)将导致更宽的区间。相反,较小的预测区间(例如90%的预测区间)将导致较窄的区间。
- 我们使用公式=FORECAST()来获取 ŷ 0的预测值,但公式=FORECAST.LINEAR()将返回完全相同的值。