Python 中的 k 均值聚类：分步示例

机器学习中最常见的聚类算法之一称为k 均值聚类。

K 均值聚类是一种将数据集中的每个观察结果放入K个聚类中的一个技术。

最终目标是拥有K 个簇，其中每个簇内的观察结果彼此非常相似，而不同簇中的观察结果彼此非常不同。

在实践中，我们使用以下步骤来进行K-means聚类：

1. 选择K值。

• 首先，我们需要决定要在数据中识别多少个簇。通常我们只需要测试几个不同的K值并分析结果，看看对于给定问题，哪个簇数似乎最有意义。

2. 将每个观测值随机分配到一个初始簇（从 1 到K） 。

3. 执行以下过程，直到集群分配停止更改。

• 对于每个K个簇，计算该簇的重心。这只是第 k 个簇的观测值的p均值特征的向量。
• 将每个观测值分配给具有最近质心的簇。这里，最接近是使用欧几里德距离定义的。

以下分步示例展示了如何使用sklearn模块中的KMeans函数在 Python 中执行 k 均值聚类。

第1步：导入必要的模块

首先，我们将导入执行 k 均值聚类所需的所有模块：

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

第 2 步：创建数据框

接下来，我们将为 20 名不同的篮球运动员创建一个包含以下三个变量的 DataFrame：

• 点
• 帮助
• 反弹

以下代码显示了如何创建此 pandas DataFrame：

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#view first five rows of DataFrame
print ( df.head ())

   points assists rebounds
0 18.0 3.0 15
1 NaN 3.0 14
2 19.0 4.0 14
3 14.0 5.0 10
4 14.0 4.0 8

我们将使用 k 均值聚类根据这三个指标对相似的参与者进行分组。

第 3 步：清理并准备 DataFrame

然后我们将执行以下步骤：

• 使用dropna()删除任意列中具有 NaN 值的行
• 使用StandardScaler()将每个变量缩放为均值 0 和标准差 1。

以下代码展示了如何执行此操作：

 #drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

#view first five rows of scaled DataFrame
print (scaled_df[:5])

[[-0.86660275 -1.22683918 1.72722524]
 [-0.72081911 -0.96077767 1.45687694]
 [-1.44973731 -0.69471616 0.37548375]
 [-1.44973731 -0.96077767 -0.16521285]
 [-1.88708823 -0.16259314 1.45687694]]

注意：我们使用缩放，以便在拟合 k 均值算法时每个变量具有相同的重要性。否则，范围最宽的变量会产生太大的影响。

第 4 步：找到最佳簇数

要在 Python 中执行 k 均值聚类，我们可以使用sklearn模块中的KMeans函数。

该函数使用以下基本语法：

KMeans(init=’随机’, n_clusters=8, n_init=10, random_state=无)

金子：

• init ：控制初始化技术。
• n_clusters ：放置观测值的簇的数量。
• n_init ：要执行的初始化次数。默认运行 k-means 算法 10 次并返回 SSE 最低的那个。
• random_state ：您可以选择一个整数值以使算法结果可重现。

该函数最重要的参数是 n_clusters，它指定将观测值放入多少个簇中。

然而，我们事先并不知道有多少簇是最佳的，因此我们需要创建一个图表来显示簇的数量以及模型的 SSE（误差平方和）。

通常，当我们创建此类图时，我们会寻找平方和开始“弯曲”或趋于平坦的“拐点”。这通常是最佳的簇数。

以下代码展示了如何创建这种类型的图，该图在 x 轴上显示簇数，在 y 轴上显示 SSE：

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

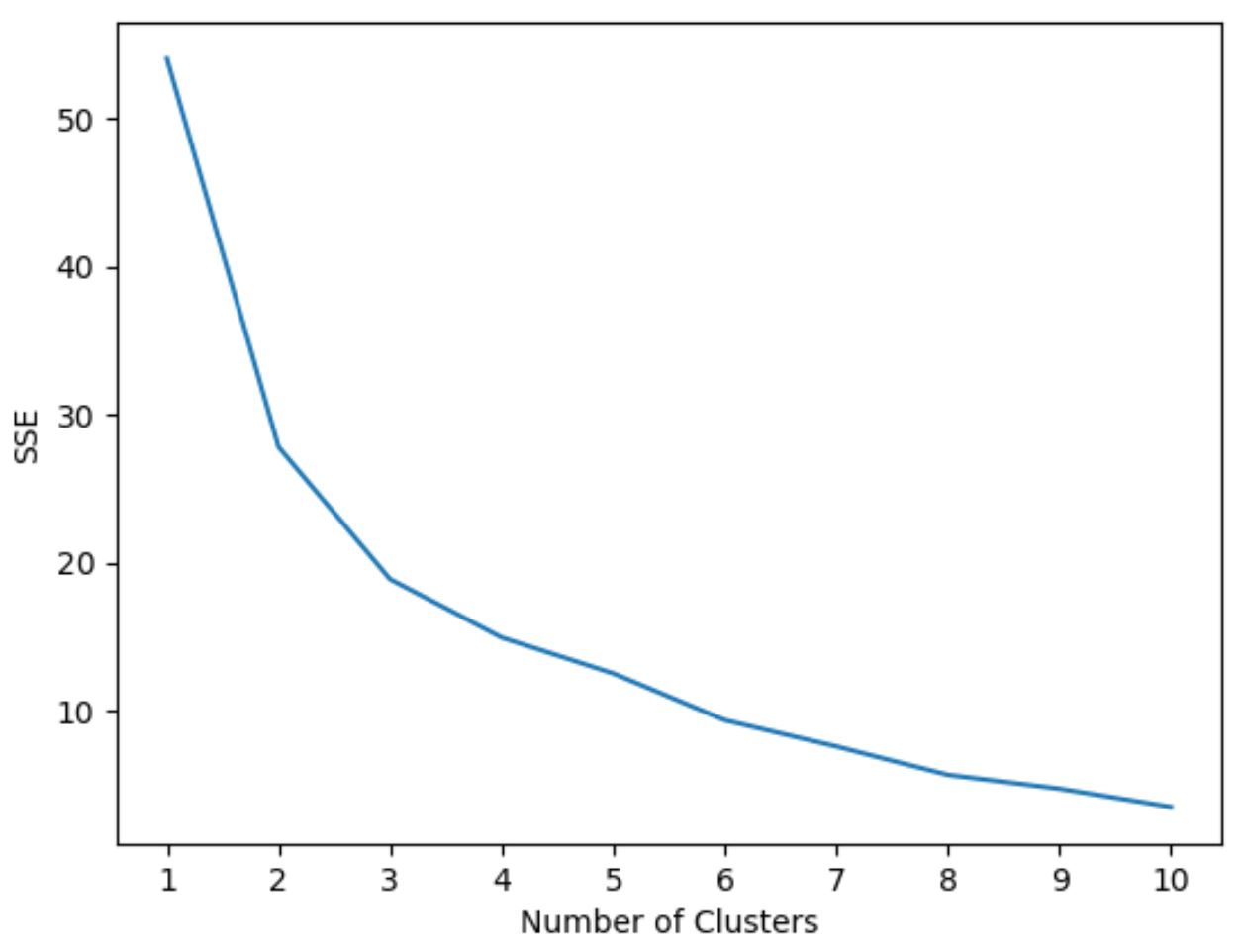
在此图中，似乎在 k = 3 个簇处存在扭结或“拐点”。

因此，在下一步拟合 k 均值聚类模型时，我们将使用 3 个聚类。

注意：在现实世界中，建议结合使用此图和领域专业知识来选择要使用的集群数量。

步骤 5：使用最佳K执行 K 均值聚类

以下代码展示了如何使用k的最佳值 3 对数据集执行 k 均值聚类：

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

结果表显示了 DataFrame 中每个观察值的聚类分配。

为了使这些结果更易于解释，我们可以在 DataFrame 中添加一列来显示每个玩家的集群分配：

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

集群列包含每个玩家分配到的集群编号（0、1 或 2）。

属于同一簇的球员的得分、助攻和篮板数列的值大致相似。

注意：您可以在此处找到sklearn的KMeans函数的完整文档。

其他资源

以下教程解释了如何在 Python 中执行其他常见任务：

如何在 Python 中执行线性回归
如何在 Python 中执行逻辑回归
如何在Python中执行K-Fold交叉验证