Mae 对比rmse:您应该使用哪个指标?
回归模型用于量化一个或多个预测变量与响应变量之间的关系。
每当我们拟合回归模型时,我们都想了解模型能够如何很好地使用预测变量的值来预测响应变量的值。
我们经常用来量化模型对数据集的拟合程度的两个指标是平均绝对误差 (MAE) 和均方根误差 (RMSE),其计算如下:
MAE :告诉我们数据集中预测值与实际值之间的平均绝对差的指标。 MAE 越低,模型越适合数据集。
MAE = 1/n * Σ|y i – ŷ i |
金子:
- Σ是一个符号,意思是“和”
- y i是第 i 个观测值的观测值
- ŷ i是第 i个观测值的预测值
- n 是样本量
RMSE :一种度量,告诉我们数据集中预测值与实际值之间的均方根差的平方根。 RMSE 越低,模型越适合数据集。
计算方法如下:
RMSE = √ Σ(y i – ŷ i ) 2 / n
金子:
- Σ是一个符号,意思是“和”
- ŷ i是第 i个观测值的预测值
- y i是第 i 个观测值的观测值
- n 是样本量
示例:RMSE 和 MAE 的计算
假设我们使用回归模型来预测 10 名球员在一场篮球比赛中会得分多少分。
下表显示了模型预测的得分与球员实际得分的比较:

使用MAE计算器,我们可以计算出MAE为3.2。
这告诉我们,模型预测值与实际值之间的平均绝对差为 3.2。
使用RMSE 计算器,我们可以计算出 RMSE 等于4 。
这告诉我们,预测得分与实际得分之间的均方根差的平方根是 4。
请注意,每个指标都让我们了解模型的预测值与数据集中的实际值之间的典型差异,但每个指标的解释略有不同。
RMSE 与 MAE:您应该使用哪个指标?
如果您想为远离均值的观测值分配更多权重(即,如果偏差 20 的严重程度是偏差 10 的两倍以上),则最好使用 RMSE 来测量误差,因为 RMSE 是对远离平均值的观察结果更加敏感。
但是,如果“偏移”为 20 的情况是“偏移”为 10 的两倍,那么最好使用 MAE。
为了说明这一点,假设我们有一名在得分方面明显异常的球员:
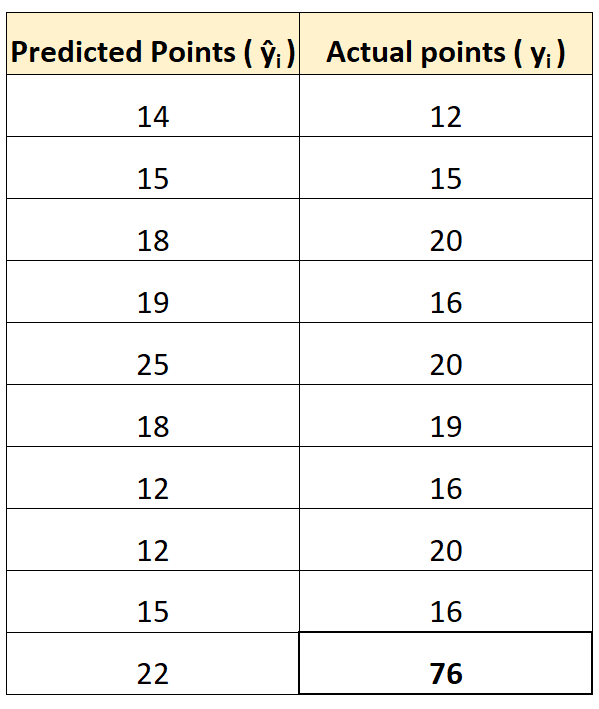
使用前面提到的在线计算器,我们可以计算 MAE 和 RMSE 为:
- 硕士:8
- 均方根误差:16.4356
请注意,RMSE 的增幅远大于 MAE。
这是因为 RMSE 在其公式中使用了平方差,而观测值 76 和预测值 22 之间的平方差相当大。这导致 RMSE 值显着增加。
在实践中,我们通常将多个回归模型拟合到一个数据集,并为每个模型仅计算其中一个指标。
例如,我们可以拟合三个不同的回归模型并计算每个模型的 RMSE。然后,我们会选择 RMSE 值最低的模型作为“最佳”模型,因为它的预测最接近数据集中的实际值。
无论哪种情况,只需确保为每个模型计算相同的指标即可。例如,不要计算一个模型的 MAE 和另一模型的 RMSE,然后比较这两个测量值。
其他资源
以下教程解释了如何使用不同的统计软件计算 MAE:
如何在 Excel 中计算平均绝对误差
如何计算 R 中的平均绝对误差
如何用 Python 计算平均绝对误差
以下教程解释了如何使用不同的统计软件计算 RMSE: