如何在 python 中执行 ols 回归（附示例）

普通最小二乘 (OLS) 回归是一种方法，可让我们找到最能描述一个或多个预测变量与响应变量之间关系的直线。

该方法使我们能够找到以下方程：

ŷ = b ₀ + b ₁ x

金子：

• ŷ : 估计响应值
• b ₀ ：回归线的原点
• b ₁ ：回归线的斜率

该方程可以帮助我们理解预测变量和响应变量之间的关系，并且可以用于在给定预测变量值的情况下预测响应变量的值。

以下分步示例展示了如何在 Python 中执行 OLS 回归。

第 1 步：创建数据

在此示例中，我们将为 15 名学生创建一个包含以下两个变量的数据集：

• 学习总时数
• 考试成绩

我们将执行 OLS 回归，使用小时作为预测变量，使用考试成绩作为响应变量。

以下代码展示了如何在 pandas 中创建这个假数据集：

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

步骤 2：执行 OLS 回归

接下来，我们可以使用statsmodels模块中的函数来执行 OLS 回归，使用小时作为预测变量，得分作为响应变量：

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

从coef列中，我们可以看到回归系数并写出以下拟合回归方程：

分数 = 65.334 + 1.9824*（小时）

这意味着每多学习一小时，平均考试成绩就会增加1.9824分。

原始值65,334告诉我们零学习时间的学生的平均预期考试成绩。

我们还可以使用这个方程根据学生学习的小时数找到预期的考试成绩。

例如，学习 10 小时的学生应获得85.158的考试成绩：

分数 = 65.334 + 1.9824*(10) = 85.158

以下是如何解释模型摘要的其余部分：

• P(>|t|)：这是与模型系数相关的 p 值。由于小时数(0.000) 的 p 值小于 0.05，因此我们可以说小时数和分数之间存在统计上显着的关联。
• R 平方：这告诉我们，考试成绩的变化百分比可以通过学习的小时数来解释。在这种情况下， 83.1%的分数差异可以用学习时间来解释。
• F 统计量和 p 值： F 统计量 ( 63.91 ) 和相应的 p 值 ( 2.25e-06 ) 告诉我们回归模型的整体显着性，即模型中的预测变量是否有助于解释变异。在响应变量中。由于此示例中的 p 值小于 0.05，因此我们的模型具有统计显着性，并且小时数被认为有助于解释分数变化。

第 3 步：可视化最佳拟合线

最后，我们可以使用matplotlib数据可视化包来可视化拟合到实际数据点的回归线：

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

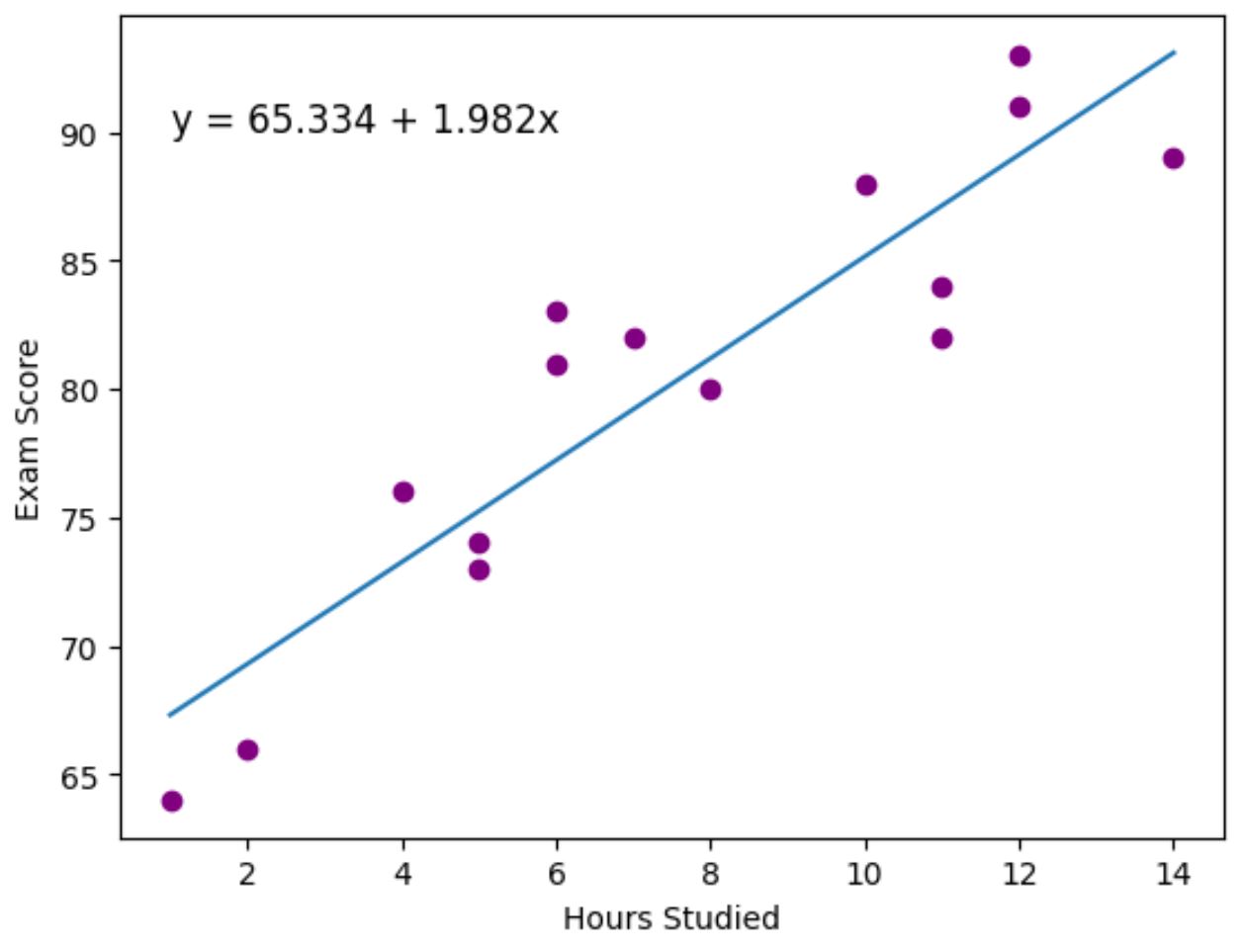
紫色点代表实际数据点，蓝色线代表拟合回归线。

我们还使用plt.text()函数将拟合的回归方程添加到图的左上角。

从图表中可以看出，拟合的回归线很好地捕捉了小时变量和分数变量之间的关系。

其他资源

以下教程解释了如何在 Python 中执行其他常见任务：

如何在 Python 中执行逻辑回归
如何在 Python 中执行指数回归
如何用Python计算回归模型的AIC