Python 中的偏最小二乘法（一步一步）

机器学习中最常见的问题之一是多重共线性。当数据集中的两个或多个预测变量高度相关时，就会发生这种情况。

发生这种情况时，模型可能能够很好地拟合训练数据集，但它可能在从未见过的新数据集上表现不佳，因为它与训练数据集过度拟合。训练集。

解决这个问题的一种方法是使用一种称为 偏最小二乘法的方法，其工作原理如下：

• 标准化预测变量和响应变量。
• 计算p 个原始预测变量的M 个线性组合（称为“PLS 分量”），这些组合解释了响应变量和预测变量中的大量变化。
• 使用最小二乘法拟合线性回归模型，并使用 PLS 分量作为预测变量。
• 使用k 折交叉验证来找到模型中保留的 PLS 组件的最佳数量。

本教程提供了如何在 Python 中执行偏最小二乘法的分步示例。

第1步：导入必要的包

首先，我们将导入在 Python 中执行偏最小二乘法所需的包：

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

第2步：加载数据

在此示例中，我们将使用名为mtcars的数据集，其中包含 33 辆不同汽车的信息。我们将使用hp作为响应变量，并使用以下变量作为预测变量：

• 英里/加仑
• 展示
• 拉屎
• 重量
• 快秒

以下代码展示了如何加载和显示此数据集：

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

步骤 3：拟合偏最小二乘模型

以下代码显示了如何使 PLS 模型适合此数据。

请注意， cv = RepeatedKFold()告诉 Python 使用k 折交叉验证来评估模型性能。对于本例，我们选择 k = 10 次，重复 3 次。

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

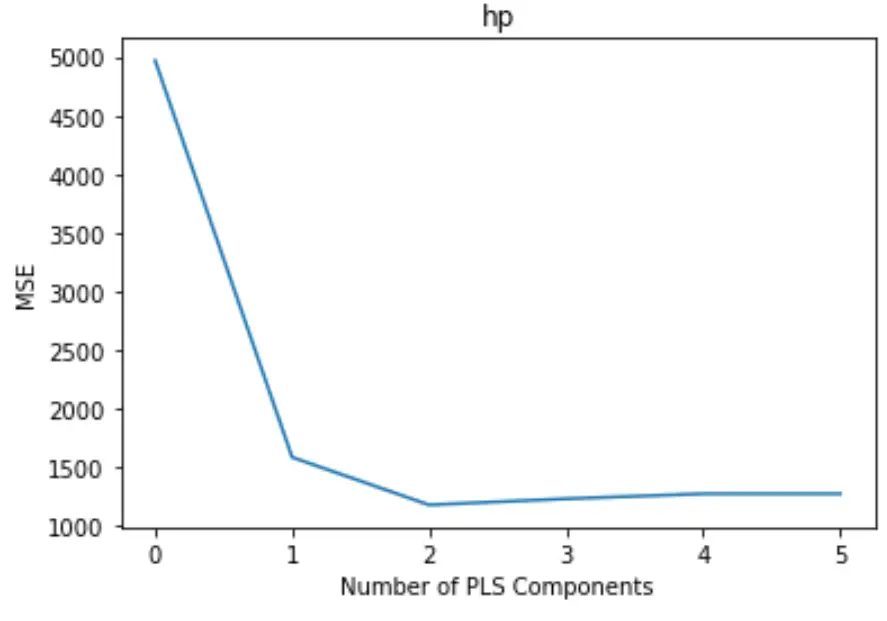
该图沿 x 轴显示 PLS 分量的数量，沿 y 轴显示 MSE（均方误差）测试。

从图中我们可以看到，通过添加两个 PLS 组件，测试的 MSE 会下降，但当我们添加两个以上的 PLS 组件时，MSE 就会开始增加。

因此，最优模型仅包含前两个 PLS 分量。

第 4 步：使用最终模型进行预测

我们可以使用具有两个 PLS 组件的最终 PLS 模型来对新观测值进行预测。

以下代码展示了如何将原始数据集拆分为训练集和测试集，并使用具有两个 PLS 组件的 PLS 模型对测试集进行预测。

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

我们看到测试的 RMSE 结果为29.9094 。这是测试集观测值的预测hp值和观察到的hp值之间的平均偏差。

此示例中使用的完整 Python 代码可以在此处找到。