如何在 python 中创建协方差矩阵
协方差是衡量一个变量的变化与第二个变量的变化如何关联的指标。更具体地说,它是两个变量线性相关程度的度量。
协方差矩阵是一个方阵,显示许多不同变量之间的协方差。这是了解数据集中不同变量如何关联的有用方法。
以下示例演示如何在 Python 中创建协方差矩阵。
如何在 Python 中创建协方差矩阵
使用以下步骤在 Python 中创建协方差矩阵。
步骤 1:创建数据集。
首先,我们将创建一个数据集,其中包含 10 名不同学生在数学、科学和历史这三个科目中的考试成绩。
import numpy as np math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95] science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94] history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78] data = np.array([math, science, history])
步骤 2:创建协方差矩阵。
接下来,我们将使用 numpy cov()函数创建该数据集的协方差矩阵,并指定bias = True ,以便我们可以计算总体协方差矩阵。
np.cov(data, bias= True )
array([[ 64.96, 33.2, -24.44],
[33.2, 56.4, -24.1],
[-24.44, -24.1, 75.56]])
步骤 3:解释协方差矩阵。
矩阵对角线上的值就是每个受试者的方差。例如:
- 数学成绩的方差为 64.96
- 科学分数的方差为 56.4
- 历史分数方差为 75.56
矩阵的其他值代表不同主体之间的协方差。例如:
- 数学和科学分数之间的协方差为 33.2。
- 数学和历史分数之间的协方差为-24.44。
- 科学和历史分数之间的协方差为-24.1。
协方差为正数表示两个变量倾向于同时增加或减少。例如,数学和科学具有正协方差 (33.2),表明数学得分高的学生也往往在科学得分高。相反,数学成绩不佳的学生在科学方面也往往表现不佳。
协方差为负数表示随着一个变量的增加,第二个变量趋于减少。例如,数学和历史具有负协方差(-24.44),表明数学得分高的学生往往在历史得分较低。相反,数学成绩低的学生往往历史成绩高。
步骤 4:可视化协方差矩阵(可选)。
您可以使用seaborn包的heatmap()函数可视化协方差矩阵:
import seaborn as sns import matplotlib.pyplot as plt cov = np.cov(data, bias=True) labs = ['math', 'science', 'history'] sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs) plt.show()
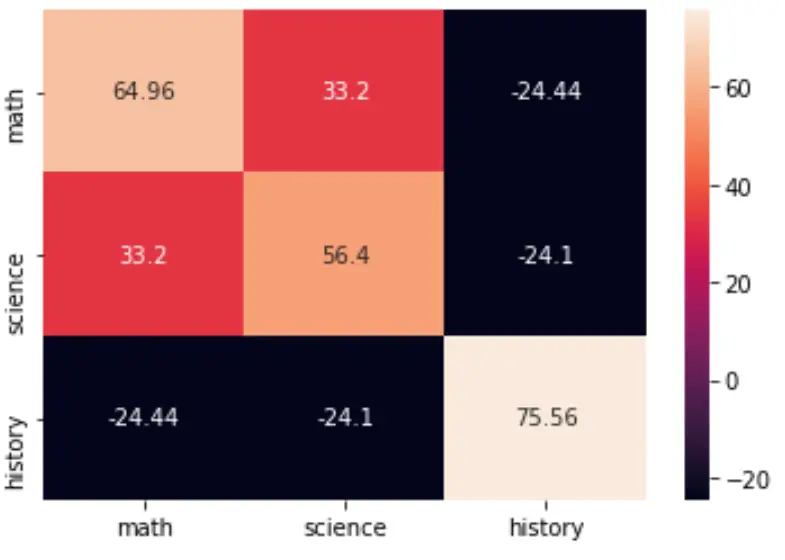
您还可以通过指定cmap参数来更改调色板:
sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show()
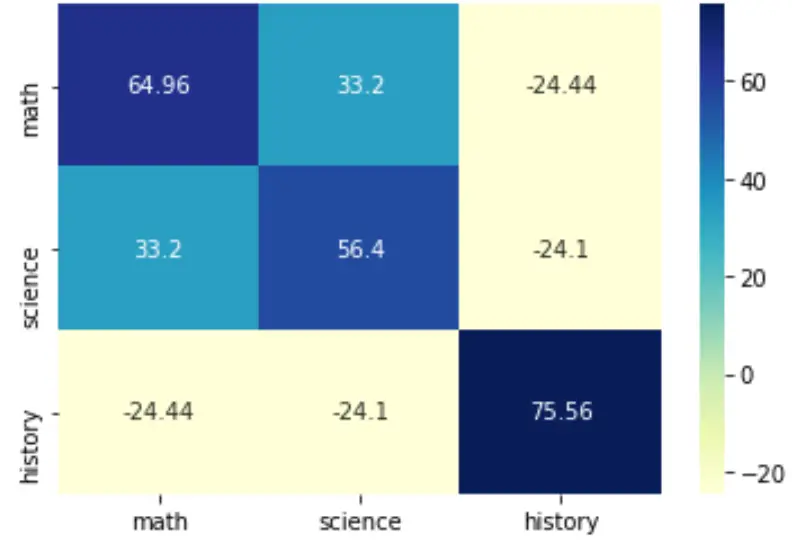
有关如何设置此热图样式的更多详细信息,请参阅seaborn 文档。