如何在 python 中创建相关矩阵

量化两个变量之间关系的一种方法是使用Pearson 相关系数，它是两个变量之间线性关联的度量。

它的值介于 -1 和 1 之间，其中：

• -1 表示完全负线性相关。
• 0 表示没有线性相关。
• 1 表示完全正线性相关。

相关系数离零越远，两个变量之间的相关性越强。

但在某些情况下，我们想要了解多对变量之间的相关性。在这些情况下，我们可以创建一个相关矩阵，它是一个方表，显示变量的多个成对组合之间的相关系数。

本教程介绍如何在 Python 中创建和解释相关矩阵。

如何在 Python 中创建相关矩阵

使用以下步骤在 Python 中创建相关矩阵。

步骤 1：创建数据集。

 import pandas as pd

data = {'assists': [4, 5, 5, 6, 7, 8, 8, 10],
        'rebounds': [12, 14, 13, 7, 8, 8, 9, 13],
        'points': [22, 24, 26, 26, 29, 32, 20, 14]
        }

df = pd. DataFrame (data, columns=['assists','rebounds','points'])
df

   assist rebound points
0 4 12 22
1 5 14 24
2 5 13 26
3 6 7 26
4 7 8 29
5 8 8 32
6 8 9 20
7 10 13 14

步骤 2：创建相关矩阵。

 #create correlation matrix
df. corr ()

                assists rebound points
assists 1.000000 -0.244861 -0.329573
rebounds -0.244861 1.000000 -0.522092
points -0.329573 -0.522092 1.000000

#create same correlation matrix with coefficients rounded to 3 decimals 
df. corr (). round (3)
	       assists rebound points
assists 1.000 -0.245 -0.330
rebounds -0.245 1.000 -0.522
points -0.330 -0.522 1.000

步骤 3：解释相关矩阵。

沿表对角线的相关系数均等于 1，因为每个变量与其自身完全相关。

所有其他相关系数表示变量的不同成对组合之间的相关性。例如：

• 助攻和篮板之间的相关系数为-0.245 。
• 助攻数与得分之间的相关系数为-0.330 。
• 篮板数与得分之间的相关系数为-0.522 。

步骤 4：可视化相关矩阵（可选）。

您可以使用 pandas 中提供的样式选项可视化相关矩阵：

 corr = df. corr ()
corr. style . background_gradient (cmap='coolwarm')

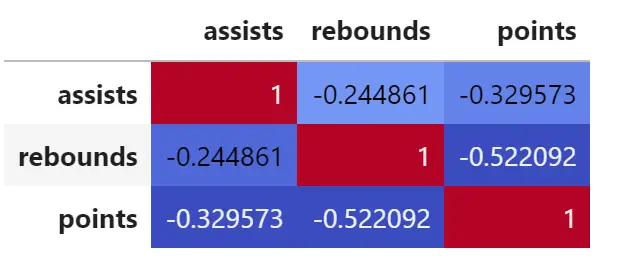
您还可以修改cmap参数以生成具有不同颜色的相关矩阵。

 corr = df. corr ()
corr. style . background_gradient (cmap=' RdYlGn ') 

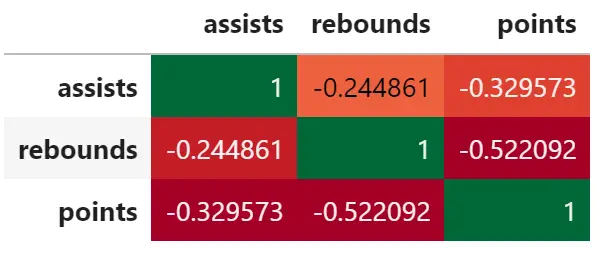
 corr = df. corr ()
corr. style . background_gradient (cmap=' bwr ') 

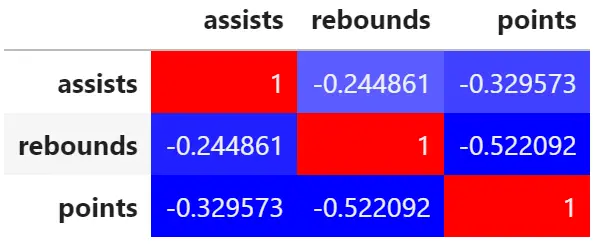
 corr = df. corr ()
corr. style . background_gradient (cmap=' PuOr ') 

注意：有关cmap参数的完整列表，请参阅matplotlib 文档。