如何在 python 中执行分位数回归

线性回归是一种我们可以用来理解一个或多个预测变量与响应变量之间关系的方法。

通常，当我们执行线性回归时，我们想要估计响应变量的平均值。

但是，我们可以使用一种称为分位数回归的方法来估计响应值的任何分位数或百分位数，例如第 70 个百分位数、第 90 个百分位数、第 98 个百分位数等。

本教程提供了如何使用此函数在 Python 中执行分位数回归的分步示例。

第1步：加载必要的包

首先，我们将加载必要的包和函数：

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

第 2 步：创建数据

在此示例中，我们将创建一个数据集，其中包含一所大学 100 名学生的学习时间和考试结果：

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

步骤 3：执行分位数回归

接下来，我们将使用学习时间作为预测变量和考试成绩作为响应变量来拟合分位数回归模型。

我们将使用该模型根据学习小时数来预测预期的 90% 考试成绩：

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

从结果中我们可以看到估计的回归方程：

考试成绩的第 90 个百分位数 = 59.6104 + 2.8495*（小时）

例如，所有学习 8 小时的学生的第 90 个百分位数分数应为 82.4：

考试成绩的第 90 个百分位数 = 59.6104 + 2.8495*(8) = 82.4 。

输出还显示预测变量的截距和时间的置信上限和下限。

第 4 步：可视化结果

我们还可以通过创建散点图来可视化回归结果，并将拟合的分位数回归方程叠加在图表上：

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

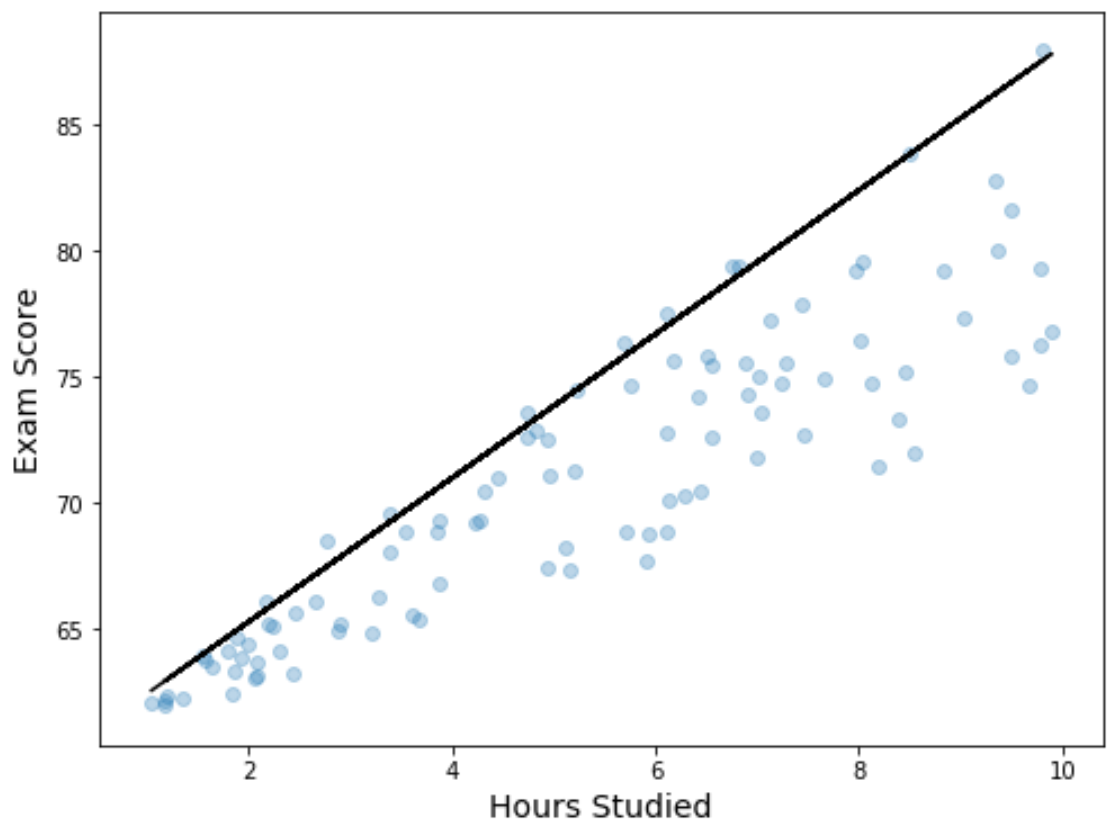
与简单的线性回归线不同，请注意，这条拟合线并不代表数据的“最佳拟合线”。相反，它会通过预测变量每个水平的估计第 90 个百分位。

其他资源

如何在 Python 中执行简单线性回归
如何在 Python 中执行二次回归