如何在 python 中执行双变量分析:带有示例
术语双变量分析是指对两个变量的分析。你可以记住这一点,因为前缀“bi”的意思是“二”。
双变量分析的目标是了解两个变量之间的关系
执行双变量分析的常用方法有以下三种:
1.点云
2.相关系数
3.简单线性回归
以下示例展示了如何使用以下 pandas DataFrame 在 Python 中执行每种类型的双变量分析,其中包含有关两个变量的信息: (1)学习时间和(2) 20 名不同学生获得的考试成绩:
import pandas as pd #createDataFrame df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 8], ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82, 80, 88, 85, 90, 92, 94, 94, 88, 91, 96]}) #view first five rows of DataFrame df. head () hours score 0 1 75 1 1 66 2 1 68 3 2 74 4 2 78
1. 点云
我们可以使用以下语法来创建学习时间与考试结果的散点图:
import matplotlib. pyplot as plt #create scatterplot of hours vs. score plt. scatter (df. hours , df. score ) plt. title (' Hours Studied vs. Exam Score ') plt. xlabel (' Hours Studied ') plt. ylabel (' Exam Score ')
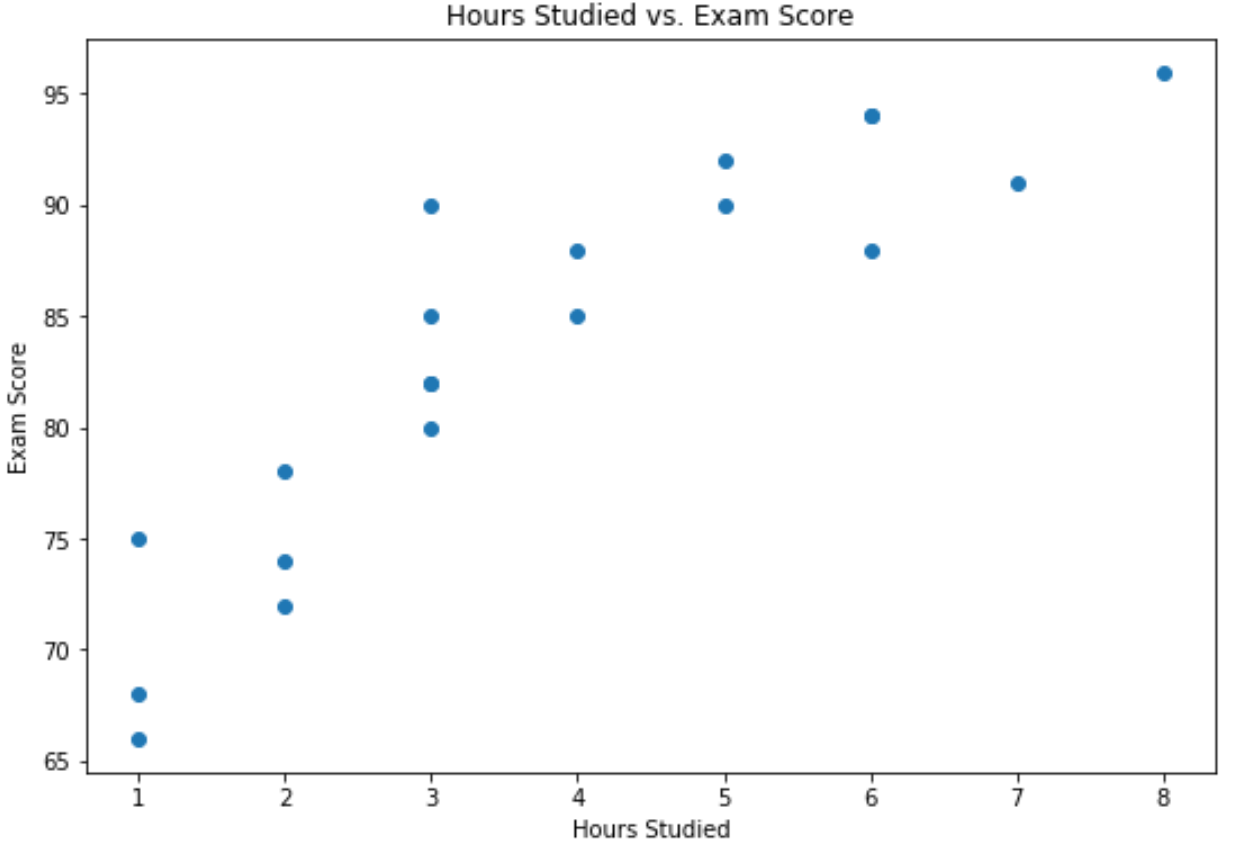
x 轴显示学习时间,y 轴显示考试成绩。
该图显示,两个变量之间存在正相关关系:随着学习时数的增加,考试成绩也趋于增加。
2. 相关系数
皮尔逊相关系数是一种量化两个变量之间线性关系的方法。
我们可以使用 pandas 中的corr()函数来创建相关矩阵:
#create correlation matrix df. corr () hours score hours 1.000000 0.891306 score 0.891306 1.000000
相关系数为0.891 。这表明学习时间和考试成绩之间存在很强的正相关关系。
3. 简单线性回归
简单线性回归是一种统计方法,我们可以用来量化两个变量之间的关系。
我们可以使用 statsmodels 包中的OLS()函数来快速拟合一个简单的线性回归模型,用于学习时间和收到的考试结果:
import statsmodels. api as sm #define response variable y = df[' score '] #define explanatory variable x = df[[' hours ']] #add constant to predictor variables x = sm. add_constant (x) #fit linear regression model model = sm. OLS (y,x). fit () #view model summary print ( model.summary ()) OLS Regression Results ==================================================== ============================ Dept. Variable: R-squared score: 0.794 Model: OLS Adj. R-squared: 0.783 Method: Least Squares F-statistic: 69.56 Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07 Time: 16:15:52 Log-Likelihood: -55,886 No. Observations: 20 AIC: 115.8 Df Residuals: 18 BIC: 117.8 Model: 1 Covariance Type: non-robust ==================================================== ============================ coef std err t P>|t| [0.025 0.975] -------------------------------------------------- ---------------------------- const 69.0734 1.965 35.149 0.000 64.945 73.202 hours 3.8471 0.461 8.340 0.000 2.878 4.816 ==================================================== ============================ Omnibus: 0.171 Durbin-Watson: 1.404 Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177 Skew: 0.165 Prob(JB): 0.915 Kurtosis: 2.679 Cond. No. 9.37 ==================================================== ============================
拟合后的回归方程为:
考试成绩 = 69.0734 + 3.8471*(学习时间)
这告诉我们,每多学习一小时,考试成绩就会平均提高3.8471 。
我们还可以使用拟合回归方程根据学习的总小时数来预测学生将获得的分数。
例如,学习 3 小时的学生应该得到81.6147的分数:
- 考试成绩 = 69.0734 + 3.8471*(学习时间)
- 考试成绩 = 69.0734 + 3.8471*(3)
- 考试成绩 = 81.6147
其他资源
以下教程提供有关双变量分析的其他信息: