如何在 python 中测试正态性（4 种方法）

许多统计测试假设数据集呈正态分布。

在 Python 中检查这个假设有四种常见方法：

1.（可视化方法）创建直方图。

• 如果直方图近似为“钟形”形状，则假定数据呈正态分布。

2.（可视化方法）创建QQ图。

• 如果图上的点大致沿直线对角线分布，则假定数据呈正态分布。

3.（正式统计检验）执行 Shapiro-Wilk 检验。

• 如果检验的 p 值大于 α = 0.05，则假定数据呈正态分布。

4.（正式统计检验）执行 Kolmogorov-Smirnov 检验。

• 如果检验的 p 值大于 α = 0.05，则假定数据呈正态分布。

以下示例展示了如何在实践中使用每种方法。

方法 1：创建直方图

以下代码显示如何为遵循对数正态分布的数据集创建直方图：

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

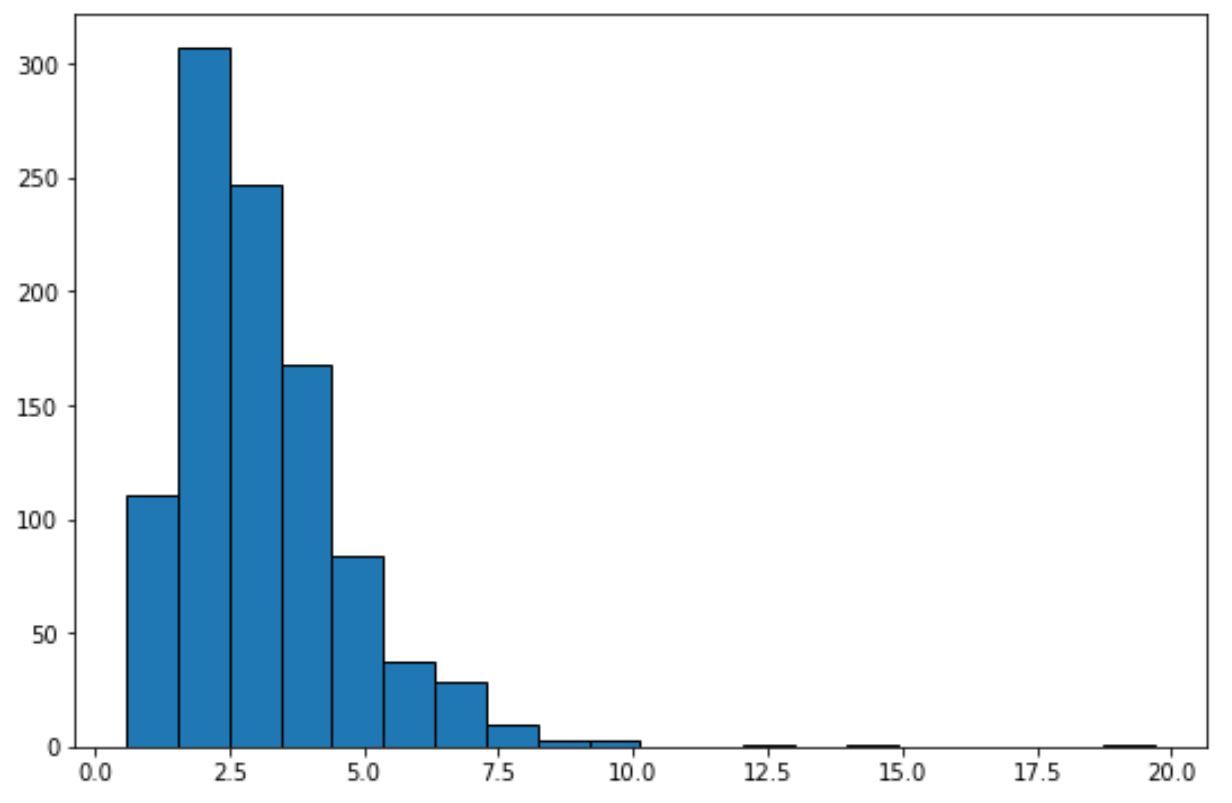
只需查看这个直方图，我们就可以看出数据集没有表现出“钟形”并且不呈正态分布。

方法2：创建QQ图

以下代码显示如何为遵循对数正态分布的数据集创建 QQ 图：

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

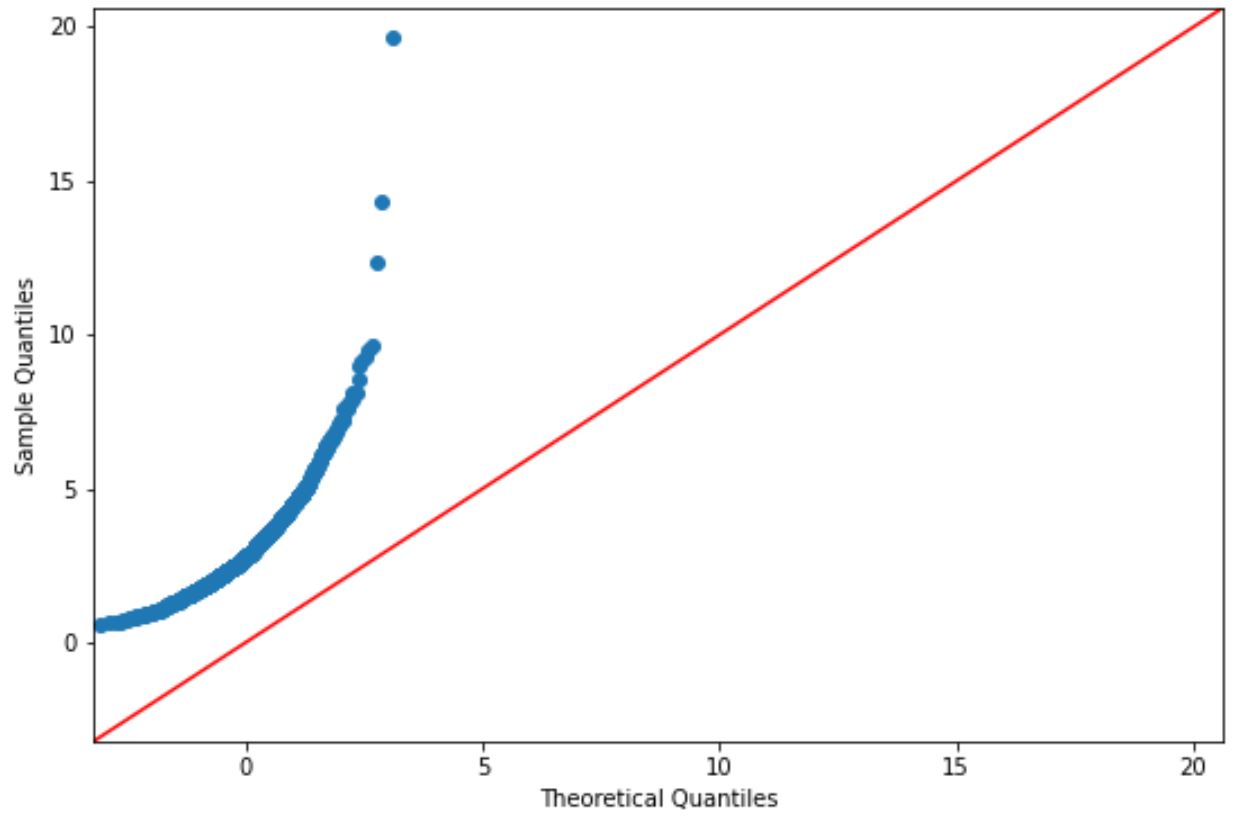
如果绘图点大致位于一条直线对角线上，我们通常假设数据集呈正态分布。

然而，该图上的点显然与红线不对应，因此我们不能假设该数据集是正态分布的。

鉴于我们使用对数正态分布函数生成数据，这应该是有意义的。

方法 3：执行 Shapiro-Wilk 检验

以下代码显示如何对遵循对数正态分布的数据集执行 Shapiro-Wilk：

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

从结果中，我们可以看到检验统计量为0.857 ，相应的 p 值为3.88e-29 （非常接近于零）。

由于 p 值小于 0.05，我们拒绝 Shapiro-Wilk 检验的原假设。

这意味着我们有足够的证据表明样本数据并非来自正态分布。

方法 4：执行 Kolmogorov-Smirnov 检验

以下代码显示如何对遵循对数正态分布的数据集执行 Kolmogorov-Smirnov 检验：

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

从结果中，我们可以看到检验统计量为0.841 ，相应的 p 值为0.0 。

由于 p 值小于 0.05，我们拒绝 Kolmogorov-Smirnov 检验的原假设。

这意味着我们有足够的证据表明样本数据并非来自正态分布。

如何处理非正态数据

如果给定的数据集不是正态分布的，我们通常可以执行以下转换之一以使其更加正态分布：

1.对数变换：将x值变换为log(x) 。

2. 平方根变换：将x的值变换为√x 。

3.立方根变换：将x的值变换为x ^1/3 。

通过执行这些转换，数据集通常变得更加正态分布。

阅读本教程以了解如何在 Python 中执行这些转换。