如何在 python 中创建残差图

残差图是一种显示回归模型残差拟合值的图。

这种类型的图通常用于评估线性回归模型是否适合给定的数据集并检查残差的异方差性。

本教程介绍如何在 Python 中为线性回归模型创建残差图。

示例：Python 中的残差图

在本例中，我们将使用一个描述 10 名篮球运动员属性的数据集：

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

简单线性回归的残差图

假设我们使用点作为预测变量、等级作为响应变量来拟合一个简单的线性回归模型：

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

我们可以使用 statsmodels 库中的plot_regress_exog() 函数创建残差图或拟合图：

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

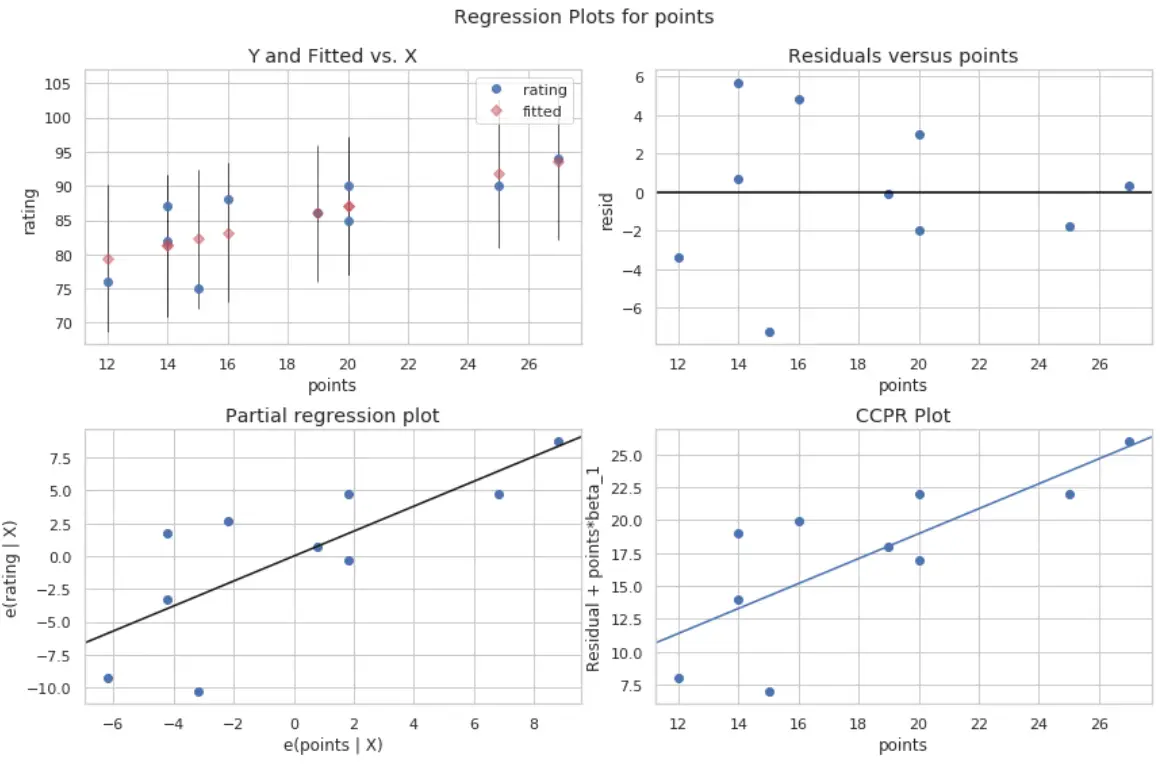
产生了四个地块。右上角的是残差图与调整后的图。该图上的 x 轴显示预测变量点的实际值，y 轴显示该值的残差。

由于残差似乎随机分散在零附近，这表明异方差性不是预测变量的问题。

多元线性回归的残差图

假设我们使用助攻和篮板作为预测变量、评分作为响应变量来拟合多元线性回归模型：

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

再次，我们可以使用 statsmodels 库中的plot_regress_exog() 函数为每个单独的预测变量创建残差与预测变量图。

例如，这就是预测变量Assist的残差/预测图的样子：

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

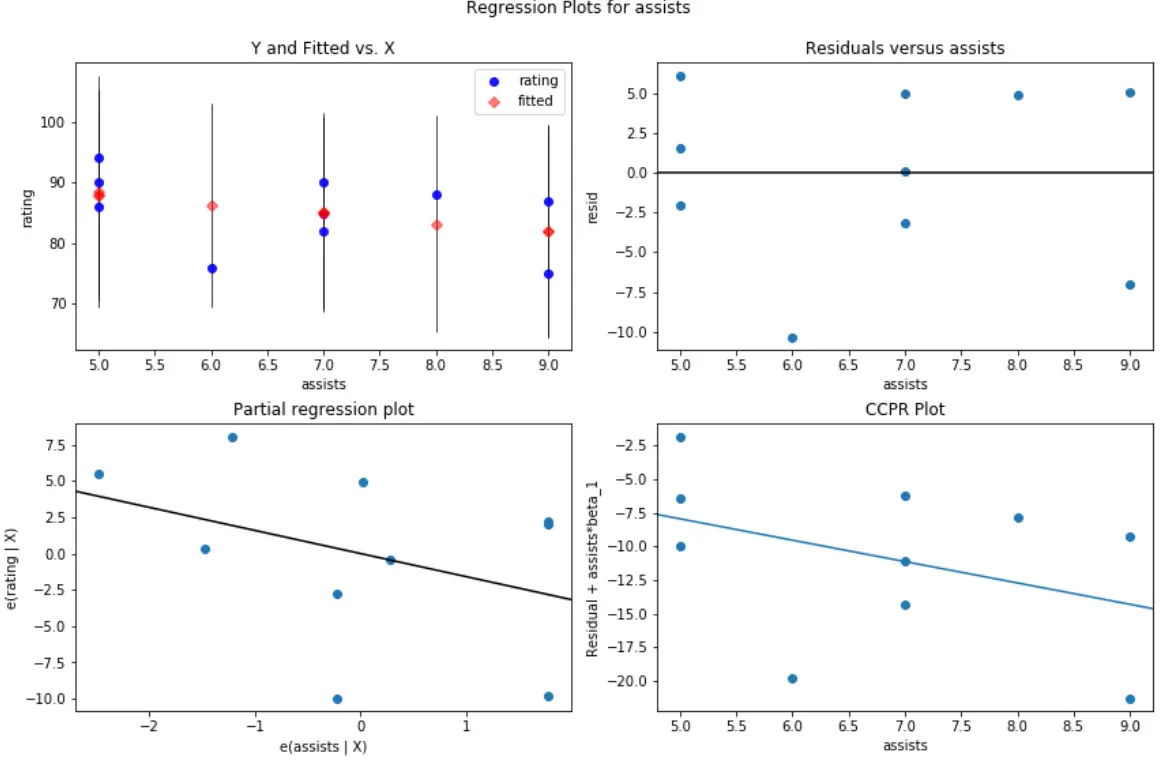
这就是预测变量反弹的残差/预测图的样子：

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

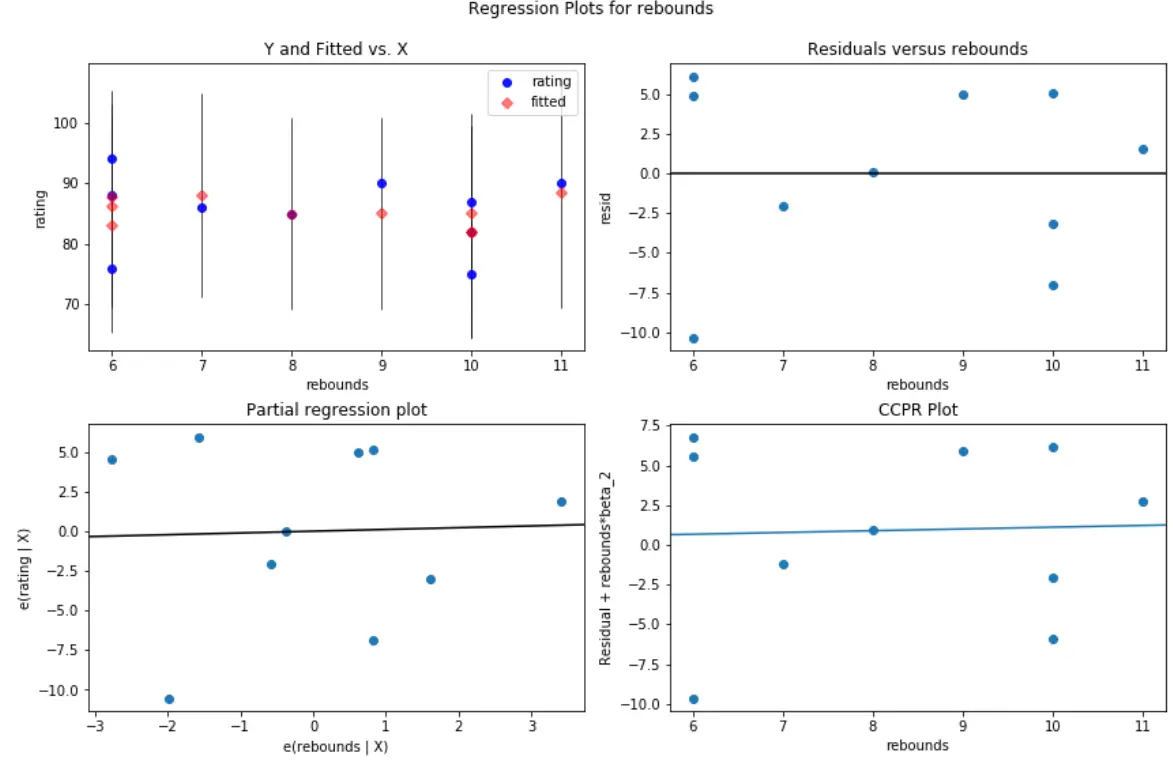
在这两个图中，残差似乎随机分散在零附近，表明异方差性不是模型中任何预测变量的问题。