如何在python中计算学生化残差

学生残差只是残差除以其估计的标准差。

在实践中，我们通常说数据集中学生残差绝对值大于 3 的任何观测值都是异常值。

我们可以使用 statsmodels 的OLSResults.outlier_test()函数快速获取 Python 中回归模型的学生化残差，该函数使用以下语法：

OLSResults.outlier_test()

其中OLSResults是使用 statsmodels ols()函数拟合的线性模型的名称。

示例：Python 中学生化残差的计算

假设我们用 Python 构建以下简单线性回归模型：

 #import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels. api as sm
from statsmodels. formula . api import ols

#create dataset
df = pd. DataFrame ({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]})

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

我们可以使用outlier_test()函数生成一个 DataFrame，其中包含数据集中每个观察值的学生化残差：

 #calculate studentized residuals
stud_res = model. outlier_test ()

#display studentized residuals
print(stud_res)

    student_resid unadj_p bonf(p)
0 -0.486471 0.641494 1.000000
1 -0.491937 0.637814 1.000000
2 0.172006 0.868300 1.000000
3 1.287711 0.238781 1.000000
4 0.106923 0.917850 1.000000
5 0.748842 0.478355 1.000000
6 -0.968124 0.365234 1.000000
7 -2.409911 0.046780 0.467801
8 1.688046 0.135258 1.000000
9 -0.014163 0.989095 1.000000

此 DataFrame 显示数据集中每个观察值的以下值：

• 学生化残留
• 学生化残差的未调整 p 值
• 学生残差的 Bonferroni 校正 p 值

我们可以看到数据集中第一个观察的学生化残差是-0.486471 ，第二个观察的学生化残差是-0.491937 ，依此类推。

我们还可以创建预测变量值与相应学生化残差的快速绘图：

 import matplotlib. pyplot as plt

#define predictor variable values and studentized residuals
x = df[' points ']
y = stud_res[' student_resid ']

#create scatterplot of predictor variable vs. studentized residuals
plt. scatter (x,y)
plt. axhline (y=0, color=' black ', linestyle=' -- ')
plt. xlabel (' Points ')
plt. ylabel (' Studentized Residuals ') 

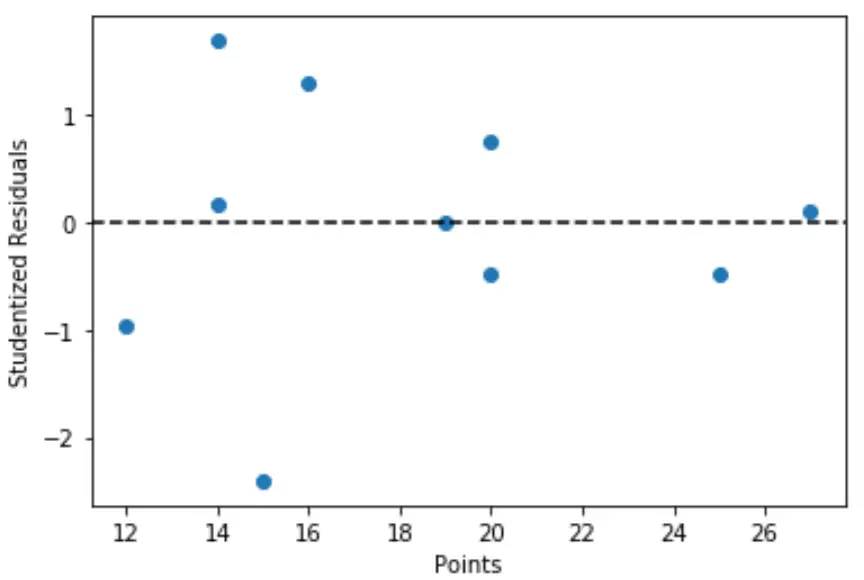
从图中我们可以看到，没有一个观测值的学生残差绝对值大于 3，因此数据集中不存在明显的异常值。

其他资源

如何在 Python 中执行简单线性回归
如何在 Python 中执行多元线性回归
如何在 Python 中创建残差图