如何在 r 中执行样条回归（带有示例）

样条回归是当数据中的模式突然变化的点或“结”并且线性回归和多项式回归不够灵活以适应数据时使用的一种回归。

以下分步示例展示了如何在 R 中执行样条回归。

第 1 步：创建数据

首先，我们在 R 中创建一个包含两个变量的数据集，并创建一个散点图来可视化变量之间的关系：

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

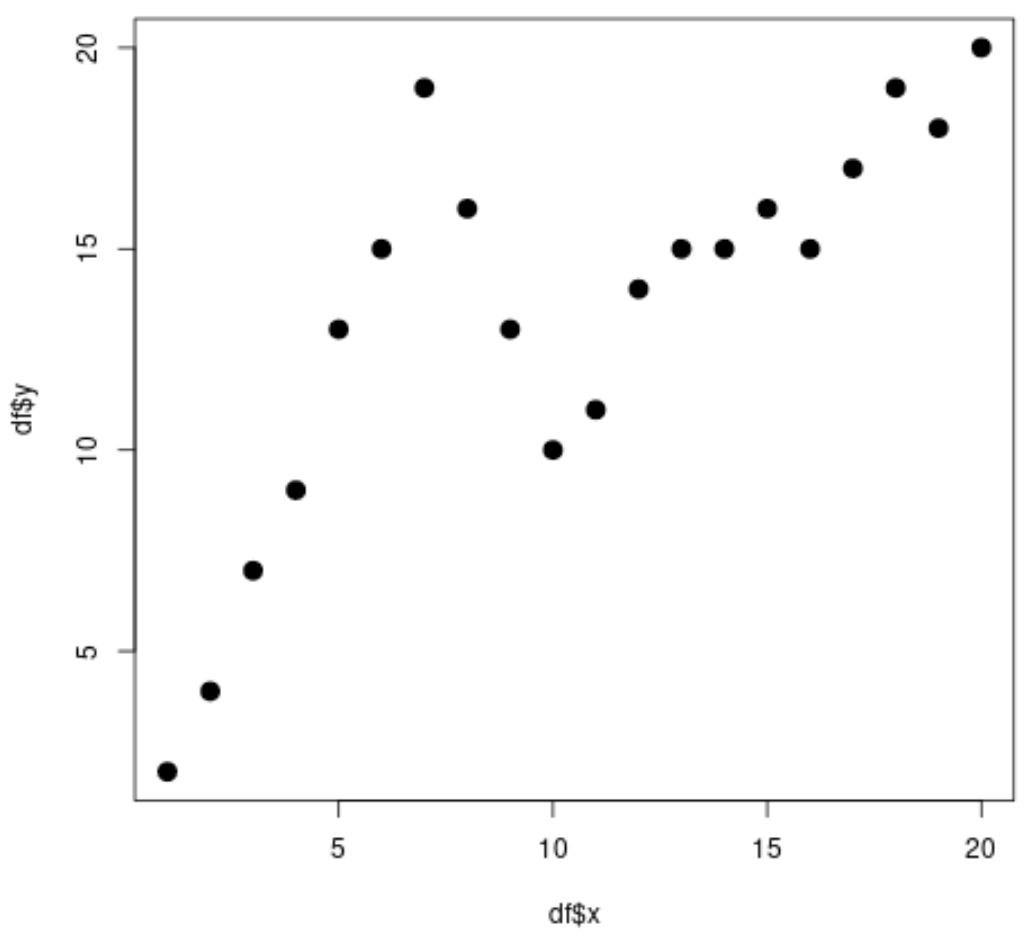
显然，x 和 y 之间的关系是非线性的，并且似乎有两个点或“节点”，数据中的模式在 x=7 和 x=10 处突然变化。

步骤 2：拟合简单线性回归模型

然后，我们使用lm() 函数对该数据集拟合一个简单的线性回归模型，并在散点图上绘制拟合回归线：

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

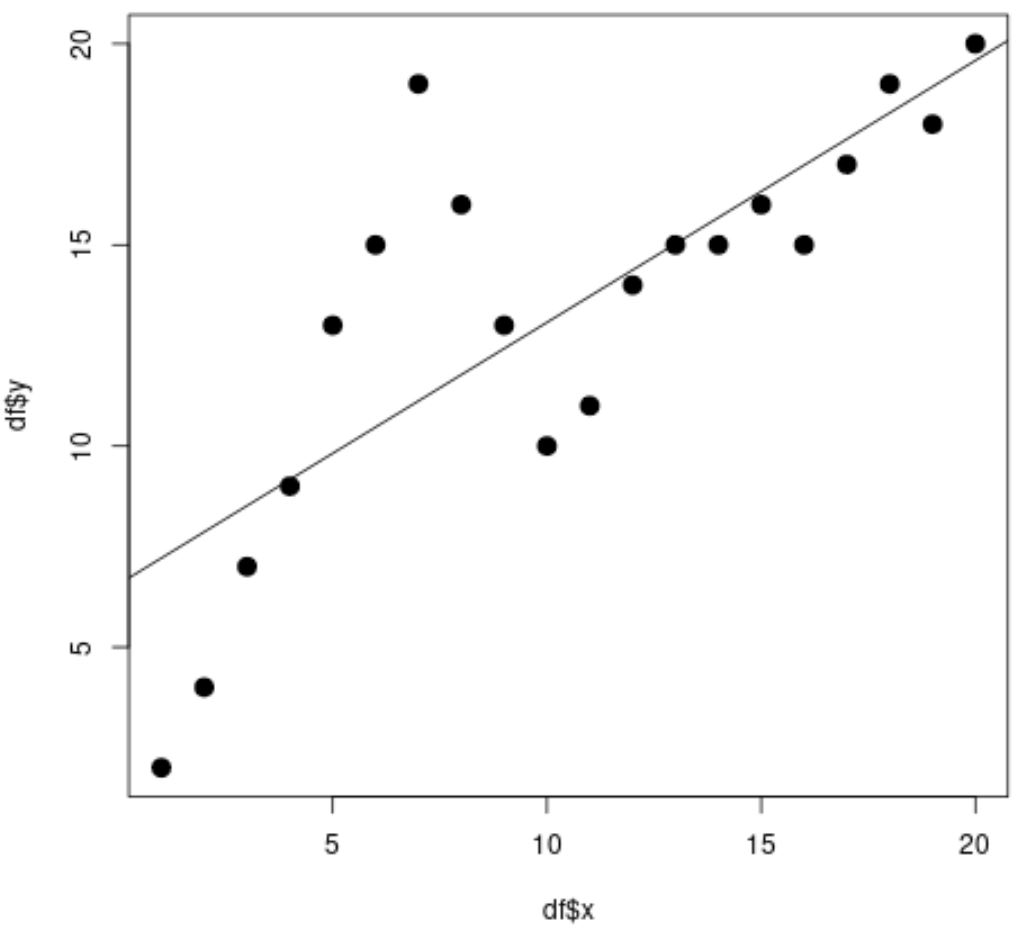
从散点图中，我们可以看到简单线性回归线不能很好地拟合数据。

从模型结果中我们还可以看到调整后的R平方值为0.5903 。

我们将其与样条模型的调整 R 平方值进行比较。

步骤 3：拟合样条回归模型

接下来，我们使用splines包中的bs()函数来拟合具有两个节点的样条回归模型，然后在散点图上绘制拟合模型：

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

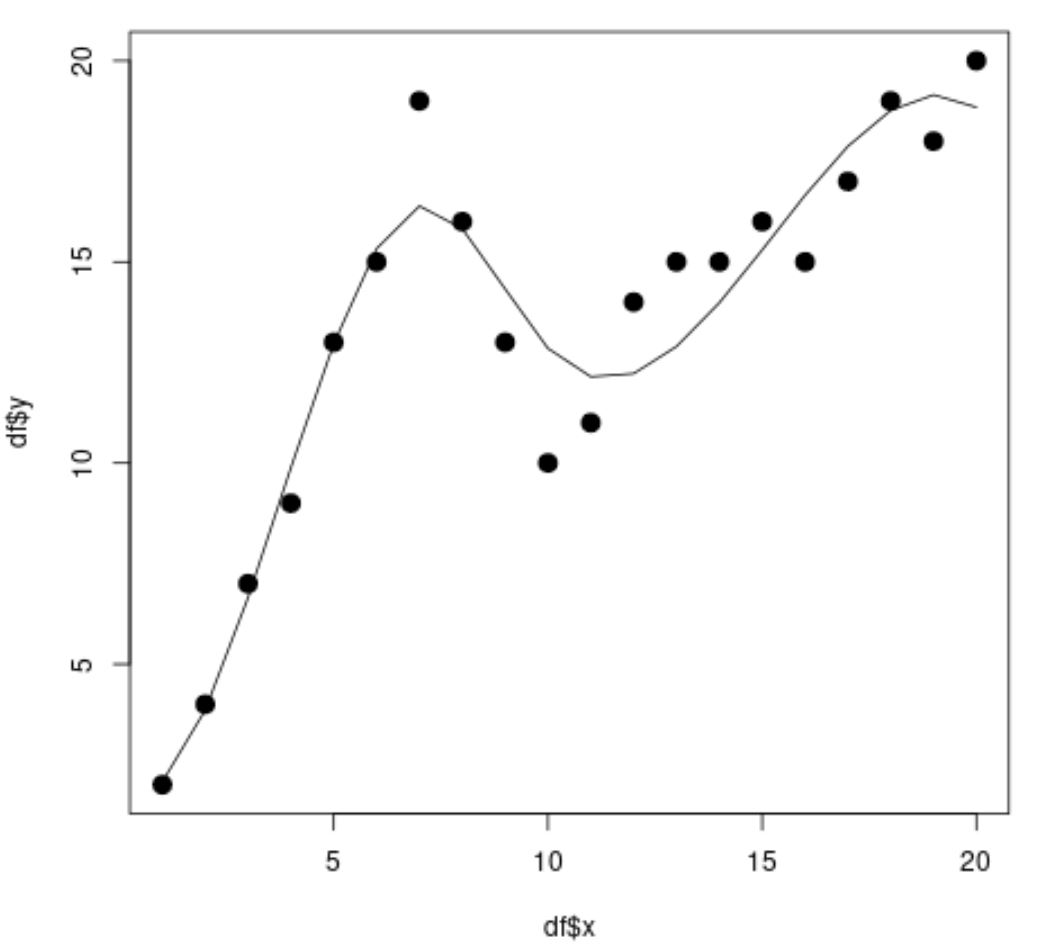
从散点图中我们可以看到样条回归模型能够很好地拟合数据。

从模型结果中我们还可以看到调整后的R平方值为0.8987 。

该模型的调整后的 R 平方值远高于简单线性回归模型，这告诉我们样条回归模型能够更好地拟合数据。

请注意，对于此示例，我们选择节点位于 x=7 和 x=10 处。

在实践中，您需要根据数据模式出现变化的位置以及您的领域专业知识自行选择节点位置。

其他资源

以下教程解释了如何在 R 中执行其他常见任务：

如何在 R 中执行多元线性回归
如何在 R 中执行指数回归
如何在 R 中执行加权最小二乘回归