如何在r中使用elbow方法寻找最优簇
机器学习中最常用的聚类算法之一称为k 均值聚类。
K 均值聚类是一种将数据集中的每个观察结果放入K个聚类中的一个技术。
最终目标是拥有K 个簇,其中每个簇内的观察结果彼此非常相似,而不同簇中的观察结果彼此非常不同。
在进行 k 均值聚类时,第一步是选择K值——我们想要将观测值放入的聚类数量。
选择K值的最常见方法之一称为肘法,该方法涉及创建一个图,其中 x 轴为簇数,y 轴为平方和总数,然后确定图中出现“膝盖”或转弯的地方。
x 轴上出现“拐点”的点告诉我们在 k 均值聚类算法中使用的最佳聚类数量。
以下示例展示了如何在 R 中使用肘部方法。
示例:在 R 中使用肘部方法
在本例中,我们将使用 R 中内置的USArrests数据集,其中包含 1973 年美国各州每 10 万人因谋杀、袭击和强奸而被捕的人数,以及每个州居住在城市的人口百分比地区。 ,城市流行音乐。
以下代码演示如何加载数据集、删除缺失值的行以及缩放数据集中的每个变量以使其平均值为 0、标准差为 1:
#load data df <-USArrests #remove rows with missing values df <- na. omitted (df) #scale each variable to have a mean of 0 and sd of 1 df <- scale(df) #view first six rows of dataset head(df) Murder Assault UrbanPop Rape Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 Arizona 0.07163341 1.4788032 0.9989801 1.042878388 Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 California 0.27826823 1.2628144 1.7589234 2.067820292 Colorado 0.02571456 0.3988593 0.8608085 1.864967207
为了找到 k-means 算法中使用的最佳簇数,我们将使用factoextra包中的fviz_nbclust()函数来创建簇数与平方和总数的关系图:
library (cluster) library (factoextra) #create plot of number of clusters vs total within sum of squares fviz_nbclust(df, kmeans, method = “ wss ”)
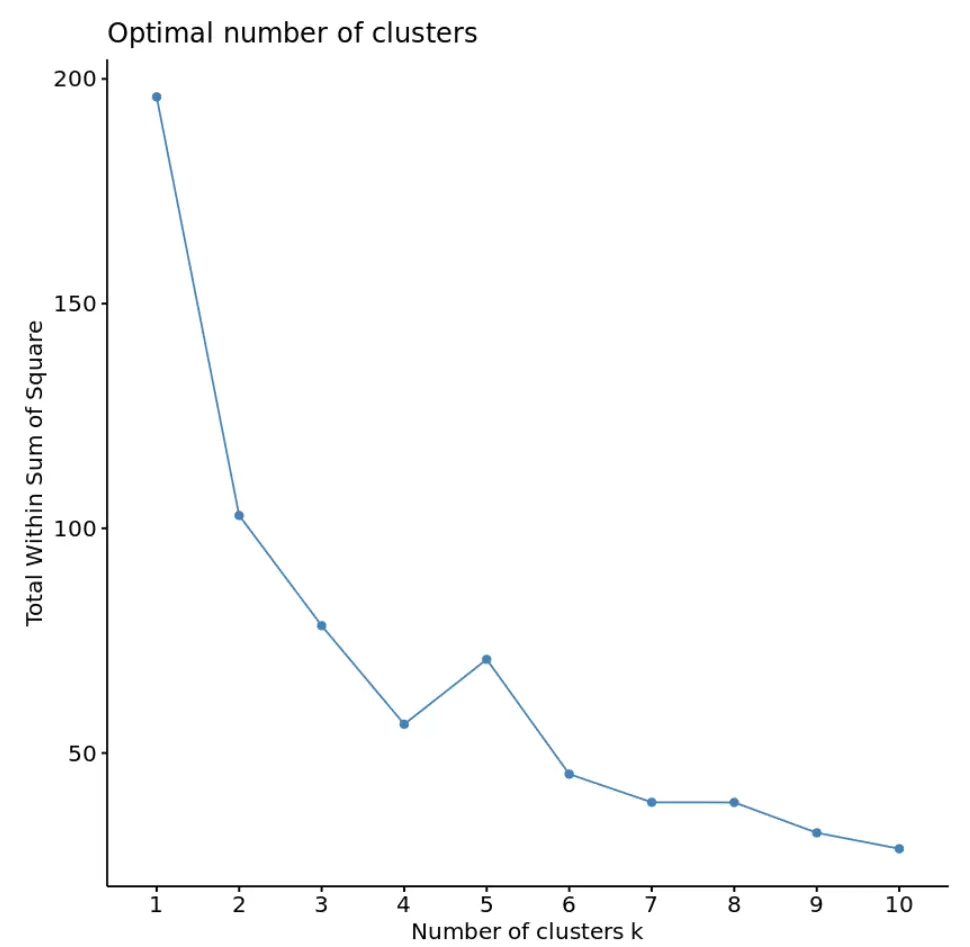
在此图中,似乎在 k = 4 个簇处存在“拐点”或扭结。这是平方和中的总数开始稳定的点。
这告诉我们 k 均值算法中使用的最佳簇数是 4。
注意:虽然通过使用更多的簇我们可能会得到更低的平方和总数,但我们可能会过度拟合训练数据,因此 k 均值算法在测试数据上效果不佳。
我们可以使用cluster包中的kmeans()函数,使用k的最佳值 4 对数据集执行 k 均值聚类:
#make this example reproducible set. seeds (1) #perform k-means clustering with k = 4 clusters km <- kmeans(df, centers = 4, nstart = 25) #view results km K-means clustering with 4 clusters of sizes 16, 13, 13, 8 Cluster means: Murder Assault UrbanPop Rape 1 -0.4894375 -0.3826001 0.5758298 -0.26165379 2 -0.9615407 -1.1066010 -0.9301069 -0.96676331 3 0.6950701 1.0394414 0.7226370 1.27693964 4 1.4118898 0.8743346 -0.8145211 0.01927104 Vector clustering: Alabama Alaska Arizona Arkansas California Colorado 4 3 3 4 3 3 Connecticut Delaware Florida Georgia Hawaii Idaho 1 1 3 4 1 2 Illinois Indiana Iowa Kansas Kentucky Louisiana 3 1 2 1 2 4 Maine Maryland Massachusetts Michigan Minnesota Mississippi 2 3 1 3 2 4 Missouri Montana Nebraska Nevada New Hampshire New Jersey 3 2 2 3 2 1 New Mexico New York North Carolina North Dakota Ohio Oklahoma 3 3 4 2 1 1 Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 1 1 1 4 2 4 Texas Utah Vermont Virginia Washington West Virginia 3 1 2 1 1 2 Wisconsin Wyoming 2 1 Within cluster sum of squares by cluster: [1] 16.212213 11.952463 19.922437 8.316061 (between_SS / total_SS = 71.2%) Available components: [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" [7] "size" "iter" "ifault"
从结果我们可以看出:
- 16 个州被分配到第一个集群
- 13个州已被分配到第二个集群
- 13个州已被分配到第三集群
- 8个州已被分配到第四集群
我们还可以将每个状态的聚类分配添加到原始数据集中:
#add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)
#view final data
head(final_data)
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2
原始数据库中的每个观察结果都被分为四组之一。
其他资源
以下教程提供了有关如何在 R 中运行各种聚类算法的分步示例:
R 中的 K 均值聚类:分步示例
R 中的 K-Medoids 聚类:分步示例
R 中的层次聚类:分步示例