如何在 r 中执行分位数回归

线性回归是一种我们可以用来理解一个或多个预测变量与响应变量之间关系的方法。

通常，当我们执行线性回归时，我们想要估计响应变量的平均值。

但是，我们可以使用一种称为分位数回归的方法来估计响应值的任何分位数或百分位数，例如第 70 个百分位数、第 90 个百分位数、第 98 个百分位数等。

要在 R 中执行分位数回归，我们可以使用quantreg包中的rq()函数，该函数使用以下语法：

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

金子：

• y：响应变量
• x：预测变量
• data：数据集的名称
• tau：要查找的百分位数。默认值为中位数 (tau = 0.5)，但您可以将其设置为 0 到 1 之间的任何数字。

本教程提供了如何使用此函数在 R 中执行分位数回归的分步示例。

第 1 步：输入数据

在此示例中，我们将创建一个数据集，其中包含大学 100 名不同学生的学习时间和考试成绩：

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

第 2 步：执行分位数回归

接下来，我们将使用学习时间作为预测变量和考试成绩作为响应变量来拟合分位数回归模型。

我们将使用该模型根据学习小时数来预测预期的 90% 考试成绩：

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

从结果中我们可以看到估计的回归方程：

90% 考试成绩 = 60.25 + 2.437*（小时）

例如，所有学习 8 小时的学生的第 90 个百分位数分数应为 79.75：

考试成绩的第 90 个百分位数 = 60.25 + 2.437*(8) = 79.75 。

输出还显示预测变量的截距和时间的置信上限和下限。

第 3 步：可视化结果

我们还可以通过创建散点图来可视化回归结果，并将拟合的分位数回归方程叠加在图表上：

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

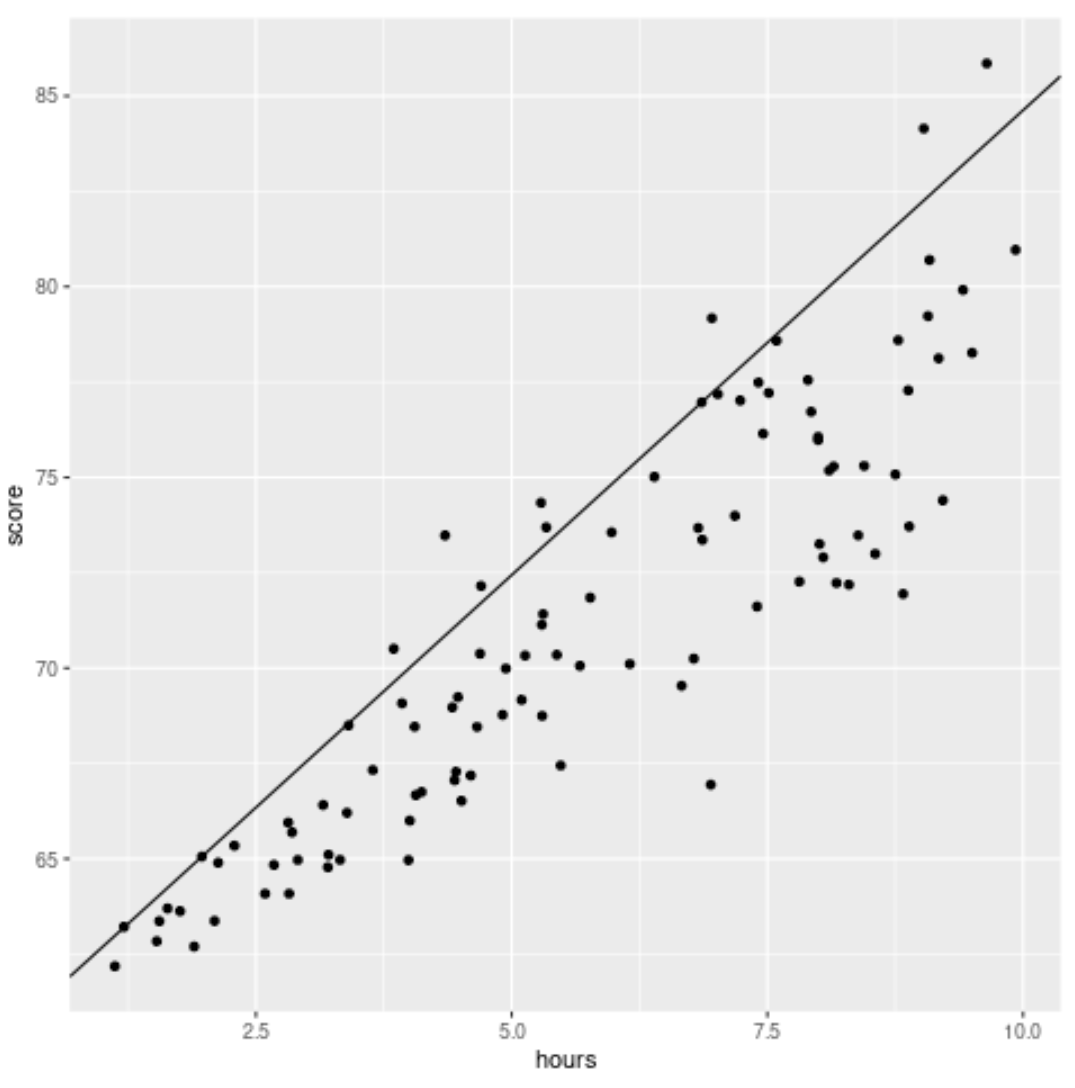
与传统的线性回归线不同，请注意，这条拟合线不会穿过数据的核心。相反，它会通过预测变量每个水平的估计第 90 个百分位。

通过添加geom_smooth()参数，我们可以看到拟合分位数回归方程和简单线性回归方程之间的差异：

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

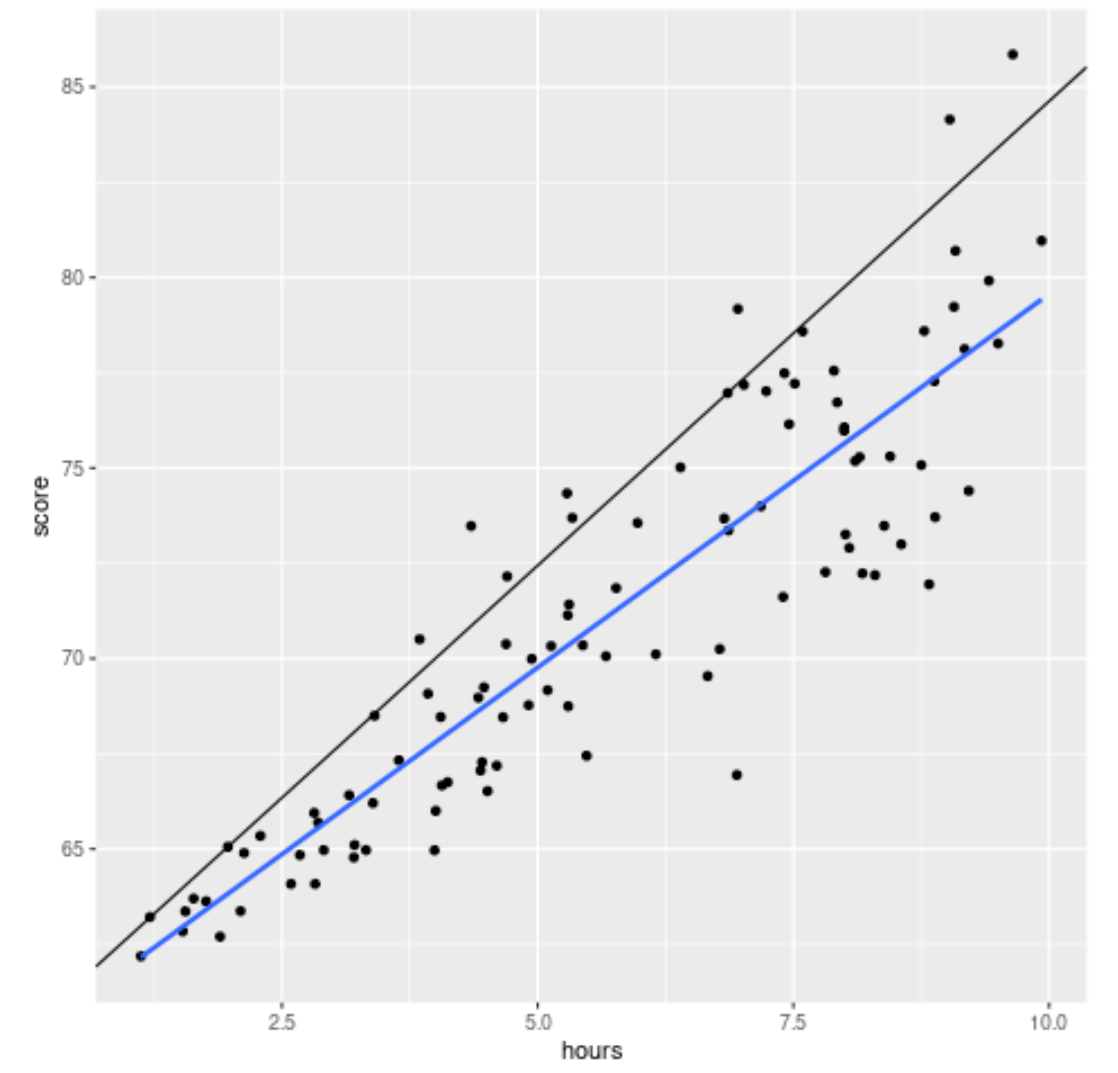
黑线显示针对第 90 个百分位数调整的分位数回归线，蓝线显示简单线性回归线，用于估计响应变量的平均值。

正如预期的那样，简单线性回归线贯穿数据并向我们显示每个小时级别的考试成绩的估计平均值。

其他资源

以下教程解释了如何在 R 中执行其他常见任务：

如何在 R 中执行简单线性回归
如何在 R 中执行多元线性回归
如何在 R 中执行二次回归