如何在 r 中创建部分残差图
多元线性回归是一种统计方法,我们可以用它来理解多个预测变量和响应变量之间的关系。
然而,多元线性回归的关键假设之一是每个预测变量和响应变量之间存在线性关系。
如果不满足这个假设,那么回归模型的结果可能不可靠。
测试此假设的一种方法是创建部分残差图,该图显示预测变量相对于响应变量的残差。
以下示例演示如何在 R 中为回归模型创建部分残差图。
示例:如何在 R 中创建部分残差图
假设我们在 R 中拟合一个具有三个预测变量的回归模型:
#make this example reproducible set. seeds (0) #define response variable y <- c(1:1000) #define three predictor variables x1 <- c(1:1000)*runif(n=1000) x2 <- (c(1:1000)*rnorm(n=1000))^2 x3 <- (c(1:1000)*rnorm(n=1000))^3 #fit multiple linear regression model model <- lm(y~x1+x2+x3))
我们可以使用 R 中car包中的crPlots()函数为模型中的每个预测变量创建部分残差图:
library (car) #create partial residual plots crPlots(model)
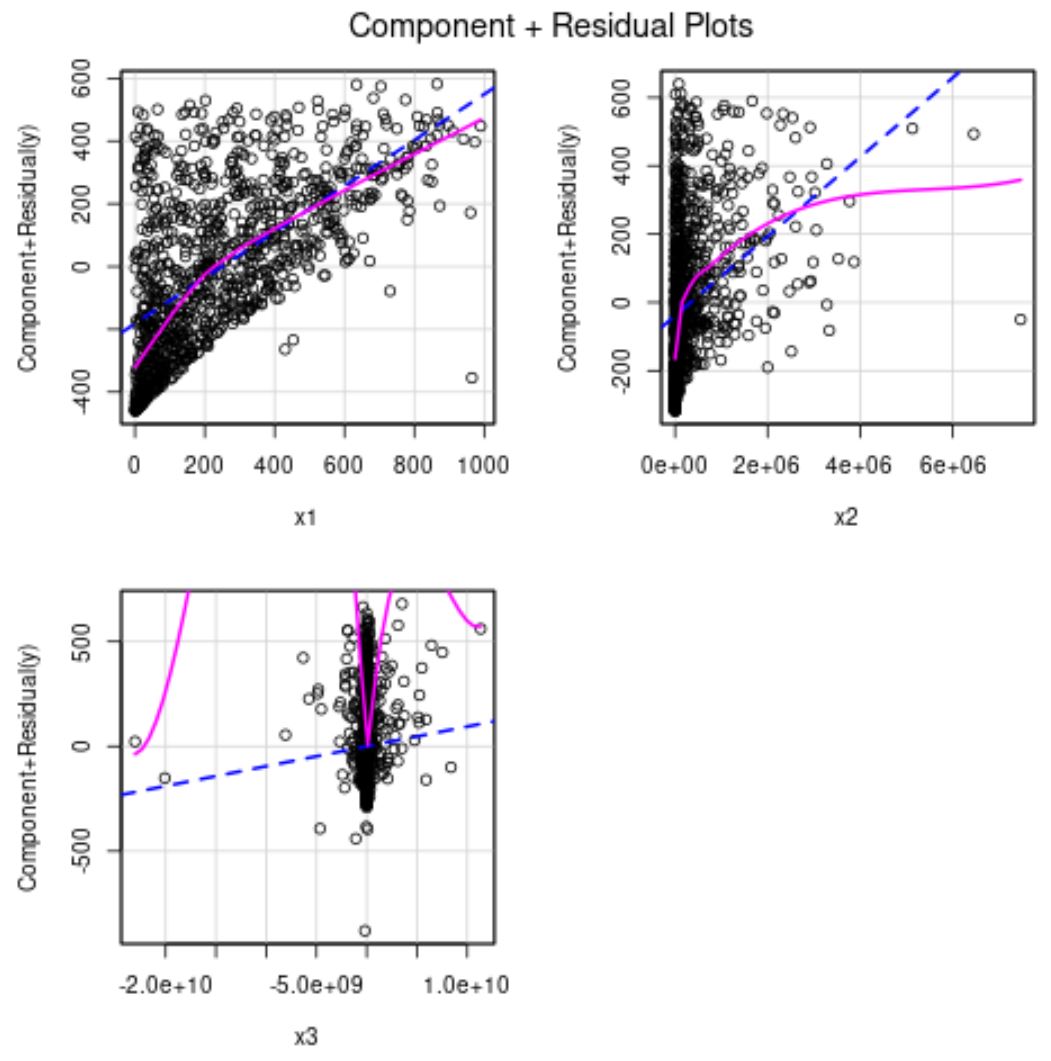
如果预测变量和响应变量之间的关系是线性的,蓝线显示预期残差。粉色线显示实际残差。
如果两条线显着不同,则表明存在非线性关系。
从上图中我们可以看到 x2 和 x3 的残差呈现非线性。
这违反了多元线性回归的线性假设。解决此问题的一种方法是对预测变量使用平方根或立方根变换:
library (car) #fit new model with transformed predictor variables model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3))) #create partial residual plots for new model crPlots(model_transformed)
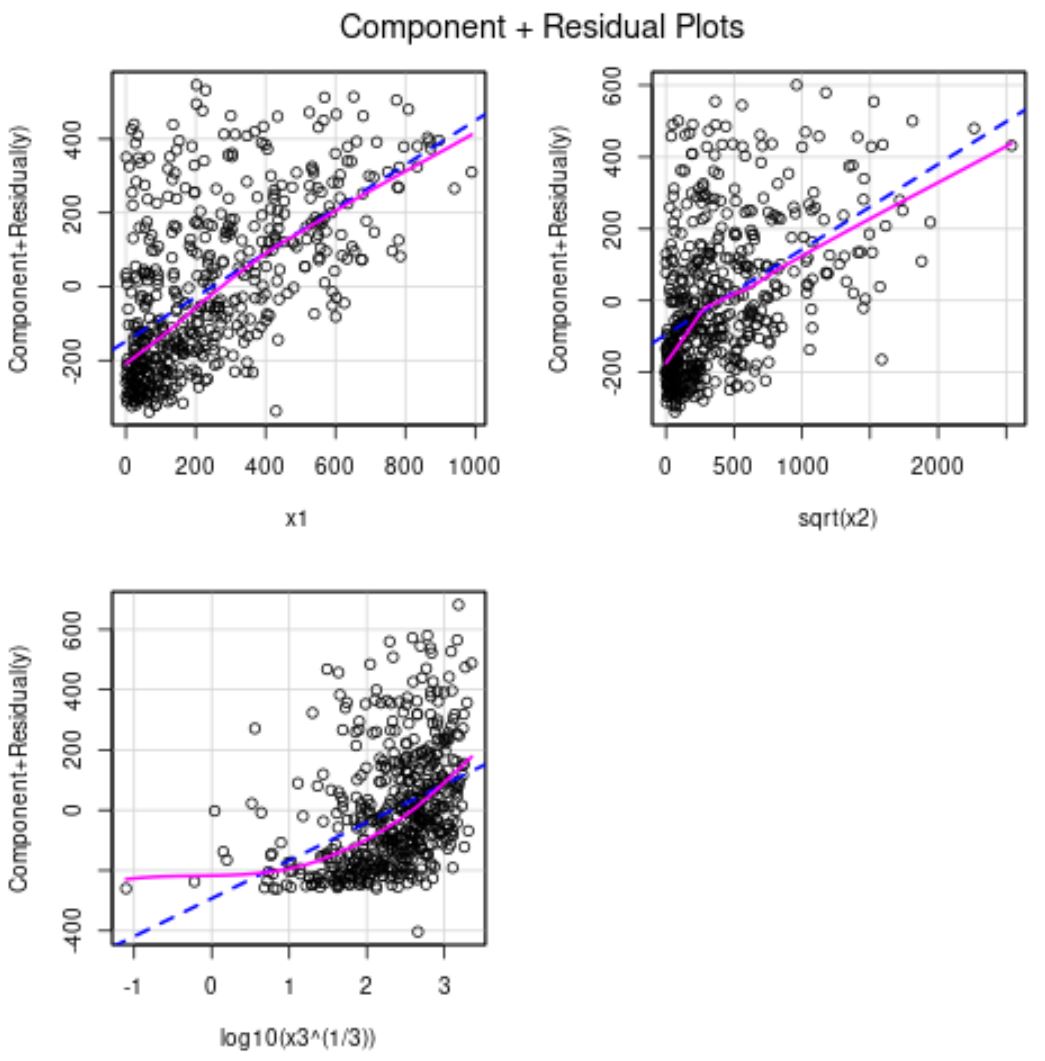
从部分残差图中,我们可以看到 x2 现在与响应变量具有更加线性的关系。
x3 预测变量仍然有些非线性,因此我们可能决定尝试另一种转换,或者可能从模型中完全删除该变量。
其他资源
以下教程解释了如何在 R 中创建其他常见绘图: