如何在 r 中执行加权最小二乘回归
线性回归的关键假设之一是残差在预测变量的每个水平上以相等方差分布。这种假设称为同方差性。
如果不遵守此假设,则称残差中存在异方差性。当这种情况发生时,回归结果变得不可靠。
解决此问题的一种方法是使用加权最小二乘回归,它为观测值分配权重,使得误差方差较小的观测值获得更多权重,因为与误差方差较大的观测值相比,它们包含更多信息。
本教程提供了如何在 R 中执行加权最小二乘回归的分步示例。
第 1 步:创建数据
以下代码创建一个数据框,其中包含 16 名学生的学习小时数和相应的考试成绩:
df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))
第 2 步:执行线性回归
接下来,我们将使用lm()函数来拟合一个简单的线性回归模型,该模型使用小时作为预测变量,得分作为响应变量:
#fit simple linear regression model model <- lm(score ~ hours, data = df) #view summary of model summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -17,967 -5,970 -0.719 7,531 15,032 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 60,467 5,128 11,791 1.17e-08 *** hours 5,500 1,127 4,879 0.000244 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 9.224 on 14 degrees of freedom Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438
步骤 3:检验异方差性
接下来,我们将创建残差和拟合值的图,以直观地检查异方差性:
#create residual vs. fitted plot plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ') #add a horizontal line at 0 abline(0,0)
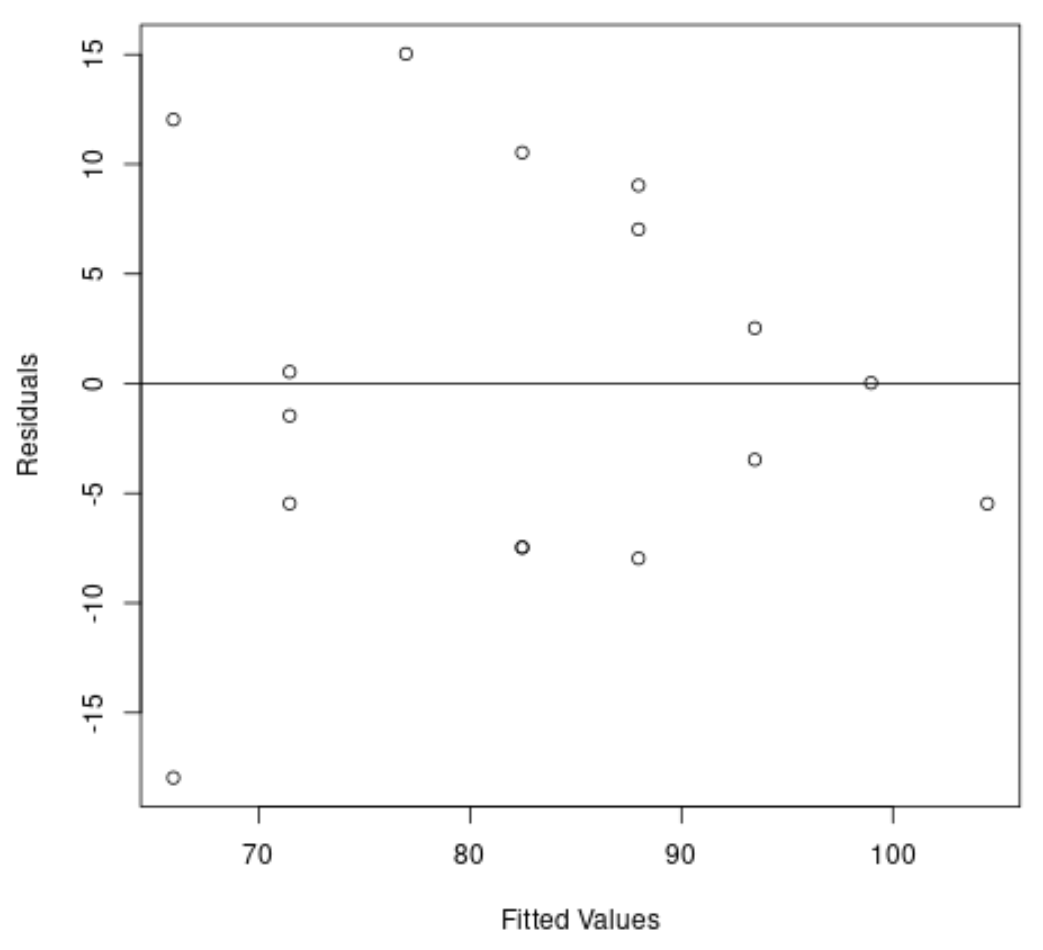
从图中我们可以看出,残差呈“圆锥”形状:它们在整个图中的方差分布并不均匀。
为了正式测试异方差性,我们可以执行 Breusch-Pagan 测试:
#load lmtest package library (lmtest) #perform Breusch-Pagan test bptest(model) studentized Breusch-Pagan test data: model BP = 3.9597, df = 1, p-value = 0.0466
Breusch-Pagan 检验使用以下原假设和备择假设:
- 零假设 (H 0 ):存在同方差性(残差以等方差分布)
- 备择假设 ( HA ):存在异方差性(残差不以等方差分布)
由于检验的 p 值为0.0466 ,我们将拒绝原假设并得出异方差是该模型中的问题的结论。
步骤 4:执行加权最小二乘回归
由于存在异方差性,我们将通过设置权重来执行加权最小二乘法,以使方差较低的观测值获得更多的权重:
#define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2
#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)
#view summary of model
summary(wls_model)
Call:
lm(formula = score ~ hours, data = df, weights = wt)
Weighted Residuals:
Min 1Q Median 3Q Max
-2.0167 -0.9263 -0.2589 0.9873 1.6977
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05
从结果中我们可以看到,小时预测变量的系数估计值略有变化,整体模型拟合度有所改善。
加权最小二乘模型的残差标准误差为1.199 ,而原始简单线性回归模型的残差标准误差为9.224 。
这表明与简单线性回归模型产生的预测值相比,加权最小二乘模型产生的预测值更接近实际观测值。
加权最小二乘模型的 R 平方也为0.6762 ,而原始简单线性回归模型中的 R 平方为0.6296 。
这表明加权最小二乘模型比简单线性回归模型能够解释更多的考试成绩方差。
这些测量结果表明,与简单线性回归模型相比,加权最小二乘模型可以更好地拟合数据。