R 中的 brown–forsythe 测试:分步示例
单向方差分析用于确定三个或更多独立组的平均值之间是否存在显着差异。
测试这一点的最常见方法之一是使用Brown-Forsythe 测试,这是一种使用以下假设的统计测试:
- H 0 :总体之间的方差相等。
- H A :人群之间的差异并不相等。
如果检验的p 值低于一定的显着性水平(例如 α = 0.05),则我们拒绝零假设并得出结论:不同总体之间的方差不相等。
本教程提供了如何在 R 中执行 Brown-Forsythe 测试的分步示例。
第 1 步:输入数据
假设我们想知道三种不同的锻炼计划是否会导致不同程度的减肥。
为了测试这一点,我们招募了 90 人,并随机分配 30 人使用每个程序。然后我们在一个月后测量每个人的体重减轻情况。
以下数据集包含有关每个计划的减重量信息:
#make this example reproducible set.seed(0) #create data frame data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)), weight_loss = c( runif (30, 0, 3), runif (30, 0, 5), runif (30, 1, 7))) #view first six rows of data frame head(data) # program weight_loss #1 A 2.6900916 #2 A 0.7965260 #3 A 1.1163717 #4 A 1.7185601 #5 A 2.7246234 #6 A 0.6050458
第 2 步:总结并可视化数据
在执行 Brown-Forsythe 检验之前,我们可以创建箱线图来可视化每组体重减轻的方差:
boxplot(weight_loss ~ program, data = data)
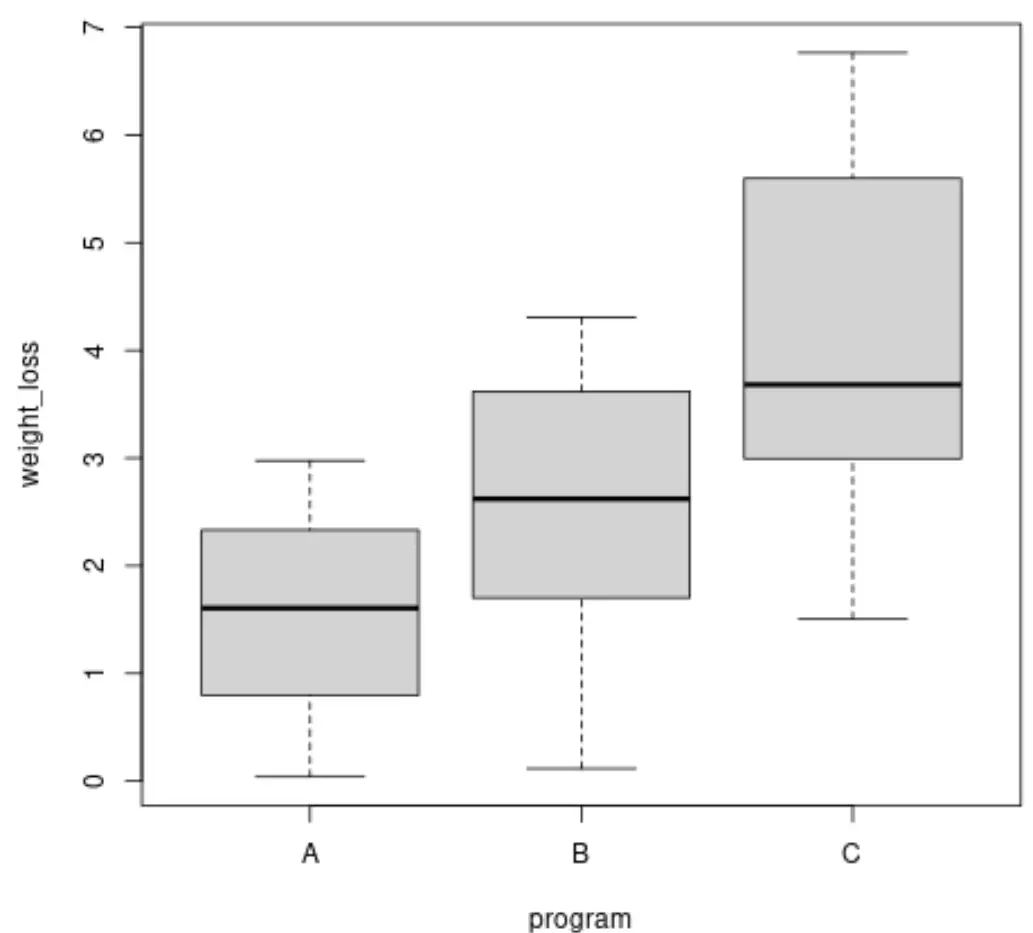
我们还可以计算每组体重减轻的方差:
#load dplyr package library (dplyr) #calculate variance of weight loss by group data %>% group_by (program) %>% summarize (var=var(weight_loss)) # A tibble: 3 x 2 program var 1 A 0.819 2 B 1.53 3 C 2.46
我们可以看到组之间的方差不同,但要确定这些差异是否具有统计显着性,我们可以执行 Brown-Forsythe 检验。
第 3 步:执行 Brown-Forsythe 测试
要在 R 中执行 Brown-Forsythe 测试,我们可以使用onewaytests包中的bf.test()函数:
#load onewaytests package library (onewaytests) #perform Brown-Forsythe test bf.test(weight_loss ~ program, data = data) Brown-Forsythe Test (alpha = 0.05) -------------------------------------------------- ----------- data: weight_loss and program statistic: 30.83304 num df: 2 name df: 74.0272 p.value: 1.816529e-10 Result: Difference is statistically significant. -------------------------------------------------- -----------
检验的 p 值小于 0.000,结果表明,三组之间的方差差异具有统计显着性。
下一步
如果您无法拒绝 Brown-Forsythe 检验的原假设,则可以对数据执行单向方差分析。
但是,如果拒绝原假设,则意味着违反了方差齐性假设。在这种情况下,您有两种选择:
1. 无论如何都要进行单向方差分析。
事实证明,只要最大方差不大于最小方差的 4 倍,单向方差分析实际上对不等方差具有鲁棒性。
在上例的第 2 步中,我们发现最小方差为 0.819,最大方差为 2.46。因此最大方差与最小方差之比为 2.46 / 0.819 = 3.003 。
由于该值小于 4,我们可以简单地进行单向方差分析。
2. 执行 Kruskal-Wallis 测试
如果最大方差与最小方差之比大于 4,则可以选择执行Kruskal-Wallis 检验。这被认为是单向方差分析的非参数等价物。
您可以在此处找到 R 中 Kruskal-Wallis 测试的分步示例。