如何在 r 中测试正态性(4 种方法)
许多统计测试假设数据集呈正态分布。
在 R 中检查此假设有四种常见方法:
1.(可视化方法)创建直方图。
- 如果直方图近似为“钟形”形状,则假定数据呈正态分布。
2.(可视化方法)创建QQ图。
- 如果图上的点大致沿直线对角线分布,则假定数据呈正态分布。
3.(正式统计检验)执行 Shapiro-Wilk 检验。
- 如果检验的 p 值大于 α = 0.05,则假定数据呈正态分布。
4.(正式统计检验)执行 Kolmogorov-Smirnov 检验。
- 如果检验的 p 值大于 α = 0.05,则假定数据呈正态分布。
以下示例展示了如何在实践中使用每种方法。
方法 1:创建直方图
以下代码展示了如何在 R 中为正态分布和非正态分布数据集创建直方图:
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#define plotting region
by(mfrow=c(1,2))
#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ')
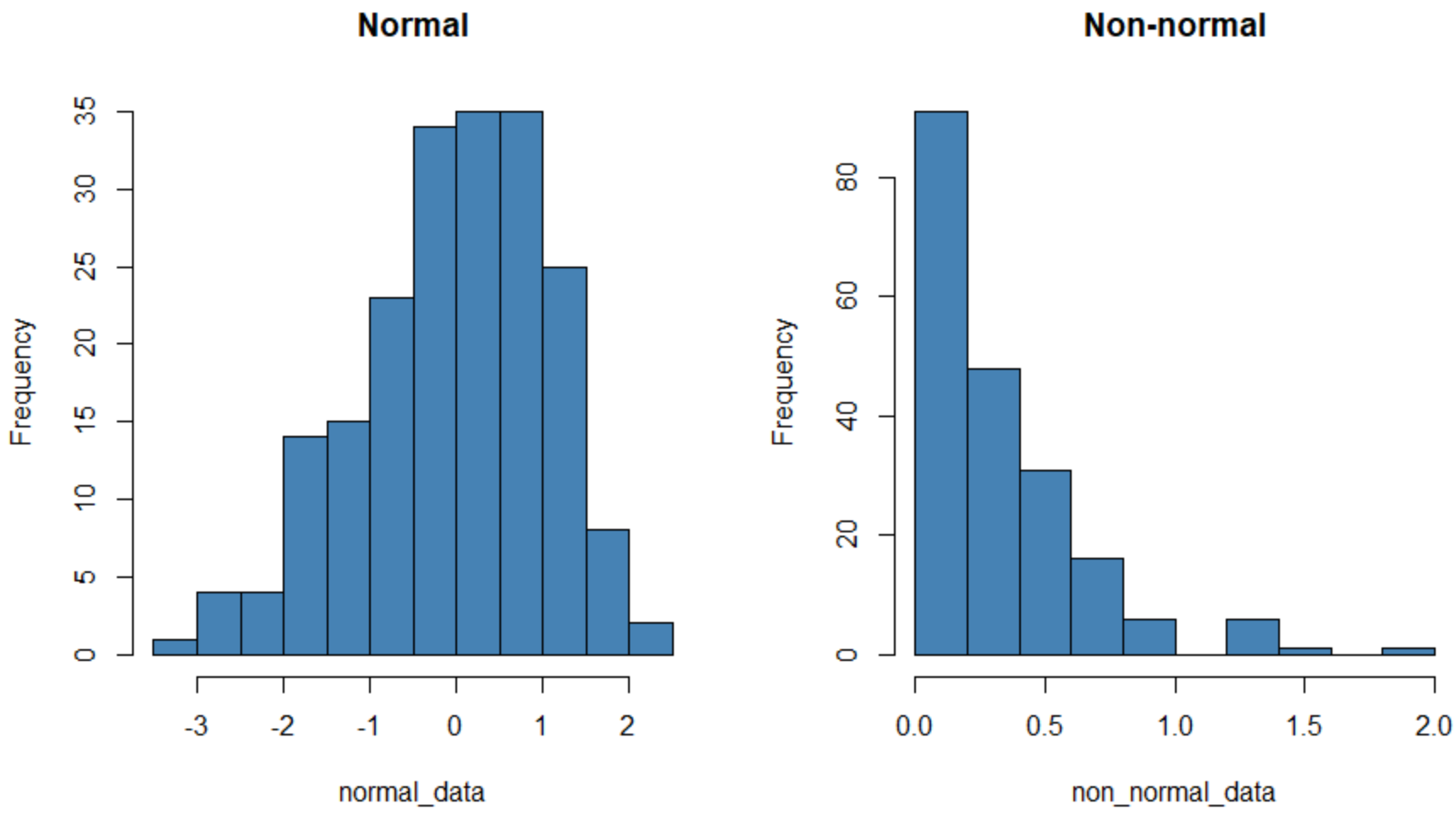
左侧的直方图显示了正态分布的数据集(大致“钟形”形状),右侧的直方图显示了非正态分布的数据集。
方法2:创建QQ图
以下代码展示了如何在 R 中为正态分布和非正态分布数据集创建 QQ 图:
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#define plotting region
by(mfrow=c(1,2))
#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)
qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)
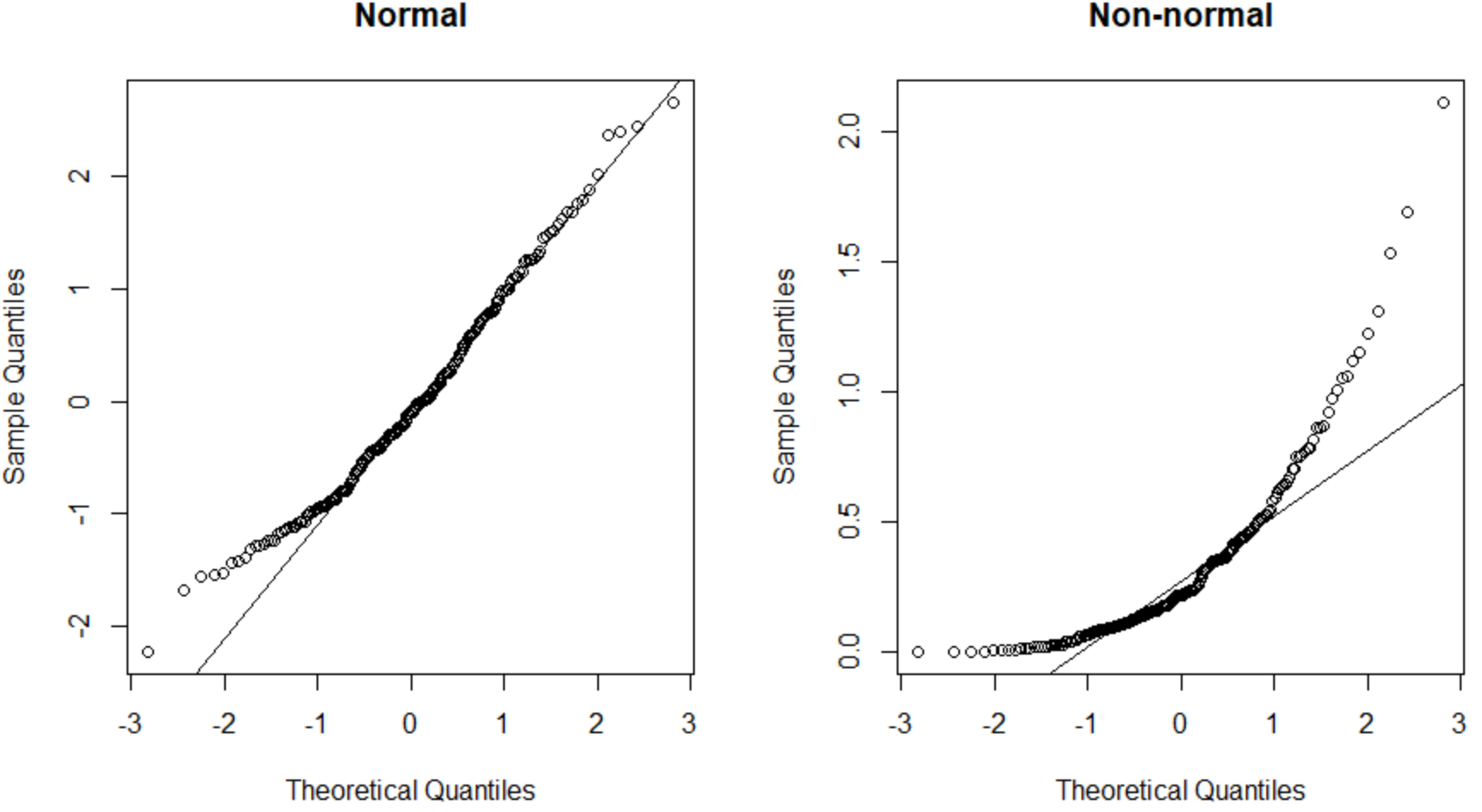
左侧的 QQ 图呈现正态分布的数据集(点沿直线对角线分布),右侧的 QQ 图呈现非正态分布的数据集。
方法 3:执行 Shapiro-Wilk 检验
以下代码显示如何在 R 中对正态分布和非正态分布数据集执行 Shapiro-Wilk 检验:
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#perform shapiro-wilk test
shapiro. test (normal_data)
Shapiro-Wilk normality test
data: normal_data
W = 0.99248, p-value = 0.3952
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#perform shapiro-wilk test
shapiro. test (non_normal_data)
Shapiro-Wilk normality test
data: non_normal_data
W = 0.84153, p-value = 1.698e-13
第一次检验的 p 值不小于 0.05,这表明数据呈正态分布。
第二次检验的 p 值小于0.05,表明数据不呈正态分布。
方法 4:执行 Kolmogorov-Smirnov 检验
以下代码展示了如何在 R 中对正态分布和非正态分布数据集执行 Kolmogorov-Smirnov 检验:
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')
One-sample Kolmogorov–Smirnov test
data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ')
One-sample Kolmogorov–Smirnov test
data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided
第一次检验的 p 值不小于 0.05,这表明数据呈正态分布。
第二次检验的 p 值小于0.05,表明数据不呈正态分布。
如何处理非正态数据
如果给定的数据集不是正态分布的,我们通常可以执行以下转换之一以使其更加正态分布:
1. 对数变换:将x值变换为log(x) 。
2. 平方根变换:将x的值变换为√x 。
3.立方根变换:将x的值变换为x 1/3 。
通过执行这些转换,数据集通常变得更加正态分布。
阅读 本教程以了解如何在 R 中执行这些转换。
其他资源
如何在 R 中创建直方图
如何在 R 中创建和解释 QQ 图
如何在 R 中执行 Shapiro-Wilk 检验
如何在 R 中执行 Kolmogorov-Smirnov 检验