如何计算 r 中的 phi 系数
Phi 系数(有时称为均方列联系数)是两个二元变量之间关联性的度量。
对于给定两个随机变量x和y的 2×2 表:

Phi系数可以计算如下:
Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)
示例:计算 R 中的 Phi 系数
假设我们想知道性别是否与对政党的偏好相关。因此,我们对 25 名选民进行了简单的随机抽样,并询问他们对政党的偏好。
下表列出了调查结果:
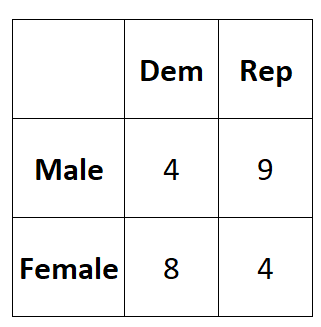
我们可以使用以下代码将这些数据输入到 R 中的 2×2 矩阵中:
#create 2x2 table data = matrix(c(4, 8, 9, 4), nrow = 2 ) #view dataset data [,1] [,2] [1,] 4 9 [2,] 8 4
然后我们可以使用psych包中的phi()函数来计算两个变量之间的 Phi 系数:
#load psych package library (psych) #calculate Phi Coefficient phi(data) [1] -0.36
Phi 系数结果为-0.36 。
请注意,phi 函数默认四舍五入为 2 位数字,但您可以指定该函数四舍五入为所需的任意位数:
#calculate Phi Coefficient and round to 6 digits phi(data, digits = 6 ) [1] -0.358974
如何解释 Phi 系数
与 Pearson 相关系数类似,Phi 系数取 -1 到 1 之间的值,其中:
- -1表示两个变量之间完全负相关。
- 0表示两个变量之间没有关联。
- 1表明两个变量之间存在完全正相关关系。
一般来说,Phi 系数离零越远,两个变量之间的关系越强。
换句话说,Phi 系数离零越远,两个变量之间存在某种系统模式的证据就越多。
其他资源
Phi系数简介
Phi系数计算器