R 中的主成分回归(逐步)
给定一组p个预测变量和一个响应变量,多元线性回归使用最小二乘法来最小化残差平方和 (RSS):
RSS = Σ(y i – ŷ i ) 2
金子:
- Σ :希腊符号,意思是和
- y i :第 i 个观测值的实际响应值
- ŷ i :基于多元线性回归模型的预测响应值
然而,当预测变量高度相关时, 多重共线性可能会成为一个问题。这可能会使模型系数估计不可靠并表现出较高的方差。
避免此问题的一种方法是使用主成分回归,它找到原始p个预测变量的M 个线性组合(称为“主成分”),然后使用最小二乘法来拟合使用主成分作为预测变量的线性回归模型。
本教程提供了如何在 R 中执行主成分回归的分步示例。
第1步:加载必要的包
在 R 中执行主成分回归的最简单方法是使用pls包中的函数。
#install pls package (if not already installed) install.packages(" pls ") load pls package library(pls)
步骤2:调整PCR模型
在此示例中,我们将使用名为mtcars的内置 R 数据集,其中包含不同类型汽车的数据:
#view first six rows of mtcars dataset
head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1
对于此示例,我们将使用hp作为响应变量并使用以下变量作为预测变量来拟合主成分回归 (PCR) 模型:
- 英里/加仑
- 展示
- 拉屎
- 重量
- 快秒
以下代码显示了如何使 PCR 模型适合此数据。请注意以下参数:
- scale=TRUE :这告诉 R 每个预测变量都应该缩放为均值 0 和标准差 1。这确保如果以不同单位进行测量,则预测变量不会对模型产生太大影响。 。
- validation=”CV” :这告诉 R 使用k 折交叉验证来评估模型性能。请注意,默认情况下使用 k=10 折叠。另请注意,您可以指定“LOOCV”来代替执行留一交叉验证。
#make this example reproducible set.seed(1) #fit PCR model model <- pcr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")
第三步:选择主要部件的数量
一旦我们调整了模型,我们需要确定有多少主成分值得保留。
为此,只需查看通过 k 交叉验证计算出的测试均方根误差(测试 RMSE):
#view summary of model fitting
summary(model)
Data:
Y dimension: 32 1
Fit method: svdpc
Number of components considered: 5
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 44.56 35.64 35.83 36.23 36.67
adjCV 69.66 44.44 35.27 35.43 35.80 36.20
TRAINING: % variance explained
1 comp 2 comps 3 comps 4 comps 5 comps
X 69.83 89.35 95.88 98.96 100.00
hp 62.38 81.31 81.96 81.98 82.03
结果中有两个有趣的表:
1. 验证:RMSEP
该表告诉我们通过 k 倍交叉验证计算出的 RMSE 检验。我们可以看到以下内容:
- 如果我们在模型中仅使用原始项,则检验的 RMSE 为69.66 。
- 如果我们添加第一个主成分,RMSE 测试将降至44.56。
- 如果我们添加第二个主成分,RMSE 测试将降至35.64。
我们可以看到,添加额外的主成分实际上会导致测试的 RMSE 增加。因此,看来在最终模型中仅使用两个主成分是最佳的。
2. 训练:解释方差百分比
该表告诉我们由主成分解释的响应变量的方差百分比。我们可以看到以下内容:
- 仅使用第一个主成分,我们可以解释响应变量中69.83%的变异。
- 通过添加第二个主成分,我们可以解释响应变量中89.35%的变异。
请注意,我们仍然可以通过使用更多的主成分来解释更多的方差,但是我们可以看到,添加两个以上的主成分实际上并不会增加解释方差的百分比太多。
我们还可以使用validationplot()函数将RMSE检验(以及MSE和R平方检验)可视化为主成分数量的函数。
#visualize cross-validation plots
validationplot(model)
validationplot(model, val.type="MSEP")
validationplot(model, val.type="R2")
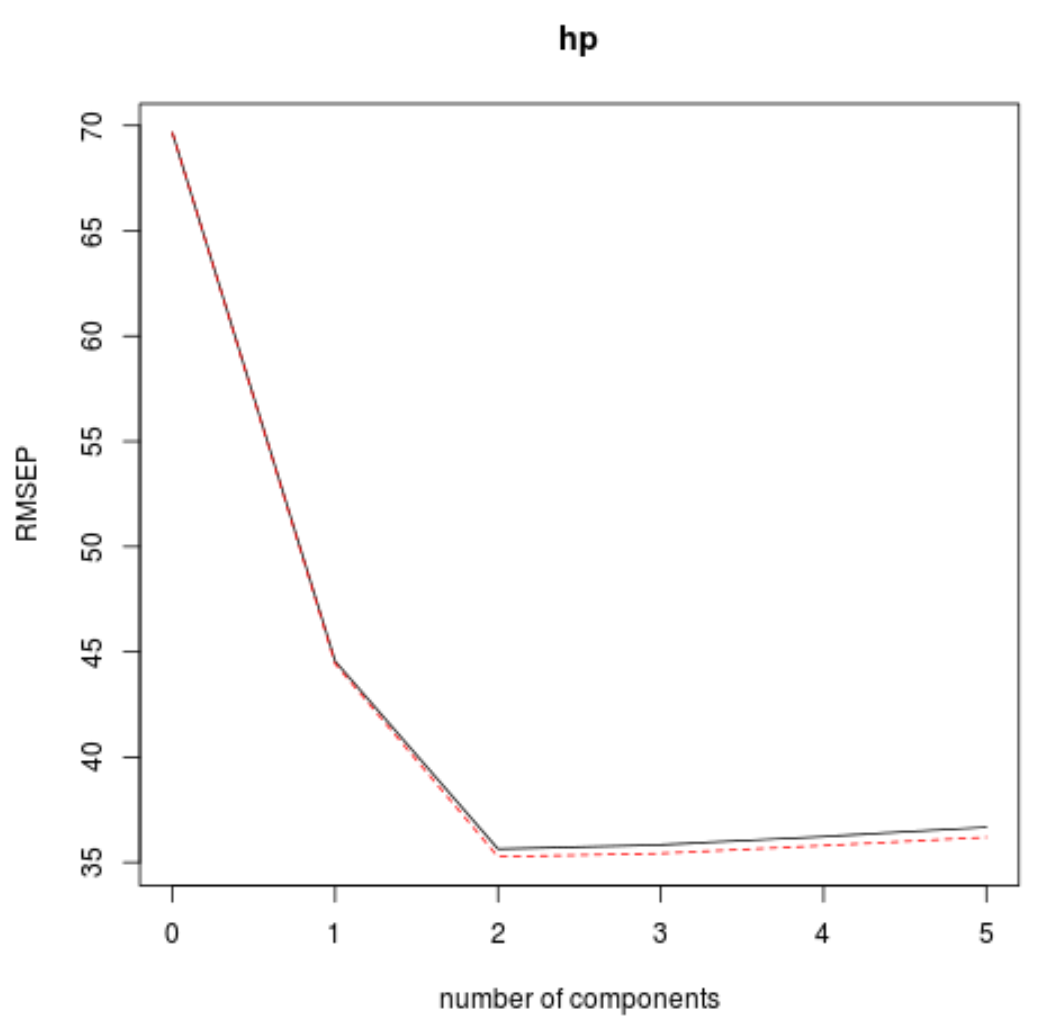
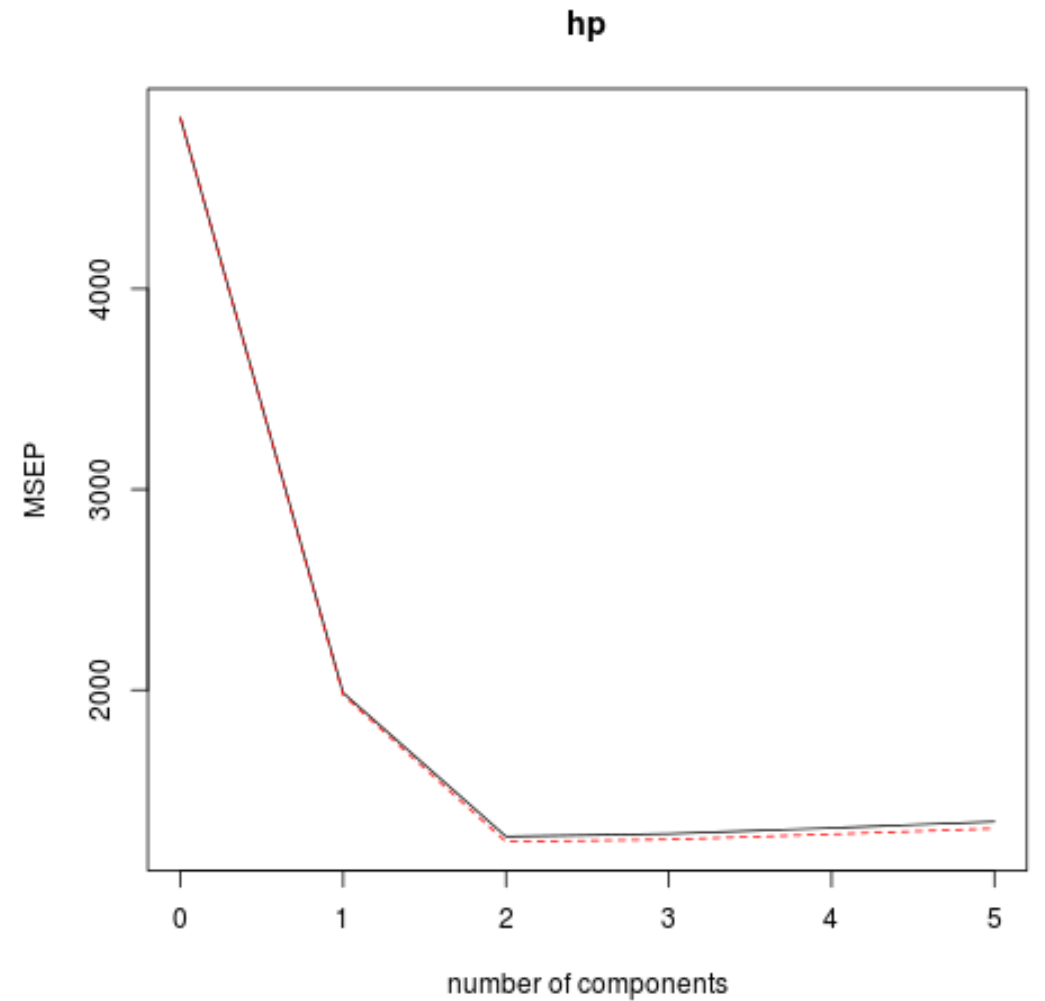
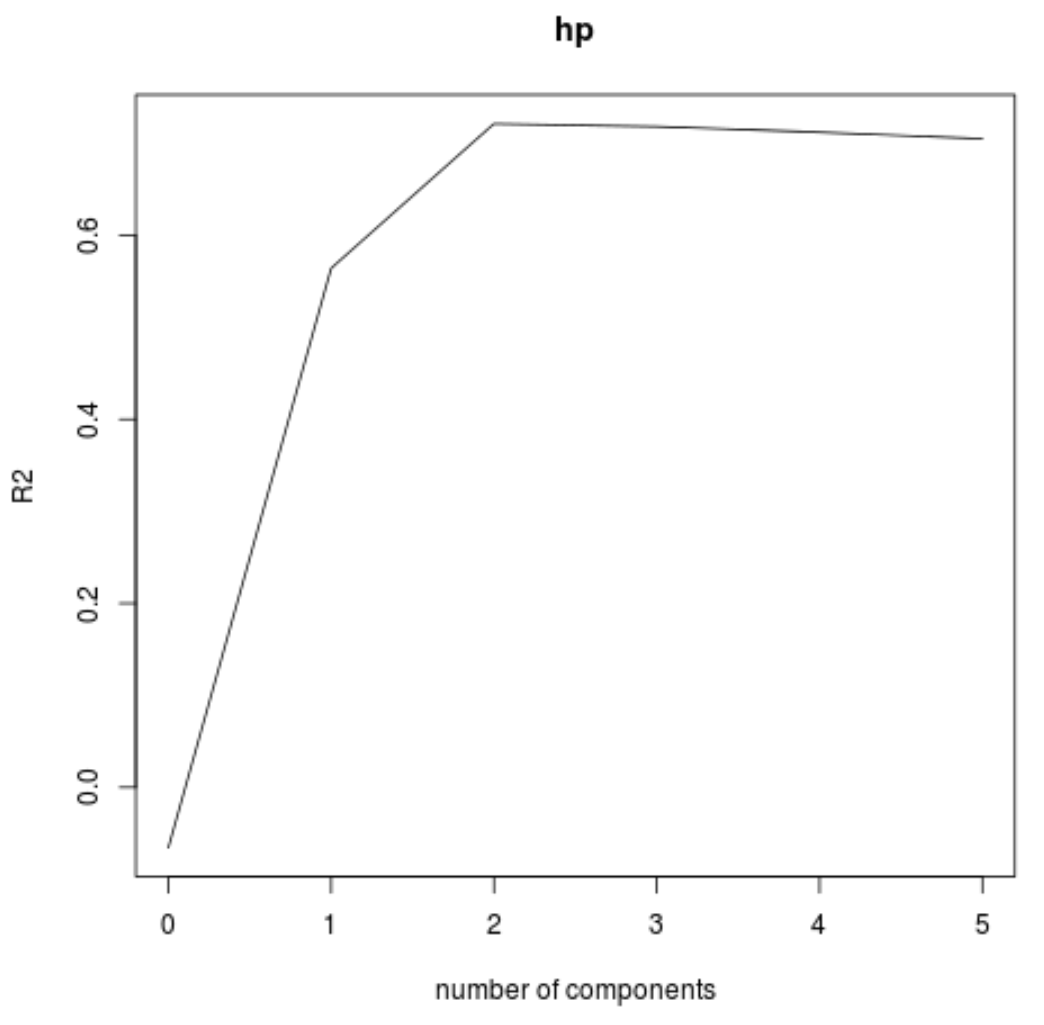
在每张图中,我们可以看到,通过添加两个主成分,模型拟合度有所提高,但当我们添加更多主成分时,模型拟合度往往会恶化。
因此,最优模型仅包含前两个主成分。
第 4 步:使用最终模型进行预测
我们可以使用最终的双主成分 PCR 模型来对新观察结果进行预测。
以下代码展示了如何将原始数据集拆分为训练集和测试集,并使用具有两个主成分的 PCR 模型对测试集进行预测。
#define training and testing sets train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")] y_test <- mtcars[26: nrow (mtcars), c("hp")] test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")] #use model to make predictions on a test set model <- pcr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ") pcr_pred <- predict(model, test, ncomp= 2 ) #calculate RMSE sqrt ( mean ((pcr_pred - y_test)^2)) [1] 56.86549
我们看到测试的 RMSE 结果为56.86549 。这是测试集观测值的预测hp值和观察到的hp值之间的平均偏差。
可以在此处找到此示例中 R 代码的完整用法。