如何在 r 中模拟和绘制二元正态分布

在统计学中，如果两个变量加在一起时呈正态分布，则它们遵循二元正态分布。

本教程介绍如何在 R 中执行以下任务：

• 模拟二元正态分布
• 使用等高线图（二维图）绘制二元正态分布
• 使用曲面图（3D 图）绘制二元正态分布

我们走吧！

示例 1：在 R 中模拟二元正态分布

在 R 中模拟二元正态分布的最简单方法是使用MASS包中的mvrnorm()函数。

下面的代码展示了如何在实践中使用该函数来模拟二元正态分布：

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

以下是mvrnorm()函数的每个参数的作用：

• n ：定义样本大小
• mu ：定义每个变量的平均值
• Sigma ：定义两个变量的协方差矩阵

最终结果是一个包含两个变量的数据框，两个变量加在一起时遵循正态分布。

示例 2：绘制二元正态分布

在 R 中绘制二元正态分布的最简单方法是使用mnormt()包中的函数。

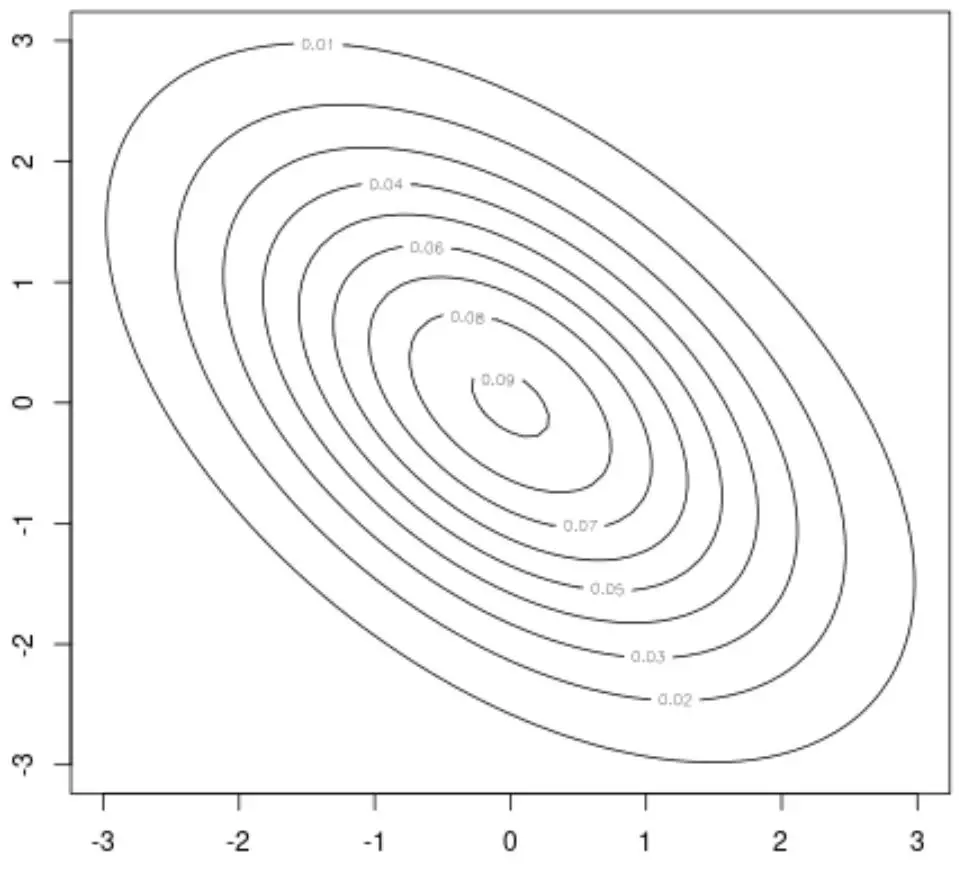
例如，我们可以使用此包的contour()函数来创建等高线图，它提供二元正态分布的二维可视化：

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

我们还可以使用persp()函数创建曲面图，它提供二元正态分布的 3D 可视化：

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

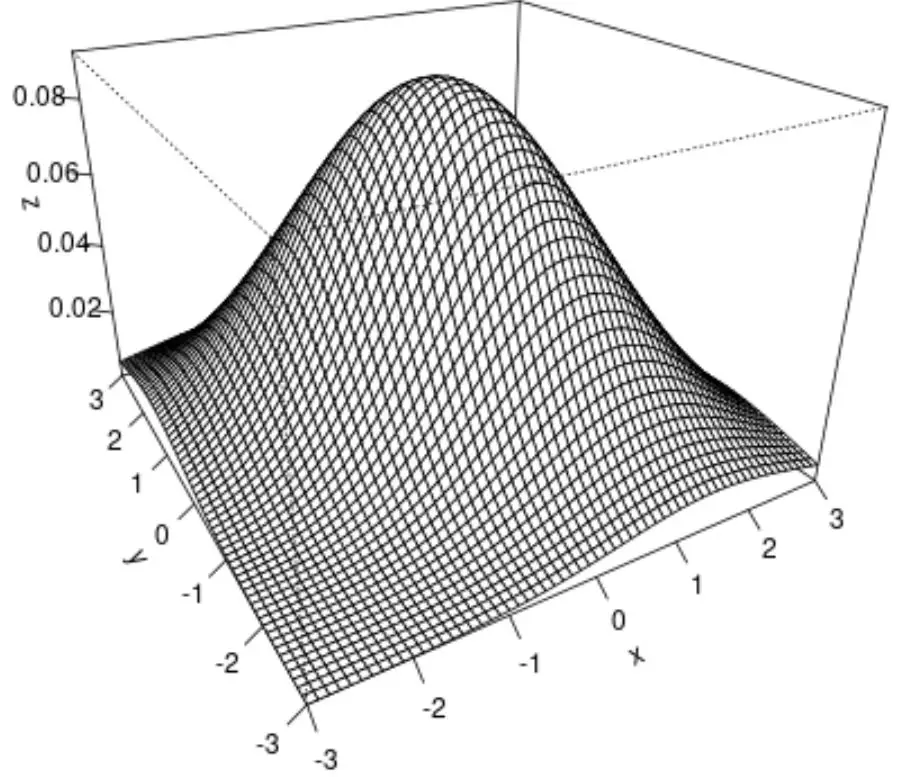
以下是persp()函数的每个参数的作用：

• theta, phi ：设置观察方向角度。
• Expand ：控制 z 轴的大小。
• ticktype ：控制轴上刻度线的外观。

最终结果是二元正态分布的 3D 曲面图。

其他资源

以下教程解释了如何在 R 中使用其他概率分布：

如何在R中使用正态分布
如何在 R 中使用二项式分布
如何在 R 中使用泊松分布
如何在 R 中使用多项式分布